1. Tập hợp các điểm biểu diễn của z thỏa\(\left| {z – 4} \right| + \left| {z + 4} \right| = 10\) là:
A. một elip có phương trình \(\dfrac{{{x^2}}}{{25}} + \dfrac{{{y^2}}}{{16}} = 1.\)
B. một elip có phương trình \(\dfrac{{{x^2}}}{9} + \dfrac{{{y^2}}}{{25}} = 1.\)
C. một elip có phương trình \(\dfrac{{{x^2}}}{{25}} + \dfrac{{{y^2}}}{9} = 1.\)
D. một elip có phương trình \(\dfrac{{{x^2}}}{{16}} + \dfrac{{{y^2}}}{{25}} = 1.\)
2. Phần ảo của số phức z = 2 + 3i là:
A. 2. B. 3.
C. 3i. D. 2i.
3. Trong không gian Oxyz cho 2 điểm A(-1;0;3), B(3;6;-7). Tọa độ của \(\overrightarrow {AB} \) là:
A. (-4;-6;10). B. (4;6;-10).
C. (2;3;-5). D. (-2;-3;5).
4. Cho số phức z có điểm biểu diễn trong mặt phẳng phức là M (như hình vẽ). Số phức \(\overline z \) là:
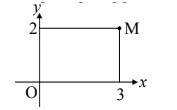
A. 3 + 2i. B. 3 – 2i.
C. 2 – 3i. D. – 2 + 3i.
5. Tập hợp các điểm biểu diễn số phức z thỏa \(\left| {z – 5 – 7i} \right| = 9\) là một đường tròn có tâm I và bán kính R. Kết quả nào sau đây là đúng?
A. I(5;7); R = 3.
B. I(-5;-7); R = 9.
C. I(5;-7); R = 9.
D. I(5;7); R = 9.
6. Trong không gian Oxyz cho tam giác MNP biết M(-9;0;4), N(3;6;-7) và G(-2;3;-1) là trọng tâm của tam giác MNP. Tọa độ điểm P là:
A. (0;-3;0). B. (0;2;0).
C. (0;3;1). D. (0;3;0).
7. Góc giữa hai véctơ \(\overrightarrow u = (1;2; – 1),\overrightarrow v = ( – 1; – 2;1)\) là:
A.\({180^ \circ }.\) B.\({135^ \circ }.\)
C.\({150^ \circ }.\) D.\({0^ \circ }.\)
8. Trong không gian Oxyz, mặt phẳng (Oxz) có phương trình là:
A. x = 0. B. z = 0.
C. y = 0. D. x + z = 0.
9. Hàm số nào sau đây không phải là nguyên hàm của hàm số g(x) = 2x + 2?
A.\(y = {(x – 1)^2}.\)
B.\(y = {x^2} + 2x + 2018.\)
C.\(y = {x^2} + 2x – 5.\)
D.\(y = {(x + 1)^2}.\)
10: Cho vật thể giới hạn bởi hai mặt phẳng x = 1, x = 3. Cắt vật thể đã cho bởi mặt phẳng vuông góc với trục Ox tại điểm có hoành độ bằng x, \(1 \le x \le 3\) ta được thiết diện có diện tích bằng \(3{x^2} + 2x.\)Thể tích của vật thể đã cho là:
A.\(V = 42\pi .\) B.\(V = 42.\)
C.\(V = 34.\) D.\(V = 34\pi .\)
11: Thể tích của khối tròn xoay sinh bởi hình phẳng giới hạn bởi các đường y = 3x, trục hoành, x = -1 khi quay quanh trục hoành là:
A.\(3\pi .\) B.\(12\pi .\)
C.\(\dfrac{{3\pi }}{2}.\) D.\(24\pi .\)
12: Giá trị của \(\int\limits_{\dfrac{1}{2}}^1 {\cos (\pi x).dx} \) là:
A.\(\dfrac{1}{\pi }.\) B.\(\dfrac{{31}}{{10}}.\)
C.\( – \dfrac{1}{\pi }.\) D. \( – \dfrac{{31}}{{10}}.\)
13: Cho số phức z = 2018 – 6i; w = x + yi \((x,y \in \mathbb{R}).\) Phần thực của z + 2w là:
A.2018 – 2x. B. 2018 + 2x.
C. – 6 – 2y. D. – 6 + 2y.
14: Cho số phức w = 2 + 5i. Điểm biểu diễn của số phức \((1 – i)\overline {\rm{w}} \) trong mặt phẳng Oxy là điểm nào trong các điểm sau?
A. (7;3). B. (7;-3).
C. (3;7). D. (-3;-7).
15: Trong không gian Oxyz cho \(\overrightarrow a = (2;2;1);\overrightarrow b = ( – 1;0;2).\) Khẳng định nào sau đâyy sai?
A.\(\left| {\overrightarrow b } \right| = 5.\) B.\(\overrightarrow a + \overrightarrow b = (1;2;3).\)
C.\(\left| {\overrightarrow a } \right| = 3.\) D. \(\overrightarrow a \bot \overrightarrow b .\)
16: Trong không gian Oxyz, cho đường thẳng \(d:\dfrac{{x – 2}}{1} = \dfrac{y}{{ – 2}} = \dfrac{z}{3}.\) Một vectơ chỉ phương của đường thẳng d là:
A.\(\overrightarrow u = (1;2;3).\)
B.\(\overrightarrow u = (1; – 2;3).\)
Advertisements (Quảng cáo)
C.\(\overrightarrow u = ( – 1; – 2; – 3).\)
D.\(\overrightarrow u = ( – 1;2;3).\)
17: Cho hàm số y = G(x) là một nguyên hàm của y = g(x) trên \(\left[ {a;b} \right]\). Mệnh đề nào sau đây đúng?
A.\(\int\limits_a^b {g(x)dx = G(b) – G(a).} \)
B. \(\int\limits_b^a {g(x)dx = g(b) – g(a).} \)
C. \(\int\limits_a^b {g(x)dx = G(a) – G(b).} \)
D.\(\int\limits_a^b {g(x)dx = g(b) – g(a).} \)
18: Diện tích hình phẳng giới hạn bởi các đường y = f(x), Ox, x = c, x = b (b > c) có công thức tính là:
A. \(S = \pi \int\limits_b^c {{{\left[ {f(x)} \right]}^2}} dx.\)
B. \(S = \pi \int\limits_b^c {\left| {f(x)} \right|} dx.\)
C. \(S = \pi \int\limits_c^b {\left| {f(x)} \right|} dx.\)
D.\(S = \int\limits_c^b {\left| {f(x)} \right|} dx.\)
19: Một ngyên hàm của \(f(x) = {3^x} + \dfrac{2}{x}\) là:
A. \(\dfrac{{{3^x}}}{{\ln 3}} – \dfrac{2}{{{x^2}}}.\)
B. \({3^x}.\ln 3 + 2\ln \left| x \right|.\)
C. \(\dfrac{{{3^x}}}{{\ln 3}} + \dfrac{2}{{{x^2}}}.\)
D. \(\dfrac{{{3^x}}}{{\ln 3}} + 2ln\left| x \right|.\)
20: Trong không gian Oxyz cho M(-2;4;6). Khi đó hình chiếu vuông góc của M trên mặt phẳng (Oyz) có tọa độ là:
A. (-2;0;6). B. (-2;4;0).
C. (0;4;6). D. (-2;0;0).
21: Phương trình mặt phẳng qua ba điểm A(0;0;3), B(0;2;0), C(1;0;0) trong không gian Oxyz là:
A. 6x + 3y + 2z + 6 = 0.
B. 6x + 3y + 2z – 6 = 0.
C. \(\dfrac{x}{1} + \dfrac{y}{2} + \dfrac{z}{3} = 0.\)
D. \(\dfrac{x}{3} + \dfrac{y}{2} + \dfrac{z}{1} = 1.\)
22: Cho \(\int\limits_0^{\ln 2} {f({e^{2x}}){e^{2x}}} dx = 40.\) Khi đó \(\int\limits_1^4 {f(x)dx} \) có giá trị là:
A. 20. B. 40.
C.10. D. 80.
23: Gọi \({z_1},{z_2}\) là hai nghiệm phức của phương trình \({z^2} – 2z + 2018 = 0.\) Khi đó kết quả của \(A = \left| {{z_1} + {z_2} – {z_1}.{z_2}} \right|\) là:
A. 2020. B. 2016.
C. 2021. D. 2017.
24: Diện tích hình phẳng giới hạn bởi \(y = {x^2} – 3x\) và y = x là:
A.\(\dfrac{{32}}{3}.\) B.\(\dfrac{5}{3}.\)
C.\(\dfrac{4}{3}.\) D.\(\dfrac{7}{3}.\)
25: Trong không gian Oxyz, biết đường thẳng\(d:\dfrac{{x + 1}}{2} = \dfrac{{y – 1}}{2} = z\) cắt mặt phẳng (P) x + 2y – z – 6 = 0 tại điểm M(a;b;c). Tính giá trị của K = a + b + c.
A. K = 9. B. K = -9.
Advertisements (Quảng cáo)
C. K = -5. D. K = 5.
26: Cho phương trình \({z^2} – az + b = 0,a,b \in R\) có một nghiệm z = 2 + i. Khi đó hiệu a – b bằng:
A. 9. B. – 9.
C. 1. D. -1.
27: Tập hợp các điểm biểu diễn cuae z thỏa \(\left| {\overline z – i} \right| = \left| {z + 2 – 3i} \right|\) là một đường thẳng có phương trình:
A. x – 2y + 3 = 0.
B. x – 2y -4 = 0.
C. x + 2y + 3 = 0.
D. x + 2y + 4 =0.
28: Diện tích hình phẳng giới hạn bởi y = f(x) và trục hoành (phần gạch sọc) trong hình vẽ có công thức là:
A.\(S = \left| {\int\limits_{ – 3}^1 {f(x)dx + \int\limits_1^2 {f(x)dx} } } \right|.\)
B.\(S = \int\limits_{ – 3}^1 {f(x)dx – \int\limits_1^2 {f(x)dx} } .\)
C.\(S = – \int\limits_{ – 3}^1 {f(x)dx + \int\limits_1^2 {f(x)dx} } .\)
D.\(S = \int\limits_{ – 3}^1 {f(x)dx + \int\limits_1^2 {f(x)dx} } .\)
29: Trong không gian Oxyz, phương trình mặt cầu (S0 có tâm I(3;-4;5) và tiếp xúc với mặt phẳng (Oxz) là:
A.\({(x + 3)^2} + {(y – 4)^2} + {(z + 5)^2} = 16.\)
B.\({(x – 3)^2} + {(y + 4)^2} + {(z + 5)^2} = 25.\)
C.\({(x – 3)^2} + {(y + 4)^2} + {(z – 5)^2} = 16.\)
D.\({(x – 3)^2} + {(y + 4)^2} + {(z – 5)^2} = 9.\)
30: Cho z = a + bi \((a,b \in \mathbb{R})\). Mệnh đề nào sau đây là sai:
A.\(\overline z + z = 2a.\)
B.\(\left| z \right| = \left| {\overline z } \right|.\)
C.\(z.\overline z = {\left| z \right|^2}.\)
D.\(z – \overline z = – 2bi.\)
31: Trong không gian Oxyz, khoảng cách giữa hai mặt phẳng (P): x – 2y – 2z + 6 = 0 và (Q): 2x – 4y – 4z – 2 = 0 là:
A.2. B. 1.
C.\(\dfrac{7}{3}.\) D.\(\dfrac{5}{3}.\)
32: Trong không gian Oxyz cho mặt cầu \((S):{x^2} + {y^2} + {z^2} – 2x + 4z + 1 = 0.\) Mệnh đề nào sau đây đúng?
A.(S) có tâm I(1;-2;0), bán kính R = 2.
B. (S) có tâm I(1;0;-2), bán kính R = 2.
C. (S0 đi qua điểm M(-1;0;0).
D. Điểm O nằm bên trong mặt cầu (S).
33: Cho 2 số phức \({z_1} = 1 + i;{z_2} = 2 – m.i,m \in \mathbb{R}.\) Tìm m để \({z_1}.{z_2}\) là một số thuần ảo.
A. m = -2. B. m = 2.
C. m = -1. D. m = 1.
34: Trong không gian Oxyz, biết mặt phẳng (P): x + 2y + 2y – 2z – 2 = 0 cắt mặt cầu \((S):{(x – 1)^2} + {(y – 2)^2} + {z^2} = 5\) theo giao tuyến là một đường tròn. Tính diện tích của đường tròn giao tuyến.
A.\(4\pi .\) B.\(9\pi .\)
C.\(3\pi .\) D.\(\dfrac{{3\pi }}{2}.\)
35: Cho \(\int\limits_1^2 {\ln x.dx} = a\ln 2 – b(a,b \in \mathbb{Z})\). Khi đó a + 2b thuộc khoảng nào sau đây?
A. (-1;1). B. (1;2).
C. (-2;-1). D. (3;5).
36: Cho số phức z = a +bi,\((a,b \in \mathbb{R})\) thỏa \((2z – 1)(1 + i) – (\overline z + 3i)(1 – i) \)\(\,= 3 – 7i.\) Tính \(P = {a^2} + b.\)
A. 2. B. 13.
C. 7. D. 5.
37: Cho hai đường thẳng \({d_1}:\left\{ \begin{array}{l}x = 1 + t\\y = 2 – t\\z = 3 + 2t\end{array} \right.\) và \({d_2}:\dfrac{{x – 1}}{2} = \dfrac{{y – m}}{1} = \dfrac{{z + 2}}{{ – 1}}(m \in \mathbb{R})\) . Tìm giá trị của tham số m để \({d_1}\) và \({d_2}\) cắt nhau.
A. m = 5. B. m = 4.
C. m = 9. D. m = 7.
38: Trong không gian Oxyz, cho hai đường thẳng \({d_1}:\dfrac{{x – 2}}{1} = \dfrac{{y – 1}}{{ – 1}} = \dfrac{{z – 2}}{{ – 1}};\) \({d_2}:\left\{ \begin{array}{l}x = 3 + t\\y = 2 + t\\z = 5\end{array} \right.\). Biết đường vuông góc chung của \({d_1},{d_2}\) cắt \({d_1}\) tại A(a;b;c), tính tổng S = a + b + c.
A. 2. B. 5.
C. 4. D. 8.
39: Trong không gian Oxyz cho mặt cầu (S): \({x^2} + {y^2} + {z^2} – 2z – 3 = 0\) và mặt phẳng (P); 2x – y – 2z + 8 = 0. Tiếp diện của mặt cầu (S) song song với (P) cắt Ox, Oy, Oz lần lượt tại các điểm A, B và C. Tính thể tích tứ diện OABC.
A.\(\dfrac{8}{3}.\) B. \(\dfrac{{15}}{6}.\)
C.\(\dfrac{{64}}{3}.\) D. \(\dfrac{7}{6}.\)
40: Cho \(\int\limits_0^4 {{e^{\sqrt x }}} dx = a.{e^2} + b(a,b \in \mathbb{Z}).\) Khi đó \(S = {a^2} + {b^3}\) là:
A. 14. B. 8.
C. 12. D. -4.
41: Cho số phức z thỏa \(\left| {z + 3 – 4i} \right| = 4.\) Giá trị tuyệt đối của \(\left| z \right|\) là:
A. 7. B. \(4 + \sqrt 5 .\)
C. 8. D. 9.
42: Cho (H) là hình tam giác (phần gạch sọc). Gọi V là thể tích của khối nón tròn xoay tạo thành khi quay (H) quanh trục Ox. Tìm m để \(V = 36\pi .\)

A. 4. B. 5.
C. 3. D. 6.
43: Trong không gian với hệ tọa độ Oxyz, cho điểm M(2;5;-4) và mặt phẳng (P): x + y – 3z + 3 = 0. Gọi H là hình chiếu vuông góc của M trên mặt phẳng (P). Khi đó cao độ của điểm H là:
A. 4. B. 5.
C. 3. D. 6.
44: Cho số phức w có phần thực bằng 2 lần phần ảo và \(\left| {\rm{w}} \right| = 2\sqrt 5 .\) Tính \(\left| {{\rm{w – 3 + i}}} \right|\) biết phần ảo của w là số âm.
A.\(\sqrt {10} .\) B.\(5\sqrt 2 .\)
C.\(2\sqrt 5 .\) D. \(\sqrt 2 .\)
45: Trong không gian Oxyz, cho điểm H(6;1;1) và 2 đường thẳng \({d_1}:\dfrac{{x – 1}}{2} = \dfrac{{y + 1}}{2} = \dfrac{z}{1};\) \({d_2}:\left\{ \begin{array}{l}x = 2\\y = t\\z = – 1 + t\end{array} \right..\) Gọi (P) là mặt phẳng chứa \({d_1}\) và song song với \({d_2}.\) Khi đó khoảng cách từ H đến (P) bằng:
A. 4. B. 2.
C. 1. D. 3.
46: Cho số phức w thỏa \(\left| {{\rm{w}} – 2i} \right| = \left| {\overline {\rm{w}} + 3 – i} \right|\). Tính giá trị nhỏ nhất của \(T = \left| {{\rm{(1 + i)w + 4 + 6}}i} \right|.\)
A.\(\dfrac{{5\sqrt 2 }}{2}.\) B. 3.
C.\(\dfrac{{3\sqrt 2 }}{2}.\) D. 5.
47: Một hình vuông có cạnh bằng 2b cm (b > 0). Người ta đã sử dụng bốn đường parabol có chung đỉnh tại tâm của hình vuông để tạo ra một bông hoa 4 cánh (được tô đậm như hình vẽ). Tìm b để diện tích của bông hoa bằng \(4800c{m^2}.\)
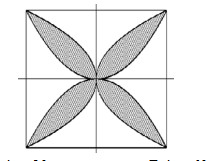
A. b = 30 cm. B. b = 60 cm.
C. b = 40 cm. D. b = 80 cm.
48: Trong không gian với hệ tọa độ Oxyz, cho hai điểm A(10;6;-2), B(5;10;-9) và mặt phẳng \((\alpha ):2x + 2y + z – 12 = 0.\) Điểm M di động trên mặt phẳng \((\alpha )\) sao cho MA, MB luôn tạo với \((\alpha )\) các góc bằng nhau. Biết M luôn thuộc một đường tròn (C) cố định. Cao độ của tâm đường tròn (C) là:
A. – 12. B. – 9.
C. 2. D. 10.
49: Trong không gian với hệ tọa độ Oxyz, cho (P) là mặt phẳng chứa đường thẳng \(d:\dfrac{{x – 4}}{3} = \dfrac{y}{1} = \dfrac{{z + 4}}{{ – 4}}\) và tiếp xúc với mặt cầu \((S):\)\(\,{(x – 3)^2} + {(y + 3)^2} + {(z – 1)^2} = 9.\) Khi đó mặt phẳng (P) cắt trục Oz tại điểm nào trong các điểm sau?
A.B(0;0;2). B. D(0;0;-2).
C. C(0;0;-4). D. A(0;0;4).
50: Cho f(x) là hàm số liên tục trên R và thỏa \(f({x^2} + 3x + 1) = x + 2.\) Tính \(\int\limits_1^5 {f(x)dx.} \)
A.\(\dfrac{{37}}{6}.\) B.\(\dfrac{{527}}{3}.\)
C.\(\dfrac{{61}}{6}.\) D.\(\dfrac{{464}}{3}.\)

|
1 |
2 |
3 |
4 |
5 |
|
C |
B |
B |
B |
D |
|
6 |
7 |
8 |
9 |
10 |
|
A |
C |
C |
A |
C |
|
11 |
12 |
13 |
14 |
15 |
|
A |
C |
B |
D |
A |
|
16 |
17 |
18 |
19 |
20 |
|
B |
A |
D |
D |
C |
|
21 |
22 |
23 |
24 |
25 |
|
B |
D |
B |
A |
D |
|
26 |
27 |
28 |
29 |
30 |
|
D |
A |
C |
C |
D |
|
31 |
32 |
33 |
34 |
35 |
|
C |
B |
A |
A |
D |
|
36 |
37 |
38 |
39 |
40 |
|
D |
A |
B |
A |
C |
|
41 |
42 |
43 |
44 |
45 |
|
D |
C |
C |
B |
C |
|
46 |
47 |
48 |
49 |
50 |
|
D |
B |
A |
D |
C |