1. Tìm phần ảo của số phức \(z = \dfrac{3}{i}.\)
A. – 1. B. 1.
C. – 3. D. 3.
2. Trong không gian Oxyz, cho mặt phẳng (P): \(x – 2y + 5z – 4 = 0\). Điểm nào sau đây thuộc mặt phẳng (P)?
A. \(A(0;0;4).\) B. \(B(-1;2;3).\)
C. \(C(1;-2;5).\) D. \(D(-5;-2;1).\)
3. Tập nghiệm của phương trình \({x^2} + 9 = 0\) trên tập số phức là:
A.\(\emptyset .\) B.\(\left\{ { – 3;\left. 3 \right\}} \right..\)
C.\(\left\{ {0;\left. 3 \right\}} \right..\) D.\(\left\{ { – 3i;\left. {3i} \right\}} \right..\)
4. Trong không gian Oxyz, cho đường thẳng d: \(\dfrac{{x – 2}}{1} = \dfrac{{y + 1}}{{ – 3}} = \dfrac{{z – 3}}{{ – 2}}.\) Vectơ nào sau đây là một vectơ chỉ phương của d?
A.\(\overrightarrow u (1;3; – 2).\)
B.\(\overrightarrow u ( – 1;3;2).\)
C.\(\overrightarrow u (2; – 1;3).\)
D.\(\overrightarrow u ( – 2;1; – 3).\)
5. Họ nguyên hàm của hàm số f(x) = sinx là:
A. sinx + C. B. cosx + C.
C. – sinx + C. D. – cosx + C.
6. Trong không gian Oxyz, cho mặt cầu \((S) :{(x + 1)^2} + {y^2} + {(z – 3)^2} = 4.\) Tìm tọa độ tâm I và bán kính r của mặt cầu (S).
A. \(I(1;0;-3), r = 4.\)
B. \(I(-1;0;3), r = 2.\)
C. \(I(-1;0;3), r = 4.\)
D. \(I(1;0;-3), r = 2.\)
7. Điểm biểu diễn số phức \(z = 2 – 3i\) trên mặt phẳng Oxy là điểm có tọa độ:
A. \((-2;3).\) B. \((-3;2).\)
C. \((2;3).\) D. \((2;-3).\)
8. Họ nguyên hàm của hàm số \(f(x) = {e^x}\) là:
A.\(\ln \left| x \right| + C.\) B.\( – {e^x} + C.\)
C.\({e^x} + C.\) D.\(\dfrac{1}{x} + C.\)
9. Tính \(I = \int\limits_{ – 1}^2 {6{x^2}} dx.\)
A. I = 18. B. I = 22.
C. I = 26. D. I = 14.
10: Trong không gian Oxyz, cho mặt phẳng (P): \(4x – y – 3z + 7 = 0.\) Vectơ nào dưới đây là một vectơ pháp tuyến của (P)?
A.\(\overrightarrow n (4; – 1;3).\)
B.\(\overrightarrow n ( – 4; – 1;3).\)
C. \(\overrightarrow n (4; – 3;7).\)
D. \(\overrightarrow n (4; – 1; – 3).\)
11: Số phức liên hợp của số phức \(z = \dfrac{2}{{1 + i}}\) là:
A.\(\dfrac{{ – 2}}{{1 – i}}.\) B. 1 – i.
C.\(\dfrac{{ – 2}}{{1 + i}}.\) D. 1 + i.
12: Trong không gian Oxyz, cho hai điểm A(2;-1;3) và B(3;1;2). Tọa độ của vectơ \(\overrightarrow {AB} \) là:
A. (1;0;-1). B. (1;-2;-1).
C. (1;2;-1). D. (-1;-2;1).
13: Họ nguyên hàm của hàm số f(x) = 2x + 1 là:
A.\({x^2} + x + C.\) B.\({x^2} + 1 + C.\)
C.\(2{x^2} + 1 + C.\) D.\(4{x^2} + x + C.\)
14: Tính \(I = \int\limits_0^1 {{e^x}} dx.\)
A.\(I = {e^2} – e.\) B.\(I = e – 1.\)
C.\(I = 1 – e.\) D.\(I = e.\)
15: Biết \(\int\limits_1^5 {\dfrac{1}{{2x – 1}}} dx = \ln a.\) Tính a.
A. a = 8. B. a = 3.
C. a = 9. D. a = 81.
16: Trong không gian Oxyz, cho mặt phẳng \((\alpha ):2x – y + 3z + 4 = 0\) và điểm A(2;-1;2). Mặt phẳng qua A song song với trục Oy và vuông góc với \((\alpha )\) có phương trình là:
A. \(– 3x – 2z + 10 = 0.\)
B. \(3y – 2z – 2 = 0.\)
C. \(3x – 2z – 2 = 0.\)
D. \(3x – 2y – 8 = 0.\)
17: Cho hàm số f(x) liên tục trên đoạn \(\left[ {0;2017} \right]\) và có một nguyên hàm là F(x)= 2x + 2018. Tính \(I = \int\limits_0^{2017} {f(x)dx} .\)
A. I = 6052. B. I = 4068289.
C. I = 8138595. D. I = 4034.
18: Gọi \({z_1},{z_2}\) là các nghiệm phức của phương trình \(5{z^2} – 7z + 11 = 0.\) Tính \(T = \left| {{z_1} – {z_2}} \right|.\)
Advertisements (Quảng cáo)
A.\(\dfrac{{3\sqrt {19} }}{5}.\) B.\(\dfrac{{171}}{{25}}.\)
C. \(\dfrac{7}{5}.\) D.\(\dfrac{{11}}{5}.\)
19: Trong không gian Oxyz, cho hai điểm M(1;0;-2) và N(4;3;0). Tính độ dài đoạn thẳng NM.
A.\(MN = \sqrt {14} .\) B. \(MN = (3;3;2).\)
C.\(NM = \sqrt {22} .\) D. \(NM = (-3;-3;2).\)
20: Trong không gian Oxyz, cho đường thẳng \(d:\dfrac{{x – 1}}{1} = \dfrac{{y – 3}}{{ – 2}} = \dfrac{{z + 4}}{1}.\) Phương trình nào dưới đây là phương trình của đường thẳng đi qua điểm M(1;-3;6) và somg song với d?
A. \(\dfrac{{x – 1}}{1} = \dfrac{{y + 3}}{3} = \dfrac{{z – 6}}{{ – 4}}.\)
B. \(\dfrac{{x – 1}}{1} = \dfrac{{y + 3}}{3} = \dfrac{{z + 4}}{6}.\)
C. \(\dfrac{{x – 1}}{1} = \dfrac{{y – 3}}{{ – 2}} = \dfrac{{z + 6}}{1}.\)
D. \(\dfrac{{x – 1}}{1} = \dfrac{{y + 3}}{{ – 2}} = \dfrac{{z – 6}}{1}.\)
21: Trong không gian Oxyz, cho hai vectơ \(\overrightarrow u = (1; – 3;6)\) và \(\overrightarrow v = (1;3;0)\). Tính \(\overrightarrow u .\overrightarrow v .\)
A. (1;-3;4). B. – 8.
C. – 5. D. (1;-9;0).
2.2: Cho số phức z = 2 +bi. Tính \(z.\overline z .\)
A. \(z.\overline z = \sqrt {4 + {b^2}} .\)
B. \(z.\overline z = 4 – {b^2}.\)
C. \(z.\overline z = – b.\)
D. \(z.\overline z = 4 + {b^2}.\)
23: Diện tích của hình phẳng giới hạn bởi đồ thị của hàm số \(y = {x^3} – 3x + 2\) và đường thẳng y = x + 2 bằng:
A. 12. B. 0.
C. 8. D. 6.
24: Tính \(I = \int\limits_1^4 {({x^2}} + 3\sqrt x )dx\)
A. I = 34. B. I = 36.
C. I = 35. D. I = 37.
25: Cho \(\int\limits_1^5 {f(x)dx = a} \) và \(\int\limits_1^{2018} {f(x)dx = b} \). Khi đó \(\int\limits_5^{2018} {f(x)dx} \) bằng:
A. b – a. B. – a – b.
C. a – b. D. a + b.
26: Trong không gian Oxyz, cho A(1;-2;1) và B(0;1;3). Phương trình đường thẳng qua hai điểm A, B là:
A. \(\dfrac{{x + 1}}{{ – 1}} = \dfrac{{y – 3}}{{ – 2}} = \dfrac{{z – 2}}{1}.\)
B. \(\dfrac{x}{{ – 1}} = \dfrac{{y – 1}}{{ – 2}} = \dfrac{{z – 3}}{2}.\)
C. \(\dfrac{{x + 1}}{{ – 1}} = \dfrac{{y – 2}}{3} = \dfrac{{z + 1}}{2}.\)
D. \(\dfrac{x}{1} = \dfrac{{y – 1}}{{ – 2}} = \dfrac{{z – 3}}{1}.\)
27: Cho số phức z có điểm biểu diễn trong mặt phẳng tọa độ Oxy là điểm M(-1;5). Tính môđun của z.
A.\(\left| z \right| = \sqrt {26} .\) B.\(\left| z \right| = 4.\)
C.\(\left| z \right| = 2.\) D.\(\left| z \right| = \sqrt {24} .\)
28: Họ nguyên hàm của hàm số f(x) = 4xlnx là:
A.\({x^2}(2{\mathop{\rm lnx}\nolimits} + 1) + C.\)
B.\(4{x^2}(2{\mathop{\rm lnx}\nolimits} – 1) + C.\)
Advertisements (Quảng cáo)
C. \({x^2}(2{\mathop{\rm lnx}\nolimits} – 1) + C.\)
D.\({x^2}(8{\mathop{\rm lnx}\nolimits} – 16) + C.\)
29: Đặt \(A = \int {{{\cos }^2}} xdx,B = \int {{{\sin }^2}} xdx.\) Xác định A – B.
A. \(A – B = – \dfrac{1}{2}\sin 2x + C.\)
B. \(A – B = – \cos 2x + C.\)
C. \(A – B = – 2\cos 2x + C.\)
D. \(A – B = \dfrac{1}{2}\sin 2x + C.\)
30: Trong không gian Oxyz, phương trình mặt cầu tâm I(3;-1;4) và đi qua điểm M(1;-1;2) là:
A. \({(x – 3)^2} + {(y + 1)^2} + {(z – 4)^2} = 4.\)
B. \({(x + 3)^2} + {(y – 1)^2} + {(z + 4)^2} = 8.\)
C. \({(x – 1)^2} + {(y + 1)^2} + {(z – 2)^2} = 2\sqrt 2 .\)
D. \({(x – 3)^2} + {(y + 1)^2} + {(z – 4)^2} = 8.\)
31: Xác định f(x) biết \(\int {f(x)dx = \dfrac{1}{x}} + {e^x} + C.\)
A. \(f(x) = \ln \left| x \right| + {e^x} + C.\)
B. \(f(x) = \dfrac{1}{{{x^2}}} + {e^x} + C.\)
C. \(f(x) = – \dfrac{1}{{{x^2}}} + {e^x}.\)
D. \(f(x) = \ln \left| x \right| + {e^x}.\)
32: Gị S là diện tích của hình phẳng giới hạn bởi các đường \(y = {x^2}\)và \(y = 2 – {x^2}\). Đẳng thức nào sau đây đúng?
A. \(S = 2\int\limits_0^1 {\left| {1 – {x^2}} \right|} dx.\)
B. \(S = 2\int\limits_{ – 1}^1 {(1 – {x^2})} dx.\)
C. \(S = 2\int\limits_0^1 {({x^2} – 1)} dx.\)
D. \(S = 2\int\limits_{ – 1}^1 {({x^2} – 1)} dx.\)
33: Tổng phần thực và phần ảo của số phức \(z = \dfrac{{1 + 5i}}{{2i}}\) bằng
A. 3. B. -2.
C. 2. D. – 3,
34: Trong không gian Oxyz, cho mặt phẳng \((\alpha ):3x – 2y + 4z + 4 = 0\) và điểm M(4;-1;2). Phương trình nào sau đây là phương trình của đường thẳng qua M và vuông góc với mặt phẳng \((\alpha )?\)
A. \(\dfrac{{x + 3}}{4} = \dfrac{{y – 2}}{{ – 1}} = \dfrac{{z + 4}}{2}.\)
B. \(\dfrac{{x + 4}}{3} = \dfrac{{y – 1}}{{ – 2}} = \dfrac{{z + 2}}{4}.\)
C. \(\dfrac{{x – 4}}{3} = \dfrac{{y + 1}}{{ – 2}} = \dfrac{{z – 2}}{4}.\)
D. \(\dfrac{{x – 3}}{4} = \dfrac{{y + 2}}{{ – 1}} = \dfrac{{z – 4}}{2}.\)
35: Trong không gian Oxyz, mặt phẳng đi qua M(1;2;3) và song song với mặt phẳng \(x + 2y – 3z + 1 = 0\) có phương trình là:
A. \(x + 2y – 3z + 2 = 0.\)
B. \(x + 2y – 3z + 5 = 0. \)
C. \(x + 2y – 3z + 4 = 0.\)
D. \(x + 2y – 3z + 3 = 0. \)
36:Cho \(\int\limits_1^e {\dfrac{{\ln x}}{{{x^2}}}dx} = \dfrac{{a.e + b}}{e}.\) Tìm \(S = a + b.\)
A. S = -1. B. S = -3.
C. S = 1. D. S = 3.
37: Họ nguyên hàm của hàm số \(f(x) = \dfrac{{98}}{{{{(2x + 1)}^{50}}}}\) là:
A. \( – \dfrac{1}{{{{(2x + 1)}^{49}}}} + C.\)
B. \( – \dfrac{2}{{{{(2x + 1)}^{49}}}} + C.\)
C. \(\dfrac{2}{{51{{(2x + 1)}^{51}}}} + C.\)
D. \(\dfrac{2}{{{{(2x + 1)}^{51}}}} + C.\)
38: Gọi \({z_1},{z_2},{z_3},{z_4}\) là các nghiệm phức của phương trình \({z^4} + {z^2} – 6 = 0.\) Tính \(T = z_1^2 + z_2^2 + z_3^2 + z_4^2.\)
A. T = 2. B. T = 14.
C. T = 4. C. T = -2.
39: Các điểm biểu diễn số phức z thỏa mãn \(z.\overline z + 3(z – \overline z ) = 5 + 12i\) thuộc đường nào trong các đường cho bởi phương trình sau đây?
A. \(y = 2{x^2}.\) B. \({(x – 1)^2} + {y^2} = 5.\)
C. y = 2x. D. y = -2x.
40: Trong không gian Oxyz, cho mặt cầu (S) có tâm I(1;0;-5) bán kính r = 4 và điểm m(1;3;-1). Các đường thẳng qua M tiếp xúc với (S) tại các tiếp điểm thuộc đường tròn có bán kính R bằng bao nhiêu?
A. \(R = \dfrac{{12}}{5}.\)
B. \(R = \dfrac{{3\sqrt 5 }}{5}.\)
C. R = 3.
D.\(R = \dfrac{5}{2}.\)
41: Trong không gian Oxyz, cho hai đường thẳng \({d_1}:\dfrac{{x – 1}}{2} = \dfrac{{y + 1}}{3} = \dfrac{{z – 3}}{{ – 5}}\) và \({d_2}:\left\{ \begin{array}{l}x = – 1 + t\\y = 4 + 3t\\z = 1 + t\end{array} \right..\) Phương trình mặt phẳng chứa đường thẳng \({d_1}\) và song song với đường thẳng \({d_2}\) là:
A. 18x + 7y + 3z + 20 = 0.
B. 18x – 7y + 3z + 34 = 0.
C. 18x + 7y + 3z – 20 = 0.
D. 18x – 7y + 3z – 34 = 0.
42: Cho số phức z có điểm biểu diễn trong mặt phẳng tọa độ Oxy là điểm M(1;-2). Tính môđun của số phức \({\rm{w}} = i\overline z – {z^2}.\)
A. \(\sqrt 6 .\) B. \(\sqrt {26} .\)
C. 26. D. 6.
43: Trong không gian Oxyz, cho hai mặt phẳng (P): 7x + 3ky +mz + 2 = 0 và (Q): kx – my + z + 5 = 0. Khi giao tuyến của (P) và (Q) vuông góc với mặt phẳng \((\alpha );x – y – 2z – 5 = 0\) hãy tính \(T = {m^2} + {k^2}.\)
A. T = 10. B. T = 2.
C. T = 8. D. T = 18.
44: Trong không gian Oxyz, cho đường thẳng \(d:\dfrac{{x – 1}}{2} = \dfrac{{y + 3}}{{ – 1}} = \dfrac{{z – 5}}{3}.\) Viết phương trình mặt cầu có tâm I(5;1;-1) và tiếp xúc với d.
A. \({(x – 5)^2} + {(y – 1)^2} + {(z + 1)^2} = 56.\)
B. \({(x – 5)^2} + {(y – 1)^2} + {(z + 1)^2} = 56.\)
C. \({(x – 5)^2} + {(y – 1)^2} + {(z + 1)^2} = \sqrt {56} .\)
D. \({(x – 5)^2} + {(y – 1)^2} + {(z + 1)^2} = 110.\)
45: Gọi (H) là hình phẳng giới hạn bởi các đường \(y = {x^2} – 3x,y = 0.\) Tính thể tích khối tròn xoay được tạo thành khi quay hình (H) quanh trục hoành.
A. \(\dfrac{{81\pi }}{{10}}.\) B. \(\dfrac{{85\pi }}{{10}}.\)
C. \(\dfrac{{81}}{{10}}.\) D. \(\dfrac{{41\pi }}{{10}}.\)
46: Tập hợp các điểm biểu diễn số phức z trong mặt phẳng tọa độ Oxy là đường thẳng có phương trình \(\sqrt 3 x – y – 2018 = 0.\) Tìm giá trị nhỏ nhất của \(P = \left| {z – 2\sqrt 3 + 2i} \right|\)
A. \(\min P = \dfrac{{1005\sqrt 2 }}{2}.\)
B. \(\min P = \dfrac{{1013\sqrt 3 }}{3}.\)
C. \(\min P = 1013.\)
D. \(\min P = 1005.\)
47: Tính thể tích của khối tròn xoay được tạo thành khi quay hình phẳng (H) (phần tô màu đen trong hình bên) quanh trục Ox.
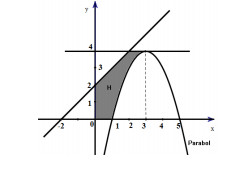
A. \(\dfrac{{61\pi }}{{15}}.\) B. \(\dfrac{{88\pi }}{5}.\)
C. \(\dfrac{{8\pi }}{5}.\) D. \(\dfrac{{424\pi }}{{15}}.\)
48: Cho hàm số f(x) liên tục trên \(\left[ {0;1} \right]\) thỏa mãn \(3xf({x^2}) – f(x) = 9{x^3} – 1.\) Tính \(\int\limits_0^1 {f(x)dx.} \)
A. \(\dfrac{5}{2}.\) B. \(\dfrac{5}{4}.\)
C. \(\dfrac{1}{4}.\) D. \(\dfrac{1}{8}.\)
49: Trong không gian Oxyz, cho mặt cầu (S) có phương trình \({x^2} + {y^2} + {z^2} – 2x + 2y + 1 = 0.\) Viết phương trình (P) đi qua hai điểm A(0;-1;1), B(1;-2;1) đồng thời cắt mặt cầu (S) theo giao tuyến là đường tròn có chu vi bằng \(\sqrt 2 \pi .\)
A. x + y + 3z – 2 = 0, x + y – 5z + 6 = 0.
B. x + y + 3z – 2 = 0, x + y + z = 0.
C. x + y – 3z + 4 = 0, x + y – z + 2 = 0.
D. x + y + 1 = 0, x + y + 4z – 3= 0.
50: Trong không gian Oxyz, cho mặt cầu \((S):{x^2} + {y^2} + {z^2} – 4y – 4z – 7 = 0.\) Gọi M(a;b;c) là điểm thuộc (S) sao cho \(2a + 3b + 6c\) đạt giá trị lớn nhất. Tính \(T = a + b + c.\)
A. \(T = \dfrac{{81}}{7}.\)
B. \(T = – \dfrac{{12}}{7}.\)
C. \(T = \dfrac{{11}}{7}.\)
D. \(T = \dfrac{{79}}{7}.\)

|
1 |
2 |
3 |
4 |
5 |
|
C |
D |
D |
B |
D |
|
6 |
7 |
8 |
9 |
10 |
|
B |
D |
C |
A |
D |
|
11 |
12 |
13 |
14 |
15 |
|
D |
C |
A |
B |
B |
|
16 |
17 |
18 |
19 |
20 |
|
C |
D |
A |
C |
D |
|
21 |
22 |
23 |
24 |
25 |
|
B |
D |
C |
C |
A |
|
26 |
27 |
28 |
29 |
30 |
|
B |
A |
C |
D |
D |
|
31 |
32 |
33 |
34 |
35 |
|
C |
B |
C |
C |
C |
|
36 |
37 |
38 |
39 |
40 |
|
A |
A |
D |
A |
A |
|
41 |
42 |
43 |
44 |
45 |
|
D |
B |
A |
B |
A |
|
46 |
47 |
48 |
49 |
50 |
|
D |
B |
A |
D |
D |