1. Trong các dãy số sau, dãy số nào có giới hạn bằng \( + \infty \) ?
A. \({u_n} = \dfrac{{{{\left( {3 – 2n} \right)}^3}}}{{{{\left( {1 – n} \right)}^2}}}\)
B. \({u_n} = \dfrac{{{{\left( {1 – 2n} \right)}^2}.n}}{{2n – 1}}\)
C. \({u_n} = \dfrac{{{{\left( {1 + 2n} \right)}^4}}}{{{{\left( {1 + 7n} \right)}^2}.{n^3}}}\)
D. \({u_n} = \dfrac{{\left( {2n – 1} \right).{n^4}}}{{{{\left( {1 – n} \right)}^3}}}\)
2. \(\lim \dfrac{{{3^n} – 1}}{{{2^n} – {{2.3}^n} + 1}}\) bằng:
A. \( – \dfrac{1}{2}\) B. \(\dfrac{3}{2}\)
C. \(\dfrac{1}{2}\) D. \( – 1\)
3. Cho dãy số \({S_n} = \dfrac{1}{3} + \dfrac{1}{{{3^2}}} + … + \dfrac{1}{{{3^n}}}\) . Giới hạn \(\lim {S_n}\) bằng:
A. \(\dfrac{1}{2}\) B. \(\dfrac{3}{2}\)
C. \(\dfrac{5}{3}\) D. \(\dfrac{4}{3}\)
4. Tính \(\mathop {\lim }\limits_{x \to 1} \dfrac{{4 – \sqrt[3]{{3{x^2} + 5}}}}{{x + 1}}\) bằng:
A. \( + \infty \) B. \( – 1\)
C. 1 D. \( – \infty \)
5. Cho hàm số \(f\left( x \right) = \left\{ \begin{array}{l}1 – 2x + 3{x^2},\,\,x \ne 2\\m – 4\,\,\,\,\,\,\,\,\,\,\,\,\,,\,x = 2\end{array} \right.\). Với giá trị nào của tham số \(\;m\) thì hàm số đã cho liên tục tại điểm \(x = 2\)?
A. 11 B. 9
C. 13 D. 11
6. Tính\(\mathop {\lim }\limits_{x \to {{\left( { – 3} \right)}^ – }} \dfrac{{x – 3}}{{x + 3}}\)
A. \( – \infty \) B. \( + \infty \)
C. 1 D. -3
7. Cho hàm số \(y = 3\sqrt {2 – {x^2}} \). Hàm số đã cho liên tục tại điểm
A. \(x = \sqrt 2 \) B. \(x = 3\)
C. \(x = – \sqrt 2 \) D. \(x = – 1\)
8. \(\lim \left( {3 – 2n + 4{n^3}} \right)\) bằng:
A. \( + \infty \) B. \( – \infty \)
C. 3 D. 4
9. Cho hàm số \(y = f(x)\). Biểu thức nào sau đây dùng để tính đạo hàm của hàm số trên tại \({{\rm{x}}_0} = 1\)
A. \(\mathop {\lim }\limits_{\Delta x \to 1} {\mkern 1mu} \dfrac{{f(1 + \Delta x) – f(1)}}{{\Delta x}}\)
B. \(\mathop {\lim }\limits_{\Delta x \to 1} {\mkern 1mu} \dfrac{{f(x) – f(1)}}{{x – 1}}\)
C. \(\mathop {\lim }\limits_{\Delta x \to 0} {\mkern 1mu} \dfrac{{f(1 + \Delta x) – f(1)}}{{\Delta x}}\)
D. \(\mathop {\lim }\limits_{\Delta x \to 0} {\mkern 1mu} \dfrac{{f(1 + \Delta x) – f(\Delta x)}}{{\Delta x}}\)
10: Biểu thức nào sau đây là đạo hàm của hàm số \(y = 2{x^4} – 3{x^3} + 4{x^2} – 1\)
A. \(y’ = 8{{\rm{x}}^3} – 9{x^2} + 8x\)
B. \(y’ = 8{{\rm{x}}^3} + 9{x^2} + 8x\)
C. \(y’ = 8{{\rm{x}}^3} – 9{x^2} – 8x\)
D. \(y’ = – 8{{\rm{x}}^3} – 9{x^2} + 8x\)
11: Xét hàm số \(y = {\sin ^2}2x\). Biểu thức nào sau đây là đúng
A. \(y + y’ = \left( {\sin 2x + 2\cos 2x} \right)\sin 2x\)
B. \(y – y’ = \left( {\sin 2x – 2\cos 2x} \right)\sin 2x\)
C. \(y – y’ = \left( {\sin 2x – \cos 2x} \right)\sin 2x\)
D. \(y + y’ = \left( {\sin 2x + 4\cos 2x} \right)\sin 2x\)
Advertisements (Quảng cáo)
12: Xét hàm số\(y = \dfrac{{x + 1}}{{2x – 1}}\). Giá trị \(y'(1)\) bằng :
A. \(2\) B. \( – 3\)
C. \(3\) D. \(0\)
13: Xét chuyển động của vật M xác định bởi phương trình \(s = f(t) = 3{t^2} + 2\sqrt {2t + 1} \)(m) trong đó t là thời gian.Vận tốc tức thời của M tại thời điểm \({t_0} = 4{\rm{s}}\)bằng
A. \(24\dfrac{1}{3}\left( {\dfrac{m}{s}} \right)\)
B. \(24\dfrac{2}{3}\left( {\dfrac{m}{s}} \right)\)
C. \(\dfrac{{76}}{3}\left( {\dfrac{m}{s}} \right)\)
D. \(24\left( {\dfrac{m}{s}} \right)\)
14: Xét hàm số \(y = {x^3} – 6{x^2} + 9x – 2\). Tập nghiệm của bất phương trình \(y’ \ge 0\) là
A. \(1 \le {\rm{x}} \le 3\)
B. \(R\backslash \left[ {1;3} \right]\)
C. \(\left( { – \infty ;1} \right] \cup \left[ {3; + \infty } \right)\)
D. \(\left[ \begin{array}{l}x \ge 3\\x \le 1\end{array} \right.\)
15: Xét hàm số \(y = x + \sqrt {8 – {x^2}} \). Phương trình \(y’ = 0\) có bao nhiêu nghiệm?
A. \(1\) B. \(2\)
C. \(0\) D. \(3\)
16: Xét hàm số \(y = {{\rm{x}}^2} + 3x + 2\) có đồ thị là (C). Tiếp tuyến của (C) tại điểm có hoành độ \({{\rm{x}}_0} = 0\) có phương trình là:
A. \(3{\rm{x}} + y – 2 = 0\) B. \(y = 3x + 3\)
C. \(y = – 3x – 2\) D. \(3x – y + 2 = 0\)
17: Viết phương trình tiếp tuyến với đồ thị hàm số \(y = 3{x^2} + 2x + 1\) biết tiếp tuyến song song với đường thẳng \(d:y = – 4x + 1\)
A. \(y = – 4x + 2\) B. \(y = – 4x – 3\)
C. \(y = – 4x – 2\) D. \(y = – 4x + 6\).
18: Cho hình hộp ABCD.A’B’C’D’ khi đó véc tơ \(\overrightarrow {AB} \) bằng véc tơ:
A. \(\overrightarrow {CC’} \)
B. \(\overrightarrow {C’D’} \)
C. \(\overrightarrow {D’C’} \)
D. \(\overrightarrow {A’D’} \)
Advertisements (Quảng cáo)
19: Cho hình hộp chữ nhật ABCD.A’B’C’D’ khi đó véc tơ \(\overrightarrow {AD’} \)cùng phương với véc tơ:
A. \(\overrightarrow {C’B} \)
B. \(\overrightarrow {A’A} \)
C. \(\overrightarrow {DC} \)
D. \(\overrightarrow {DA} \)
20: Cho hình lập phương cạnh\(\;a\). Khi đó góc của ( \(\overrightarrow {AB} \), \(\overrightarrow {CC’} \) ) bằng
A. \({45^0}\) B. \({0^0}\)
C. \({90^0}\) D. \({180^0}\)
21: Cho hình chóp \(S.{\rm{ }}ABCD\) có đáy \(ABCD\) là hình vuông và tất cả các cạnh đều bằng\(a\). Khi đó tích vô hướng của \(\overrightarrow {AS} \).\(\overrightarrow {A{\rm{D}}} \) là:
A. \(\dfrac{{{a^2}\sqrt 3 }}{2}\)
B. \({a^2}\)
C. \(0\)
D. \(\dfrac{{{a^2}}}{2}\)
22: Cho hình chop\(S.ABCD\). Cặp đường thẳng \(SC\) và đường thẳng nào sau đây chéo nhau:
A. \(AC\) B. \(SB\)
C. \(SA\) D. \(AB\)
23: Cho hình chóp \(S.{\rm{ }}ABCD\) có \(SH\) là đường cao . Khi đó góc của cạnh bên \(SA\) và mặt đáy là:
A. \(\widehat {SAH}\) B. \(\widehat {SBH}\)
C. \(\widehat {SCH}\) D. \(\widehat {SDH}\)
II. PHẦN TỰ LUẬN
1. (1,5đ): Tính các giới hạn sau:
a. \(\lim \dfrac{{4{n^2} – 12n + 9}}{{1 – n + 2{n^2}}}\)
b. \(\mathop {\lim }\limits_{x \to – 4} \dfrac{{3\sqrt {2 – x} – 2}}{{x – 4}}\)
c. \(\mathop {\lim }\limits_{x \to 2} \dfrac{{{x^2} + 5x – 14}}{{{x^2} + 3x – 10}}\)
2. (0,5đ): Tìm điều kiện của m để hàm số \(y = f\left( x \right) = \left\{ \begin{array}{l}\dfrac{{\sqrt {x + 3} – 2}}{{x – 1}}\,khi\,x > 1\\3x + m\,\,\,\,khi\,\,\,\,\,x \le 1\end{array} \right.\) liên tục tại điểm \(x = 1\)
3. (1đ): Tính đạo hàm của các hàm số sau
a. \(y = 2{x^3} + 3{x^2} – 4\)
b.\(y = {\cot ^4}\left( {\sqrt {3x – 1} } \right)\)
4. (1,5đ): Cho hình chóp \(S.ABC\) có đáy là tam giác \(ABC\) vuông tại \(B\) và có cạnh \(SA\) vuông góc với mặt phẳng \(\left( {ABC} \right).\)
a) Chứng minh các mặt hình chóp là các tam giác vuông
b) Gọi \(AH\) là đường cao tam giác\(SAB\). Chứng minh \(AH\) vuông góc mặt phẳng \(\left( {SBC} \right)\)
c) Biết \(SC\) tạo với mặt phẳng \(\left( {ABC} \right)\) một góc 450, \(SA = a\sqrt 3 \), \(BC = a\sqrt 2 \). Tính góc hai mặt phẳng \(\left( {SBC} \right)\) và \(\left( {ABC} \right)\)
5. (0,5đ): Xác định \(n\) nguyên dương thỏa mãn:
\(C_{2017}^0 + 2C_{2017}^1 + 3C_{2017}^2 + 4C_{2017}^3 + …\)\(\,+ 2018C_{2017}^{2017} = {2^{2016}}\left( {2n + 1} \right)\)

I. PHẦN TRẮC NGHIỆM:
|
1 |
2 |
3 |
4 |
5 |
|
B |
A |
A |
C |
C |
|
6 |
7 |
8 |
9 |
10 |
|
B |
D |
A |
C |
A |
|
11 |
12 |
13 |
14 |
15 |
|
D |
B |
B |
C |
A |
|
16 |
17 |
18 |
19 |
20 |
|
D |
C |
C | A |
C |
|
21 |
22 |
23 |
|
|
|
D |
D |
A |
|
II. PHẦN TỰ LUẬN
1.
\(a)\,\,\lim \dfrac{{4{n^2} – 12n + 9}}{{1 – n + 2{n^3}}} \)\(\,= \lim \dfrac{{4 – \dfrac{{12}}{n} + \dfrac{9}{{{n^2}}}}}{{\dfrac{1}{{{n^2}}} – \dfrac{1}{n} + 2}} = 2\)
\(b)\,\mathop {\lim }\limits_{x \to – 4} \dfrac{{3\sqrt {2 – x} – 2}}{{x – 4}} = \dfrac{{3\sqrt 6 – 2}}{{ – 8}}\)
\(c)\,\,\mathop {\lim }\limits_{x \to 2} \dfrac{{{x^2} + 5x – 14}}{{{x^2} + 3x – 10}}\)\(\, = \mathop {\lim }\limits_{x \to 2} \dfrac{{\left( {x – 2} \right)\left( {x + 7} \right)}}{{\left( {x – 2} \right)\left( {x + 5} \right)}} \)\(\,= \mathop {\lim }\limits_{x \to 2} \dfrac{{x + 7}}{{x + 5}} = \dfrac{9}{7}\)
2. TXĐ: \(D = R\) và \({x_0} = 1 \in D\)
+ \(f\left( 1 \right) = 3 + m\)
+ \(\mathop {\lim }\limits_{x \to {1^ + }} f\left( x \right) = \mathop {\lim }\limits_{x \to {1^ + }} \dfrac{{\sqrt {x + 3} – 2}}{{x – 1}}\)\(\, = \mathop {\lim }\limits_{x \to {1^ + }} \dfrac{{x – 1}}{{\left( {x – 1} \right)\left[ {\sqrt {x + 3} + 2} \right]}}\)
\( = \mathop {\lim }\limits_{x \to {1^ + }} \dfrac{1}{{\sqrt {x + 3} + 2}} = \dfrac{1}{4}\)
+ \(\mathop {\lim }\limits_{x \to {1^ + }} f\left( x \right) = \mathop {\lim }\limits_{x \to {1^ + }} \left( {3x + m} \right) = 3 + m\)
Để hàm số liên tục tại điểm \({x_0} = 1\) thì:
\(\mathop {\lim }\limits_{x \to {1^ + }} f\left( x \right) = \mathop {\lim }\limits_{x \to {1^ – }} f\left( x \right) = f\left( 1 \right)\)
\(\Leftrightarrow 3 + m = \dfrac{1}{4} \Leftrightarrow m = – \dfrac{{11}}{4}\)
3.
\(a)\,\,y’ = 6{x^2} + 6x\)
\(\begin{array}{l}b)\,\,y = {\cot ^4}\left( {\sqrt {3x – 1} } \right)\\y’ = 4{\cot ^3}\left( {\sqrt {3x – 1} } \right)\left( { – \dfrac{3}{{2\sqrt {3x – 1} .{{\sin }^2}\sqrt {3x – 1} }}} \right)\end{array}\)
4.
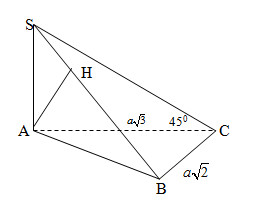
a) Tam giác \(ABC\) vuông theo giả thiết
\(SA \bot mp\left( {ABC} \right) \Rightarrow \Delta SAC\) vuông tại \(A,\Delta SAB\) vuông tại \(A\).
\(SA \bot mp\left( {ABC} \right) \Rightarrow SA \bot BC\) và \(AB \bot BC \Rightarrow BC \bot mp\left( {SAB} \right) \) \(\Rightarrow BC \bot SB\). Vậy tam giác \(SBC\) vuông tại \(B\)
b) Theo CM trên:\(BC \bot mp\left( {SAB} \right) \Rightarrow BC \bot AH\) , mà \(AH \bot SB \Rightarrow AH \bot mp\left( {SBC} \right)\)
c) Xác định góc \(mp\left( {SBC} \right)\) và \(mp\left( {ABC} \right)\) là \(\widehat {SBA}\)
Xác định góc \(SC\) và \(mp\left( {ABC} \right)\) là \(\widehat {SCA}\)\( = 45^\circ \) .
\( \Rightarrow SA = AC = \)\(a\sqrt 3 \)
Xét tam giác vuôg\(ABC\) : \({\rm{A}}{B^2} = A{C^2} – B{C^2} = {a^2}\), vậy \(AB = a\)
Vậy \(\tan \widehat {SBA}\)\( = \dfrac{{SA}}{{AB}} = \)\(\sqrt 3 \)Þ\(\widehat {SBA}\)\( = 60^\circ \).
5.Xét f(x)
\(\begin{array}{l}f(x) = x{\left( {1 + x} \right)^{2017}} \\= xC_{2017}^0 + {x^2}C_{2017}^1 + {x^3}C_{2017}^2 + {x^4}C_{2017}^3 + … + {x^{2018}}C_{2017}^{2017}\\f'(x) = {\left( {1 + x} \right)^{2017}} + x.2017{\left( {1 + x} \right)^{2016}}\\ = C_{2017}^0 + 2xC_{2017}^1 + 3{x^2}C_{2017}^2 + 4{x^3}C_{2017}^3 +… + 2018{x^{017}}C_{2017}^{2017}\\f'(1) = {2^{2017}} + {2017.2^{2016}} \\= C_{2017}^0 + 2C_{2017}^1 + 3C_{2017}^2 + 4C_{2017}^3 + … + 2018C_{2017}^{2017}\\ \Rightarrow {2019.2^{2016}} = {2^{2016}}\left( {2n + 1} \right)\\ \Rightarrow n = 1009\end{array}\)






