1.Tìm nguyên hàm của hàm số \(f(x) = {x^{\sqrt 5 }}.\)
A. \(\int {f(x)} dx = \dfrac{1}{{\sqrt 5 – 1}}{x^{\sqrt 5 – 1}} + C.\)
B. \(\int {f(x)} dx = {x^{\sqrt 5 + 1}} + C.\)
C. \(\int {f(x)dx} = \dfrac{1}{{\sqrt 5 + 1}}{x^{\sqrt 5 + 1}} + C.\)
D. \(\int {f(x)} dx = \sqrt 5 {x^{\sqrt 5 – 1}} + C.\)
2. Trong các khẳng định sau, khẳng định nào sai?
A. \(\int {0dx} = C.\)
B. \(\int {dx} = x + C.\)
C. \(\int {{x^e}dx} = \dfrac{{{x^{e + 1}}}}{{e + 1}} + C.\)
D. \(\int {{5^x}dx} = \dfrac{{{5^{x + 1}}}}{{x + 1}} + C.\)
3. Tính tích phân \(I = \int\limits_1^2 {\dfrac{1}{{{x^6}}}} dx.\)
A. \(I = – \dfrac{{31}}{{125}}.\)
B. \(I = \dfrac{{31}}{{125}}.\)
C. \(I = \dfrac{{31}}{{160}}.\)
D. \(I = \dfrac{{24}}{{125}}.\)
4. Cho hàm số f(x) liên tục trên đoạn \(\left[ { – 5;3} \right]\) và F(x) là một nguyên hàm của f(x), biết \(F( – 5) = 3,F(3) = \dfrac{{15}}{7}.\) Tính tích phân \(I = \int\limits_{ – 5}^3 {\left[ {7f(x) – x} \right]dx} .\)
A. I = 2. B. I = 11.
C. I = 19. D.\(I = \dfrac{7}{2}.\)
5. Tính tích phân \(\int\limits_0^1 {(4x + 3){e^x}} dx.\)
A. 3e + 1. B. 3e – 1.
C. – 3e – 1. D. 1 – 3e.
6. Một vật chuyển động với gia tốc \(a(t) = 6{t^2} + 2t(m/{s^2}).\) Vận tốc ban đầu của vật là 2 (m/s). Hỏi vận tốc của vật là bao nhiêu sau khi chuyển động với gia tốc đó đượ 2s.
A. 29 m/s. B. 22 m/s.
C. 18 m/s. D. 20 m/s.
7. Cho \(\int\limits_0^1 {f(x)dx = 16.} \) Tính \(I = \int\limits_0^{\dfrac{\pi }{4}} {f(\sin 2x).cos2xdx.} \)
A. I = 5. B. I = 9.
C. I = 8. D. I = 10.
8. Hình phẳng giới hạn bởi các đường x = -3, x = 1, \(y = {x^2} – x\) có diện tích được tính theo công thức:
A.\(S = \int\limits_{ – 3}^1 {({x^2}} – x)dx\,\,\,\,\,\,\,\)(đvdt).
B.\(S = \int\limits_{ – 3}^0 {({x^2}} – x)dx – \int\limits_0^1 {({x^2}} \, – x)dx\,\,\,\,\,\,\)(đvdt).
C.\(S = \int\limits_{ – 3}^0 {({x^2}} – x)dx\, + \int\limits_0^1 {({x^2}} \, – x)dx\,\,\,\,\,\)(đvdt).
D.\(S = \int\limits_0^1 {\left| {{x^2} – x} \right|} dx\,\,\,\,\,\,\,\)(đvdt).
9. Cho hình phẳng (H) giới hạn bởi các đường \(y = {x^3}\) và \(y = \sqrt x .\) Khối tròn xoay tạo ra khi (H) quay quanh Ox có thể tích là:
A.\(\pi \int\limits_0^1 {({x^6}} – x)dx\) (đvtt).
B.\(\pi \int\limits_0^1 {({x^3}} – \sqrt x )dx\) (đvtt).
C.\(\pi \int\limits_0^1 {(\sqrt x } – {x^3})dx\) (đvtt).
D.\(\pi \int\limits_0^1 {(x – {x^6}} )dx\) (đvtt).
10: Biết \(\int\limits_2^4 {\dfrac{{{x^2} + 2x + 2}}{{x + 2}}} dx = a + 2\ln \dfrac{b}{2}\) với a, b là các số nguyên. Tính S = a – 2b.
A. S = 2. B. S = 10.
C. S = 5. D. S = 0.
11: Một bác thợ xây bơm nước vào bể chứa nước. Gọi h(t) là thể tích nước bơm được sau t giây. Cho \(h'(t) = 6a{t^2} + 2bt\) và ban đầu bể không có nước. Sau 3 giây thì thể tích nước trong bể là \(90{m^3},\) sau 6 giây thì thể tích nước trong bể là \(504{m^3}.\) Tính thể tích nước trong bể sau khi bơm được 9 giây.
A. \(1458{m^3}.\) B.\(600{m^3}.\)
C.\(2200{m^3}.\) D.\(4200{m^3}.\)
12: Cho (H) là hình phẳng giới hạn bởi đường cong \((C):y = – {x^2} + 4x\) và đường thẳng D: y = x. Tính thể tích V của vật thể tròn xoay do hình phẳng (H) quay quanh trục hoành.
A.\(V = \dfrac{{81\pi }}{{10}}.\)
B.\(V = \dfrac{{81\pi }}{5}.\)
C.\(V = \dfrac{{108\pi }}{5}.\)
D.\(V = \dfrac{{108\pi }}{{10}}.\)
13: Tính diện tích hình phẳng giơi hạn bởi hai đồ thị \(({C_1}):y = {x^2} + 2x\) và \(({C_2}):y = {x^3}.\)
A. \(S = \dfrac{{83}}{{12}}.\) B. \(S = \dfrac{{15}}{4}.\)
C. \(S = \dfrac{{37}}{{12}}.\) D. \(S = \dfrac{9}{4}.\)
14: Thể tích khối vật thể tròn xoay khi quay hình phẳng (S) giới hạn bởi các đường \(y = 4 – {x^2},y = 0\) quanh trục hoành có kết quả dạng \(\dfrac{{\pi a}}{b}\) và \(\dfrac{a}{b}\) là phân số tối giản. Khi đó a – 30b bằng:
A. 62. B. 26.
C. 82. D. 28.
15: Trong mặt phẳng tọa độ Oxy, cho hình thang ABCD với A(-2;3), B(3;6), C(3;0),D(9-2;0). Quay hình thang ABCD xung quanh trục Ox thì thể tích khối tròn xoay tạo thành bằng bao nhiêu?
A. \(72\pi .\) B. \(74\pi .\)
C. \(76\pi .\) D. \(105\pi .\)
16: Cho số phức z thỏa mãn (1+2i)z = 6 – 3i. Tìm phần thực của z.
A. 3. B. – 3i.
C. 0. D.\(\dfrac{9}{5}.\)
Advertisements (Quảng cáo)
17: Cho hai số phức z = 6 + 5i, \(z’ = 5 – 4i + z.\) Tìm môđun của số phức \({\rm{w}} = z.z’.\)
A. \(\left| {\rm{w}} \right| = 612.\) B. \(\left| {\rm{w}} \right| = 61.\)
C. \(\left| {\rm{w}} \right| = 61\sqrt 2 .\) D. \(\left| {\rm{w}} \right| = 6\sqrt 2 .\)
18: Tìm tất cả các giá trị thực của tham số m để số phức \(z = \dfrac{{m + 2i}}{{m – 2i}}\) có phần thực dương
A. m > 2. B.\(\left[ \begin{array}{l}m < – 2\\m > 2\end{array} \right..\)
C. -2 < m < 2. D.m < – 2.
19: Cho số phức z có \(\left| z \right| = 9.\) Tập hợp các điểm M tring mặt phẳng tọa độ Oxy biểu diễn số phức \({\rm{w}} = \overline z + 5i\)là một đường tròn. Tính bán kính đường tròn đó.
A. 9. B.\(\dfrac{9}{5}.\)
C. 3. D. \(9\sqrt 2 .\)
20: Gọi \({z_1}\) và \({z_2}\) là hai nghiệm của phương trình \({z^2} – 2z + 7 = 0\) biết \(({z_1} – {z_2})\) có phần ảo là số thực âm. Tìm phần thực của số phức \({\rm{w}} = 2z_1^2 – z_2^2.\)
A.\(6\sqrt 6 .\) B.\( – 6\sqrt 6 .\)
C. 5. D. – 5.
21: Tìm điểm M biểu diễn số phức z = i – 2.
A. M = (1;-2). B. M (2;1).
C. M(2;-1). D. M = (-2;1).
22: Ký hiệu \({z_1},{z_2}\) là các nghiệm phức của phương trình \({z^2} – 6z + 10 = 0\,\,({z_1}\) có phần ảo âm). Tìm số phức liên hợp của số phức \({\rm{w}} = 3z_1^2 – 2z_2^2 + 1.\)
A.\(\overline {\rm{w}} = 9 + 30i.\)
B. \(\overline {\rm{w}} = 9 – 30i.\)
C. \(\overline {\rm{w}} = 9 – 10i.\)
D. \(\overline {\rm{w}} = 30 – 9i.\)
23: Tìm môđun của số phức \({\rm{w}} = (1 + z)\overline z \) biết rằng số phức z thỏa mãn biểu thức \((3 + 2i)z + {(2 – i)^2} = 4 + i.\)
A. \(\left| {\rm{w}} \right| = 2.\) B. \(\left| {\rm{w}} \right| = \sqrt {10} .\)
C. \(\left| {\rm{w}} \right| = \sqrt 8 .\) D. \(\left| {\rm{w}} \right| = \sqrt 2 .\)
24: Tìm số phức z thỏa mãn (2 + 3i)(z – 2) + 13 – 13i = 0.
A. z = 3 – 5i. B. z = 5 + 3i.
C. z = 3 + 5i. D. z = 5 – 3i.
25: Cho \(z = \dfrac{{3 + i}}{{x + i}}.\) Tổng phần thực và phần ảo của z là:
A. \(\dfrac{{2x – 4}}{2}.\)
B. \(\dfrac{{4x + 2}}{2}.\)
C. \(\dfrac{{4x – 2}}{{{x^2} + 1}}.\)
D. \(\dfrac{{2x + 6}}{{{x^2} + 1}}.\)
26: Cho số phức z có số phức liên hợp là \(\overline z .\) Gọi M và \(M’\) tương ứng, lần lượt là điểm biểu diễn hình học của z và \(\overline z .\) Hãy chọ mệnh đề đúng.
A. M và \(M’\) đối xứng qua trục thực.
B. M và \(M’\) trùng nhau.
C. M và \(M’\) đối xứng qua gốc tọa độ.
D. M và \(M’\) đối xứng qua trục ảo.
27: Kí hiệu \({z_1};{z_2};{z_3};{z_4}\) là 4 nghiệm của số phức \({z^4} – 5{z^2} – 36 = 0.\) Tính tổng \(T = \left| {{z_1}} \right| + \left| {{z_2}} \right| + \left| {{z_3}} \right| + \left| {{z_4}} \right|.\)
A. T = 6. B. T = -4.
C. T = 10. D.\(T = 6 + 2\sqrt 3 .\)
Advertisements (Quảng cáo)
28: Tìm số phức z thỏa mãn \(zi + 2\overline z = 4 – 4i.\)
A. z = 4 – 4i. B. z = 3 – 4i.
C. z = 3 + 4i. D. z = 4 + 4i.
29: Cho phương trình \({z^2} + bz + c = 0.\) Xác định b và c nếu phương trình nhận z = 1 – 3i làm một nghiệm?
A. b = – 2, c = 10. B. b = 6, c = 10.
C. b = -6, c = -10. D. b = -6, c = 10.
30: Trong mặt phẳng tọa độ, hãy tính số phức z có môđun nhỏ nhất, biết rằng số phức z thỏa mãn điều kiện \(\left| {z – 2 – 4i} \right| = \sqrt 5 .\)
A. z = – 1 – 2i. B. z = 1 – 2i.
C. z = – 1 + 2i. D. z = 1 + 2i.
31: Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S): \({(x – 9)^2} + {(y – 1)^2} + {(z – 1)^2} = 25.\) Tìm tâm I và tính bán kính R của (S).
A. I (9;1;1) và R = 5.
B. I(9;-1;-1) và R = 5.
C. I(9;1;1) và R = 25.
D. I(9;1;-1) và R = 25.
32: Trong không gian với hệ tọa độ Oxyz, cho điểm A(2;2;1) và mặt phẳng (P): x + 2y – 2z – 1 = 0. Viết phương trình mặt cầu tâm A và tiếp xúc với mặt phẳng (P).
A. \({(x – 2)^2} + {(y + 2)^2} + {(z + 1)^2} = 3.\)
B. \({(x – 2)^2} + {(y – 2)^2} + {(z – 1)^2} = 1.\)
C. \({(x + 2)^2} + {(y – 2)^2} + {(z – 1)^2} = 1.\)
D. \({(x – 2)^2} + {(y + 2)^2} + {(z – 1)^2} = 1.\)
33: Trong không gian với hệ tọa độ Oxyz, cho hai điểm A(1;2;3) và B(-1;4;1). Phương trình mặt cầu đường kính AB là:
A. \({x^2} + {(y – 3)^2} + {(z – 2)^2} = 3.\)
B. \({(x – 1)^2} + {(y – 2)^2} + {(z – 3)^2} = 12.\)
C. \({(x + 1)^2} + {(y – 4)^2} + {(z – 1)^2} = 12.\)
D. \({x^2} + {(y – 3)^2} + {(z – 2)^2} = 12.\)
34: Trong không gian với hệ tọa độ Oxyz cho mặt cầu S(I;R) có tâm I = (1;1;3) và bán kính \(R = \sqrt {10} .\) Hỏi có bao nhiêu giao điểm giữa mặt cầu S với các trục tọa độ Ox, Oy và Oz.
A. 1. B. 2.
C. 4. D. 6.
35: Trong không gian với hệ tọa độ Oxyz, tìm m để phương trình \({x^2} + {y^2} + {z^2} – 2mx – 2(m + 2)y \)\(\,- 2(m + 3)z + 16m + 13 = 0\) là phương trình của một mặt cầu.
A.m < 0 hay m > 2.
B.\(m \le 2\) hay \(m \ge 0.\)
C. m < -2 hay m > 0.
D.\(m \le 0\) hay \(m \ge 2.\)
36: Trong hệ tọa độ Oxyz, xác định phương trình của mặt cầu (S) đi qua A(-1;2;0), B( -2; 1;1) và có tâm nằm trên trục Oz.
A. \({x^2} + {y^2} + {z^2} – z – 5 = 0.\)
B. \({x^2} + {y^2} + {z^2} + 5 = 0.\)
C. \({x^2} + {y^2} + {z^2} – x – 5 = 0.\)
D. \({x^2} + {y^2} + {z^2} – y – 5 = 0.\)
37: Trong không gian vơi hệ trục tọa độ Oxyz, cho mặt phẳng \((\alpha ):y – 2z + 4 = 0.\) Vec tơ nào dưới đây là vec tơ pháp tuyến của \((\alpha )?\)
A. \(\overrightarrow {{n_2}} = (1; – 2;0).\)
B. \(\overrightarrow {{n_1}} = (0;1; – 2).\)
C. \(\overrightarrow {{n_3}} = (1;0; – 2).\)
D. \(\overrightarrow {{n_4}} = (1; – 2;4).\)
38: Trong không gian với hệ trục tọa độ Oxyz, cho điểm A(2;1;-1), B(1;0;1) và mặt phẳng (P): x + 2y – z + 1 = 0. Viết phương trình mặt phẳng (Q) qau A, B và vuông góc với (P).
A. (Q): 2x – y + 3 = 0.
B. (Q): 3x – y + z – 4 = 0.
C. (Q): – x + y + z = 0.
D. (Q): 3x – y + z = 0.
39: Trong không gian với hệ tọa độ Oxyz, cho ba điểm A(3;0;-1), B(1;-1;3), C(0;1;3). Viết phương trình mặt phẳng đi qua ba điểm A, B, C.
A. 8x + 4y + 5z – 19 = 0.
B. 10x + 3y + z – 19 = 0.
C. 2x – y + z – 3 = 0.
D. 10x – 3y – z – 21 = 0.
40: Trong không gian với hệ tọa độ Oxyz, mặt phẳng (P) cắt ba trục Ox, Oy, Oz tại A, B, C; trực tâm tam giác ABC là H(4;5;6). Phương trình của mặt phẳng (P) là:
A. 4x + 5y + 6z – 77 = 0.
B. 4x + 5y + 6z + 14 = 0.
C.\(\dfrac{x}{4} + \dfrac{y}{5} + \dfrac{z}{6} = 1.\)
D.\(\dfrac{x}{4} + \dfrac{y}{5} + \dfrac{z}{6} = 0.\)
41: Trong không gian với hệ tọa độ Oxyz, cho A(2;3;4), B(4;6;2), C(3;0;6). Gọi G là trọng tâm tam giác ABC. Biết điểm M nằm trên mặt phẳng (Oxy) sao cho đoạn thẳng GM ngắn nhất. Tính độ dài đoạn thẳng GM.
A. GM = 4. B.\(GM = \sqrt 5 .\)
C. GM = 3. D.\(GM = 5\sqrt 2 .\)
42: Trong không gian với hệ tọa độ Oxyz, cho điểm A(1;1;1) và đường thẳng (d): \(\left\{ \begin{array}{l}x = 4 – t\\y = 1 – t\\z = 1 + t\end{array} \right..\) Tìm tọa độ hình chiếu \(A’\) của A trên (d).
A.\(A'(2;3;0).\) B.\(A'( – 2;3;0).\)
C.\(A'(3;0;2).\) D.\(A'( – 3;0; – 2).\)
43: Trong không gian Oxyz, cho hai mặt phẳng (P): 3x – my – z + 7 = 0, (Q): 6x + 5y – 2z – 4 = 0. Xác định m để hai mặt phẳng (P) và (Q) song song với nhau.
A. m = 4. B.\(m = – \dfrac{5}{2}.\)
C. m = -30. D.\(m = \dfrac{5}{2}.\)
44: Trong không gian với hẹ tọa độ Oxyz, cho hai đường thẳng d: \(\left\{ \begin{array}{l}x = 1 + t\\y = t\\z = – 1 + 2t\end{array} \right.,(t \in \mathbb{R}),\) \(d’\left\{ \begin{array}{l}x = 1 – t’\\y = 2 + 2t’\\z = 3 – t’\end{array} \right.,(t’ \in \mathbb{R}).\) Giá trị của tham số m để hai đường thẳng d và \(d’\)cắt nhau là:
A. m = -1. B. m = 1.
C. m = 0. D. m = 2.
45: Trong không gian với hệ tọa độ Oxyz, cho điểm M(2;3;4) và mặt phẳng (P): 2x + 3y – 7z + 1 = 0. Viết phương trình đường thằng d đi qua M và vuông góc (P).
A. \(d:\dfrac{{x – 2}}{2} = \dfrac{{y – 3}}{3} = \dfrac{{z + 7}}{4}.\)
B. \(d:\dfrac{{x – 2}}{2} = \dfrac{{y – 3}}{3} = \dfrac{{z – 4}}{{ – 7}}.\)
C. \(d:\dfrac{{x + 2}}{2} = \dfrac{{y + 3}}{3} = \dfrac{{z – 7}}{4}.\)
D. \(d:\dfrac{{x + 2}}{2} = \dfrac{{y + 3}}{3} = \dfrac{{z + 4}}{{ – 7}}.\)
46: Trong không gian với hệ tọa độ Oxyz, cho hai đường thẳng \(d:\dfrac{{x – 1}}{3} = \dfrac{{y – 2}}{4} = \dfrac{{z – 3}}{5}\) và \(d’:\dfrac{{x – 4}}{6} = \dfrac{{y – 6}}{8} = \dfrac{{z – 8}}{{10}}.\) Mệnh đề nào dưới đây là đúng?
A.d vuông góc với \(d’.\)
B. d song song với \(d’.\)
C. d trùng với \(d’.\)
D. d và \(d’\)chéo nhau.
47: Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P): x + y – z – 1 = 0 và đường thẳng \(d:\dfrac{{x – 1}}{2} = \dfrac{{y – 2}}{1} = \dfrac{{z – 3}}{2}.\) Tìm giao điểm M của (P) và d.
A. M(3;-3;-5). B. M(3;3;-5).
C. M(3;3;5). D. M(-3;-3;-5).
48: Trong không gian Oxyz, cho A(1;3;-2), B(3;5;-12). Đường thẳng AB cắt mặt phẳng Oyz tại N. Tính tỉ số \(\dfrac{{BN}}{{AN}}.\)
A.\(\dfrac{{BN}}{{AN}} = 4.\)
B.\(\dfrac{{BN}}{{AN}} = 2.\)
C.\(\dfrac{{BN}}{{AN}} = 5.\)
D.\(\dfrac{{BN}}{{AN}} = 3.\)
49: Trong không gian với hệ tọa độ Oxyz, viết phương trình hình chiếu vuông góc của đường thẳng \(d:\dfrac{{x + 1}}{2} = \dfrac{{y – 2}}{3} = \dfrac{{z + 3}}{1}\) trên mặt phẳng tọa độ Oxy.
A. \(\left\{ \begin{array}{l}x = 3 – 6t\\y = 11 – 9t\\z = 0\end{array} \right..\)
B. \(\left\{ \begin{array}{l}x = 5 + 6t\\y = 11 – 9t\\z = 0\end{array} \right..\)
C. \(\left\{ \begin{array}{l}x = 5 – 6t\\y = 11 + 9t\\z = 0\end{array} \right..\)
D. \(\left\{ \begin{array}{l}x = 5 – 6t\\y = 11 – 9t\\z = 0\end{array} \right..\)
50: Một người có mảnh đất hình tròn có bán kính 5m, người này tính trồng cây trên mảnh đất đó, biết mỗi mét vuông trồng cây thu hoạch được 100 nghìn. Tuy nhiên cần có khoảng trống để dựng chòi và đồ dùng nên người này căng sợi dây 6m vào hai đầu mút dây mằm trên đường tròn xung quanh mảnh đất. Hỏi người này thu hoạch được bao nhiêu tiền (Tính theo đơn vị nghìn và bỏ số thập phân)
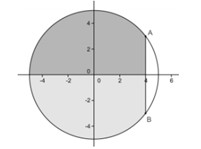
A. 3722. B. 7445.
C. 7446. D. 3723.

|
1 |
2 |
3 |
4 |
5 |
|
C |
D |
C |
A |
A |
|
6 |
7 |
8 |
9 |
10 |
|
B |
C |
B |
D |
D |
|
11 |
12 |
13 |
14 |
15 |
|
A |
C |
C |
A |
D |
|
16 |
17 |
18 |
19 |
20 |
|
C |
C |
B |
A |
D |
|
21 |
22 |
23 |
24 |
25 |
|
D |
A |
B |
C |
C |
|
26 |
27 |
28 |
29 |
30 |
|
A |
C |
D |
A |
D |
|
31 |
32 |
33 |
34 |
35 |
|
A |
B |
A |
C |
A |
|
36 |
37 |
38 |
39 |
40 |
|
A |
B |
B |
A |
A |
|
41 |
42 |
43 |
44 |
45 |
|
A |
C |
B |
C |
B |
|
46 |
47 |
48 |
49 |
50 |
|
C |
C |
D |
D |
B |





