I.PHẦN TRẮC NGHIỆM (7đ)
1. Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, \(SA \bot \left( {ABCD} \right)\). Trong các tam giác sau tam giác nào không phải là tam giác vuông?
A. \(\Delta {\rm{SBC}}\) B. \(\Delta {\rm{SAB}}\)
C. \(\Delta {\rm{SCD}}\) D. \(\Delta {\rm{SBD}}\)
2. Dãy số nào sau đây có giới hạn bằng 0?
A. \(\dfrac{{\sqrt {2{n^2} – 1} }}{{5n + 3{n^2}}}\)
B. \(\dfrac{{1 – 2{n^2}}}{{5n + 3{n^2}}}\)
C. \({u_n} = \dfrac{{{n^2} – 2n}}{{5n + 3}}\)
D. \({u_n} = \dfrac{{{n^2} – 2}}{{\sqrt {1 + 3{n^2}} }}\)
3. Khẳng định nào sau đây là đúng?
A. Hàm số \(f(x) = \dfrac{{x – 1}}{{x + 1}}\) gián đoạn tại \(x = 1\)
B. Hàm số \(f(x) = \dfrac{{x + 1}}{{{x^2} + 1}}\)liên tục trên \(R\)
C. Hàm số \(f(x) = \dfrac{{{x^2} – 1}}{{x + 1}}\) liên tục trên\(R\)
D. Hàm số \(f(x) = \dfrac{{x + 1}}{{x – 1}}\) liên tục trên \((0;2)\)
4. Giới hạn\(\mathop {\lim }\limits_{x \to {1^ – }} \dfrac{{2x + 3}}{{1 – x}}\) là:
A. \( – \infty \) B. \(2\)
C. \( + \infty \) D. \( – 2\)
5. Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm O và SA = SC. Khẳng định nào sau đây đúng ?
A. \(SO \bot (ABCD)\)
B. \(BD \bot (SAC)\)
C. \(AC \bot (SBD)\)
D. \(AB \bot (SAD)\)
6. Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, cạnh bên SA vuông góc với đáy. Khẳng định nào sau đây đúng ?
A. \((SCD) \bot (SAD)\)
B. \((SBC) \bot (SAC)\)
C. \((SDC) \bot (SAC)\)
D. \((SBD) \bot (SAC)\)
7. Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A, \((SAB) \bot (ABC)\), SA = SB , I là trung điểm AB. Khẳng định nào sau đây sai ?
A. Góc giữa \(SC\)và \((ABC)\)là \(\widehat {SCI}\)
B. \(SI \bot (ABC)\)
C. \(AC \bot (SAB)\)
D. \(AB \bot (SAC)\)
8. Một chất điểm chuyểnđộng có phương trình\(s = {t^3} + 3t\)(t tính bằng giây, s tính bằng mét) Tính vận tốc của chất điểm tại thời điểm \({t_0} = 2\) (giây) ?
A. \(15m/s\) B. \(7m/s\)
C. \(14m/s\) D. \(12m/s\)
9. Cho một hàm số f(x). Khẳng định nào sau đây là đúng?
A. Nếu \(f(a)f(b) < 0\) thì phương trình f(x)=0 có ít nhất một nghiệm trong khoảng \((a,b)\).
B. Nếu hàm số f(x) liên tục, đồng biến trên đoạn [a; b] và f(a).(b)>0 thì phương trình f(x)=0 không có nghiệm trong khoảng (a; b).
C. Nếu f(x) liên tục trên đoạn \(\left[ {a;b} \right],f(a).f(b) < 0\) thì phương trình f(x)=0 không có nghiệm trên khoảng \((a;b)\).
D. Nếu phương trình f(x)=0 có nghiệm trong khoảng (a; b) thì hàm số f(x) phải liên tục trên khoảng \((a;b)\)
10: \(\lim \left( {\sqrt {{n^2} + 3n} – \sqrt {{n^2} + 2} } \right) = \dfrac{a}{b}\) (\(a,b \in Z\) và \(\dfrac{a}{b}\) tối giản) thì tổng \({a^2} + {b^2}\) là :
Advertisements (Quảng cáo)
A. 10 B. 3
C. 13 D. 20
11: Cho hình chóp S.ABC có \(SA \bot \left( {ABC} \right)\) và H là hình chiếu vuông góc của S lên BC. Khẳng định nào sau đây đúng?
A. \(AC \bot SH\) B. \(BC \bot SC\)
C. \(AB \bot SH\) D. \(BC \bot AH\)
12: Hàm số\(y = \dfrac{{x + 6}}{{x + 9}}\) có đạo hàm là:
A. \(\dfrac{3}{{{{\left( {x + 9} \right)}^2}}}\)
B. \( – \dfrac{3}{{{{\left( {x + 9} \right)}^2}}}\)
C. \(\dfrac{{15}}{{{{\left( {x + 9} \right)}^2}}}\)
D. \( – \dfrac{{15}}{{{{\left( {x + 9} \right)}^2}}}\)
13: Cho hàm số \(f(x) = \dfrac{{a{x^2} + 4x + 3}}{{3x – 2a{x^2}}},(a \in R,a \ne 0)\). Khi đó \(\mathop {\lim }\limits_{x \to – \infty } f(x)\) bằng:
A. \(\dfrac{a}{3}\) B. \( – \dfrac{1}{2}\)
C. \( + \infty \) D. \( – \infty \)
14: . Hàm số\(y = {x^3} + 2{x^2} + \dfrac{{x + 4}}{2}\) có đạo hàm là:
A.\(y’ = 3{x^2} + 4x + \dfrac{1}{4}\)
B. \(y’ = 3{x^2} + 4x + 4\).
C.\(y’ = 3{x^2} + 4x + \dfrac{1}{2}\)
D. \(y’ = 3{x^2} + 4x + 2\)
15: Cho hàm số \(y = \sqrt {3x – 2} \). Phương trình tiếp tuyến của đồ thị hàm số biết tiếp tuyến song song với đường thẳng \(y = \dfrac{3}{2}x + \dfrac{1}{2}\) là:
A. \(y = \dfrac{3}{2}x – \dfrac{1}{2}\)
B. \(y = \dfrac{3}{2}x – 1\)
C. \(y = \dfrac{3}{2}x + 1\)
D. \(y = \dfrac{3}{2}x – \dfrac{3}{2}\)
16: Trong các dãy số sau, dãy số nào có giới hạn hữu hạn?
A. \({u_n} = \dfrac{{{n^3} – 2n + 3}}{{\sqrt {{n^4} + 4} }}\)
B. \({u_n} = \sqrt {{n^2} + 2n} – n\)
C. \({u_n} = \dfrac{{3{n^4} – 1}}{{\sqrt {{n^6} + 2} }}\)
Advertisements (Quảng cáo)
D. \({u_n} = \dfrac{{2{n^3} – n}}{{{n^2} – 2}}\)
17: Giới hạn \(\mathop {\lim }\limits_{x \to 0} \dfrac{{2 + \dfrac{3}{x}}}{{4 – \dfrac{1}{x}}}\) là:
A. \(\dfrac{1}{2}\) B. \(3\)
C. \(\dfrac{3}{4}\) D. \( – 3\)
18: Phương trình \({\mathop{\rm s}\nolimits} {\rm{inx}} = \mathop {\lim }\limits_{t \to 1} \dfrac{{2\sqrt {t + 3} – 4}}{{t – 1}}\), có nghiệm \(x \in (0;\dfrac{\pi }{2})\) là
A. \(\dfrac{\pi }{6}\) B. vô nghiệm
C. \({30^0}\) D. \(\dfrac{1}{2}\)
19: Biết \(\mathop {\lim }\limits_{x \to + \infty } \dfrac{{2x}}{{a + x}} = 2\), khi đó \(a\) có giá trị là:
A. \(1\)
B. Không tồn tại
C. \(\forall a \in R\)
D. \(0\)
20: Cho hàm số y = f(x) xác định trên tập số thực R thỏa mãn \(\mathop {\lim }\limits_{x \to 2} \dfrac{{f(x) – f(2)}}{{x – 2}} = 3\). Kết quả nào sau đây là đúng?
A. \(f’\left( 3 \right) = 2\) B. \(f’\left( 2 \right) = 3\)
C. \(f’\left( x \right) = 3\) D. \(f’\left( x \right) = 2\)
21: Đạo hàm của hàm số \(y = \sqrt {\sin 3x} \) là :
A. \(\dfrac{{3\cos 3x}}{{2\sqrt {\sin 3x} }}.\)
B. \(\dfrac{{\cos 3x}}{{2\sqrt {\sin 3x} }}.\)
C. \(\dfrac{{ – \cos 3x}}{{2\sqrt {\sin 3x} }}.\)
D. \(\dfrac{{ – 3\cos 3x}}{{2\sqrt {\sin 3x} }}.\)
22: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, có cạnh SA =\(a\sqrt 2 \) và SA vuông góc với mp(ABCD). Tính góc giữa đường thẳng SC và mp(ABCD) là:
A. \({\rm{4}}{{\rm{5}}^0}\)\(\) B. \({\rm{3}}{0^0}\)
C. \({\rm{6}}{0^0}\) D. \({\rm{9}}{0^0}\)
23: Cho hình chóp tứ giác đều S.ABCD có đáy tâm O và M, N lần lượt là trung điểm của BC, CD. Khẳng định nào sau đây là sai ?
A. \((SBD) \bot (SAC)\)
B. Góc giữa \((SBC)\)và \((ABCD)\)là \(\widehat {SMO}\)
C. Góc giữa \((SCD)\)và \((ABCD)\)là \(\widehat {NSO}\)
D. \((SMO) \bot (SNO)\)
24:Cho hàm số \(y = f(x) = {\cos ^2}x + m\sin x\) có đồ thị (C). Giá trị m để tiếp tuyến của (C) tại điểm có hoành độ \(x = \pi \) vuông góc với đường thẳng \(y = – x\) là:
A. Không tồn tại. B. \(0\).
C. \(1\). D. \( – 1\).
25: Hàm số \(y = \cos x – \sin x + 2x\) có đạo hàm là:
A. \( – \sin x + \cos x + 2\)
B. \(\sin x – \cos x + 2\).
C. \( – \sin x – \cos x + 2\).
D. \( – \sin x – \cos x + 2x\).
II.PHẦN TỰ LUẬN (3đ)
1. (1đ). Cho hàm số \(y = – \dfrac{1}{3}{x^3} + 2m{x^2} – 3mx + 2\sqrt 2 \) , m là tham số.
a)Giải bất phương trình \(y’ > 0\) khi \(m = 1\).
b)Tìm điều kiện của tham số\(m\) để \(y’ \le 0,\forall x \in R\) .
2.(0,75đ). Viết phương trình tiếp tuyến của đồ thị hàm số \(y = {x^3} + x\) tại điểm có hoành độ là 1.
3.(1,25 điểm ). Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm O, cạnh \(a\). Biết SA = SC, SB = SD, SO =\(\dfrac{{3a}}{4}\) và \(\widehat {ABC} = {60^0}\). Gọi I, J lần lượt là trung điểm của AB và BC.
a)Chứng minh \(SO \bot \left( {ABCD} \right),\,\,(SAC) \bot \left( {SBD} \right)\).
b). Tính khoảng cách giữa hai đường thẳng SO và IJ.
c) Tính góc giữa (SIJ) và mặt phẳng (SAC).

|
1D |
2A |
3B |
4C |
5C |
|
6A |
7D |
8A |
9B |
10C |
|
11D |
12A |
13B |
14C |
15A |
|
16B |
17D |
18A |
19C |
20B |
|
21A |
22A |
23C |
24D |
25C |
1.
a) \(y’ = – {x^2} + 4mx – 3m\). Khi m=1, \(y’ = – {x^2} + 4x – 3\)
\(y’ > 0\)\( \Leftrightarrow 1 < x < 3\). Vậy bất phương trình \(y’ > 0\) có nghiệm\(1 < x < 3\)
b) \(y’ \le 0,\forall x \in R\)\( \Leftrightarrow \Delta ‘ \le 0\)
\( \Leftrightarrow 4{m^2} – 3m \le 0 \Leftrightarrow 0 \le m \le \dfrac{3}{4}\)
2. \(y'(1) = 4\) , \(y(1) = 2\)
Phương trình tiếp tuyến cần tìm: \(y = y'(1)(x – 1) + y(1)\)
\( \Leftrightarrow y = 4(x – 1) + 2 = 4x – 2\)
3.
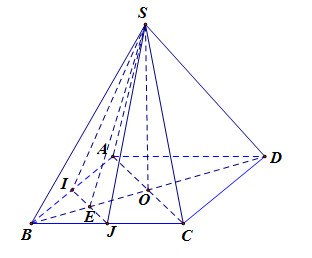
a)Chứng minh \(SO \bot \left( {ABCD} \right),\,\,(SAC) \bot \left( {SBD} \right)\).
\(\Delta \) SAC cân tại S nên\(SO \bot AC\), \(\Delta \)SBD cân tại S nên\(SO \bot BD\).Vậy \(SO \bot \left( {ABCD} \right).\)
\(\left\{ \begin{array}{l}AC \bot SO({\rm{Cm t}})\\AC \bot BD({\rm{ABCD \text{là hình thoi}}})\end{array} \right.\) \( \Rightarrow AC \bot (SBD) \Rightarrow (SAC) \bot (SBD)\)
b) \(E = BO \cap {\rm{IJ}}\)\( \Rightarrow \) E là trung điểm của BO. Do \(OE \bot {\rm{IJ;}}OE \bot {\rm{SO}}\)\( \Rightarrow \)\(d(SO,IJ) = {\rm{ }}OE\)
Tam giác ABC đều cạnh a nên \(BO = \dfrac{{a.\sqrt 3 }}{2}\).Vậy\(d(SO,IJ) = {\rm{ }}OE = \dfrac{{BO}}{2} = \dfrac{{a.\sqrt 3 }}{4}\)
c) Tính góc giữa (SIJ) và mặt phẳng (SAC).
Nhận thấy giao tuyến của (SIJ) và (SAC) song song với AC.
Theo trên\(AC \bot (SBD)\), do đó góc giữa (SIJ) và mặt phẳng (SAC) là\(\widehat {{\rm{OS}}E}\)
\(\tan \widehat {{\rm{OS}}E} = \dfrac{{OE}}{{SO}} = \dfrac{1}{{\sqrt 3 }}\)\( \Rightarrow \) góc giữa (SIJ) và mặt phẳng (SAC) là \(\widehat {{\rm{OS}}E} = {30^0}\)






