1. Cho hàm số y = f(x) liên tục trên \(\left[ {a;b} \right]\) và có một nguyên hàm là hàm số F(x) trên \(\left[ {a;b} \right]\), a < c < b. Khẳng định nào sau đây sai:
A.\(\int\limits_a^b {f(x)dx = – \int\limits_b^a {f(x)dx.} } \)
B.\(\int {f'(x)dx = f(x) + C.} \)
C.\(\int\limits_a^b {f(x)dx = \int\limits_a^c {f(x)dx} + \int\limits_b^c {f(x)dx.} } \)
D.\(\int\limits_a^b {f(x)dx = F(b) – F(a)} .\)
2. Cho \(\int\limits_{ – 1}^2 {f(x)dx = 5;\int\limits_2^3 {f(x)dx = – 2.} } \) Tính \(\int\limits_{ – 1}^3 {f(x)dx?} \)
A. 7. B. -7.
C. 3. D.-3
3. Trong không gian Oxyz, cho hai mặt phẳng \((\alpha ):x + 2y + 4z – 1 = 0,\) \((\beta ):2x + 3y – 2z + 5 = 0.\) Chọn khẳng định đúng:
A.\((\alpha ) \bot (\beta ).\)
B.\((\alpha ),(\beta )\) chéo nhau.
C.\((\alpha )\parallel (\beta ).\)
D.\((\alpha ) \equiv (\beta ).\)
4. Khẳng định nào sau đây đúng:
A.\(\int\limits_a^b {udv = \left. {(uv)} \right|_a^b} – \int\limits_a^b {vdu} .\)
B.\(\int\limits_a^b {vdv = \left. {(uv)} \right|_a^b} – \int\limits_a^b {vdu} .\)
C.\(\int\limits_a^b {udv = \left. {(uv)} \right|_a^b} – \int\limits_a^b {udu} .\)
D.\(\int\limits_a^b {udx = \left. {(uv)} \right|_a^b} – \int\limits_a^b {vdx} .\)
5. Điểm nào sau đây thuộc đường thẳng \(\Delta :\left\{ \begin{array}{l}x = 1 + t\\y = 2 – t\\z = t\end{array} \right.\)?
A. M(0;-3;-1). B. M(3;0;2).
C. M(2;3;1). D. M(6;-3;2)
6. Hàm số \(f(x) = \sqrt {x + 3} \) là một nguyên hàm củ hàm số nào?
A.\(g(x) = \dfrac{2}{3}{(x + 3)^{\dfrac{3}{2}}} + C.\)
B.\(g(x) = \dfrac{1}{{2\sqrt {x + 3} }}.\)
C. \(g(x) = \dfrac{{ – 1}}{{\sqrt {x + 3} }}.\)
D.\(g(x) = \dfrac{3}{2}{(x + 3)^{\dfrac{3}{2}}} + C.\)
7. Trong không gian Oxyz, cho mặt phẳng \((\alpha ):2x + y – 3z + 1 = 0.\) Vectơ nào là vectơ pháp tuyến của mặt phẳng \((\alpha )?\)
A.\(\overrightarrow n (1;2;3).\)
B.\(\overrightarrow n ( – 2; – 1; – 3).\)
C.\(\overrightarrow n (2;1; – 3).\)
D.\(\overrightarrow n ( – 2;1; – 3).\)
8. Tìm \(F(x) = \int {\cos x.dx?} \)
A. sinx + C. B. cosx + C.
C. – cosx + C. D. – sinx + C.
9: Khẳng định nào sau đây là đúng?
A.\(\int {{2^x}dx = {2^x}} \ln 2 + C.\)
B.\(\int {\ln xdx = \dfrac{1}{x}} + C.\)
C.\(\int {{e^x}dx = – {e^x}} + C.\)
D.\(\int {{x^3}dx = \dfrac{{{x^4}}}{4}} + C.\)
10: Tính \(I = \int\limits_1^4 {({x^2} + 3\sqrt x } )dx.\)
A. 5,3. B. 35.
C. 3,5. D. 53.
11: Phần thực của số phức \(z = (a + i)(1 – i)\) là:
A. – a + 1. B. a – 1.
C. a + 1. D.\({a^2} + 1.\)
12: Trong không gian Oxyz, tính bán kính mặt cầu tâm I(1;0;0) và tiếp xúc với mặt phẳng (P): x – 2y + 2z + 2 = 0.
A.\(R = 3.\) B.\(R = 5.\)
C.\(R = \sqrt 2 .\) D.\(R = 1.\)
13: Cho z = 1 + 3i. Tính \(\dfrac{1}{z}.\)
A.\(\dfrac{1}{{10}} + \dfrac{3}{{10}}i.\) B.\(\dfrac{1}{{10}}i – \dfrac{3}{{10}}.\)
C.\(\dfrac{1}{{10}} – \dfrac{3}{{10}}i.\) D.\( – \dfrac{1}{{10}} – \dfrac{3}{{10}}i.\)
14: Trong không gian Oxyz, tính độ dài đoạn AB với A(1;-1;0), B(2;0;-2).
A. AB = 2. B.\(AB = \sqrt 3 .\)
C. AB = 6. D.\(AB = \sqrt 6 .\)
15: Trong không gian Oxyz, viết phương trình mặt phẳng (P) qua điểm \(M({x_0};{y_o};{z_o})\) và nhận \(\overrightarrow n (A;B;C)\) làm vectơ pháp tuyến?
A.\(A(x – {x_o}) + B(y – {y_o}) + C(z – {z_o}) \)\(\,= 0.\)
B.\(A(x + {x_o}) + B(y + {y_o}) + C(z + {z_o}) \)\(\,= 0.\)
C.\(A(x – {x_o}) + B(y – {y_o}) + C(z – {z_o}) \)\(\,= 1.\)
D.\(A(x + {x_o}) + B(y + {y_o}) + C(z + {z_o})\)\(\, = 1.\)
Advertisements (Quảng cáo)
16: Tính thể tích khối tròn xoay do hình phẳng giới hạn bởi các đường y = cosx, y = 0, x = 0, \(x = \pi \) quay quanh trục Ox.
A. 0.
B.\(2\pi .\)
C.\(\dfrac{{{\pi ^2}}}{2}.\)
D. 2.
17: Số phức liên hợp của số phức \(z = 7i + 2\) là:
A.\(\overline z = 7i – 2.\)
B.\(\overline z = 2 – 7i.\)
C.\(\overline z = – 2 – 7i.\)
D.\(\overline z = 2 + 7i.\)
18: Trong không gian Oxyz, cho \(\overline {OA} = \overrightarrow i – 2\overrightarrow j + 3\overrightarrow k .\) Tìm tọa độ điểm A.
A. A(-1;-2;-3). B. A(1;2;3).
C. A(1;-2;3). D. A(2;-4;6).
19: Trong không gian Oxyz vectơ nào là vectơ chỉ phương của đường thẳng \(d:\dfrac{{x – 1}}{2} = \dfrac{y}{1} = \dfrac{{z + 1}}{3}\)
A.\(\overrightarrow u = (2;1; – 3).\)
B.\(\overrightarrow u = \left( {1;\dfrac{1}{2};\dfrac{2}{3}} \right).\)
C.\(\overrightarrow u = \left( {1;\dfrac{1}{2};\dfrac{3}{2}} \right).\)
D.\(\overrightarrow u = \left( { – 4; – 2;6} \right).\)
20: Gọi \({z_1},{z_2}\) là hai nghiệm của phương trình \({z^2} + 3z + 3 = 0\) trên tập C. Tính \(T = \left| {{z_1}} \right| + \left| {{z_2}} \right|.\)
A.\(2\sqrt 3 .\) B.\(2\sqrt 5 .\)
C. 6. D.\(3\sqrt 2 .\)
21: Tìm tâm I và bán kính R của mặt cầu \((S):{x^2} + {y^2} + {z^2} – 2x – 4y + 2z + 2 \)\(\,= 0.\)
A.\(I( – 1; – 2;1),R = 2.\)
B.\(I(1;2; – 1),R = 2\sqrt 2 .\)
C.\(I( – 1; – 2;1),R = 2\sqrt 2 .\)
D.\(I(1;2; – 1),R = 2.\)
22: Đặt \(t = x +1\). Khi đó: \(\int\limits_0^1 {\dfrac{x}{{{{(x + 1)}^2}}}} dx = \int\limits_1^2 {f(t)dt.} \) Hàm số f(t) là hàm nào sau đây;
A.\(f(t) = \dfrac{{t – 2}}{{{t^2}}}.\)
B.\(f(t) = \ln \left| t \right| + \dfrac{1}{t}.\)
C.\(f(t) = \dfrac{1}{t} – \dfrac{1}{{{t^2}}}.\)
D.\(f(t) = \dfrac{1}{t} + \dfrac{1}{{{t^2}}}.\)
23: Môđun của số phức \(z = a – 2i\) là:
A.\(\left| z \right| = \sqrt {{a^2} + 4} .\)
B.\(\left| z \right| = \sqrt {{a^2} – 4} .\)
C.\(\left| z \right| = a + 2.\)
D.\(\left| z \right| = \sqrt {a + 2} .\)
24: Tìm phần thực và phần ảo của số phức \(z = 5 -4i.\)
A. Phần thực là 5, phầm ảo là 4i.
B. Phần thực là 5, phầm ảo là -4i.
Advertisements (Quảng cáo)
C. Phần thực là 5, phầm ảo là -4.
D. Phần thực là 5, phầm ảo là 4.
25: Trong không gian Oxyz, tính tọa độ trọng tâm g của tam giác ABC với A(1;-1;0), B(2;0;-2), C(0;-2;-4)?
A. \(G(1;-1;-2)\). B. \(G(1;-1;2).\)
C. \(G(-1;1;-2).\) D. \(G(-1;1;2).\)
26: Trong không gian với hệ tọa độ Oxyz, cho đường thẳng \(\Delta :\left\{ \begin{array}{l}x = – 1 + 3t\\y = 1 + t\\z = 3t\end{array} \right.\) và hai điểm A(5;0;2), B(2;-5;3). Tìm điểm M thuộc \(\Delta \) sao cho \(\Delta \)ABM vuông tại A.
A.M(2;2;3). B. M(5;3;6).
C. M(-4;0;-3). D. M(-7;-1;-6).
27: Cho khối cầu (S) có phương trình \({(x – 1)^2} + {(y – 2)^2} + {(z + 1)^2} = 25\), mặt phẳng (P) có phương trình x + 2y – 2z +5 = 0 cắt khối cầu (S) thành 2 phần. Tính thể tích của phần không chứa tâm của mặt cầu (S).
A.\(\dfrac{{25\pi }}{3}.\) B.\(\dfrac{{25\pi }}{6}.\)
C.\(\dfrac{{14\pi }}{3}.\) D.\(\dfrac{{16\pi }}{3}.\)
28: Trong không gian Oxyz, cho 2 điểm A(-2;1;3), B(3;-2;4), đường thẳng \(\Delta :\dfrac{{x – 1}}{2} = \dfrac{{y – 6}}{{11}} = \dfrac{{z + 1}}{{ – 4}}\) và mặt phẳng (P): 41x – 6y +54z + 49 = 0. Đường thẳng (d) đi qua B, cắt đường thẳng \(\Delta \) và mặt phẳng (P) lần lượt tại C và D sao cho thể tích của 2 tứ diện ABCO và OACD bằng nhau, biết (d) có một vectơ chỉ phương là \(\overrightarrow u = (4;b;c).\) Tính b + c.
A.11. B. 6.
C. 9. D. 4.
29: Biết \(\int\limits_0^a {x{e^x}} dx = 1(a > 0).\) Tìm a.
A. a = 1. B. a = 5.
C. a = 2. D. a = 3.
30: Trong không gian Oxyz, cho 3 điểm A(2;3;0),B(0;-4;1), C(3;1;1). Mặt cầu đi qua ba điểm A; B; C và có tâm I thuộc mặt phẳng (Oxz), biết I = (a;b;c). Tính tổng T = a + b + c.
A. T = 3. B. T = – 3.
C. T = 63. D. T = 69.
31: Biết \(\int\limits_0^{\dfrac{\pi }{4}} {\dfrac{{5 + 5{{\cos }^2}x + 6\sin 2x}}{{{{(2\sin x + 3\cos x)}^2}}}} dx = \dfrac{{a\pi + b}}{c}\) với a, b và c là các số nguyên dương. Tính tổng T = a + b + c.
A. \(T = 79.\) B. \(T = 36.\)
C. \(T = 63.\) D. \(T = 69.\)
32: Phương trình mặt phẳng đi qua điểm A(1;2;0) và chứa đường thẳng \(d:\dfrac{{x + 1}}{2} = \dfrac{y}{3} = \dfrac{z}{1}\) có một vectơ pháp tuyến là \(\overrightarrow n (1;a;b).\) Tính a + b.
A. a + b = 2. B. a + b = 0.
C. a + b = -3. D. a + b = 3.
33: Cho số phức z = a +bi \((a,b \in \mathbb{R})\)thỏa mãn \((1 + i)z + 2\overline z = 3 + 2i.\) Tính S = a + b
A.\(S = – \dfrac{1}{2}.\) B.\(S = 1.\)
C.\(S = \dfrac{1}{2}.\) D. \(S = – 1.\)
34: Trong không gian Oxyz, cho hai đường thẳng \({d_1}:\left\{ \begin{array}{l}x = 1 + t\\y = 2 – t\\z = 3t\end{array} \right.;{d_2}:\left\{ \begin{array}{l}x = 2s\\y = 1 – 2s\\z = 6s\end{array} \right..\) Chọn khẳng định đúng:
A.\({d_1},{d_2}\) chéo nhau.
B.\({d_1},{d_2}\) cắt nhau.
C.\({d_1}\parallel {d_2}\)
D.\({d_1} \equiv {d_2}.\)
35: Một nguyên hàm của hàm số: \(f(x) = {\sin ^2}x.co{s^3}x\) có dạng là: \(F(x) = – \dfrac{a}{b}{\sin ^5}x + \dfrac{c}{d}{\sin ^3}x,\) với \(\dfrac{a}{b}\) và \(\dfrac{c}{d}\) là các phân số tối giản, a;b;c;d là các số nguyên dương. Tính T = a + b + c + d.
A. Đáp án khác. B. T = 11.
C. T = 10. D. T = 9.
36: Trong không gian Oxyz, cho tứ diện ABCD có A(8;6;-7), B(2;-1;4), C(0;-3;0), D(-8;-2;9) và đường thẳng \(\Delta :\dfrac{{x + 2}}{2} = \dfrac{{y – 1}}{1} = \dfrac{{z – 3}}{2}.\) Mặt phẳng (P) chứa đường thẳng \(\Delta \) và cắt tứ diện ABCD thành 2 phần có thể tích bằng nhau, biết mặt phẳng (P) có một vectơ pháp tuyến \(\overrightarrow n = (7;b;c).\) Tính b + c.
A.8. B. 11.
C. 13. D. 9.
37: Đặt \(t = \sqrt {1 + \tan x} \) thì \(\int {\dfrac{{\sqrt {1 + \tan \,x} }}{{{{\cos }^2}x}}} dx\) trở thành nguyên hàm nào?
A.\(\int {2tdt.} \) B.\(\int {{t^2}dt.} \)
C.\(\int {dt.} \) D.\(\int {2{t^2}dt.} \)
38: Cho số phức z thỏa mãn \(\left| z \right| = 5\) và \(\left| {z + 3} \right| = \left| {z + 3 – 10i} \right|.\) Tìm số phức \({\rm{w}} = z – 4 + 3i.\)
A.\({\rm{w}} = – 1 + 7i.\) B.\({\rm{w}} = – 3 + 8i.\)
C.\({\rm{w}} = 1 + 3i.\) D.\({\rm{w}} = – 4 + 8i.\)
39: Trên tập số phức, tích 4 nghiệm của phương trình: \(x({x^2} – 1)(x + 2) = 24\) bằng:
A. -24. B. -12.
C. 12. D. 24.
40: Biết tích phân: \(\int\limits_0^{\dfrac{\pi }{6}} {\dfrac{1}{{1 + \sin }}} dx = \dfrac{{a\sqrt 3 + b}}{c},\) với a, b và c là các số nguyên. Tính tổng T = a + b + c.
A. T = 7. B. T = 11.
C.T = 5. D. T = 12.
41: Trong không gian Oxyz, cho mặt phẳng \((\alpha ):x + y – 2z + = 1 = 0\) đi qua M(1;-2;0), vuông góc và cắt đường thẳng \(d:\left\{ \begin{array}{l}x = 11 + 2t\\y = 2t\\z = – 4t\end{array} \right.\)tại N. Tính độ dài đoạn MN.
A.\(7\sqrt 6 .\) B.\(3\sqrt {11} .\)
C.\(\sqrt {10} .\) D.\(4\sqrt 5 .\)
42: Trong không gian Oxyz, cho A(2;3;-1); B(-1;1;1);C(1;m-1;2). Tìm m để tam giác ABC vuông tại B.
A. m = 1. B. m = 0.
C. m = 2. D. m = -3.
43: Cho số phức \({z_1} = a – 2i;{z_2} = 1 + bi\). Tìm phần ảo của số phức \(\overline z \), biết \({z_1}.z + {z_2}.z = 1 + i.\)
A.\(\dfrac{{a + b – 1}}{{{{(a + 1)}^2} + {{(b – 2)}^2}}}.\)
B.\(\dfrac{{a – b + 3}}{{{{(a + 1)}^2} + {{(b – 2)}^2}}}.\)
C.\(\dfrac{{b – a – 3}}{{{{(a + 1)}^2} + {{(b – 2)}^2}}}.\)
D.\(\dfrac{{1 – a – b}}{{{{(a + 1)}^2} + {{(b – 2)}^2}}}.\)
44: Biết \(\int\limits_2^3 {\dfrac{1}{{3x + 2}}} dx = m\ln 10 + n\ln 7;\) \((m,n \in \mathbb{Q}).\) Tính \(m – n.\)
A. 1. B.\(\dfrac{2}{3}.\)
C.\( – \dfrac{2}{3}.\) D. 0.
45: Diện tích hình phẳng giới hạn bởi hai đường \(y = {x^3} – x;y = 3x\) bằng:
A. 0. B. 8.
C. 16. D. 24.
46: Cho số phức z hỏa mãn điều kiện: \(\left| {z – 1 – 2i} \right| + \left| {\overline z – 3} \right| = \left| {\sqrt 7 + 3i} \right|.\) Tìm giá trị nhỏ nhất của \(P = \left| {z – 2 – i} \right|.\)
A. \(P = 2.\) B.\(P = \sqrt 2 .\)
C.\(P = \sqrt 3 .\) D. \(P = 3.\)
47: Biết \(\int {\left( {\dfrac{1}{{2x}} + {x^5}} \right)} dx = a\ln \left| x \right| + b{x^6} + C\) \((a,b \in \mathbb{Q},C \in \mathbb{R}).\) Tính \({a^2} + b?\)
A.\(\dfrac{7}{6}.\) B.\(\dfrac{7}{{13}}.\)
C.\(9.\) D.\(\dfrac{5}{{12}}.\)
48: Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P): x + 2y – 5z – 3 = 0 và hai điểm A(3;1;1), B(4;2;3). Gọi (Q) là mặt phẳng qua AB và vuông góc với (P). Phương trình nào là phương trình của mặt phẳng (Q).
A. \(9x – 7y – z + 19 = 0.\)
B. \(- 9x + 7y + z – 19 = 0. \)
C. \(- 9x – 7y + z – 19 = 0.\)
D. \(9x – 7y – z – 19 = 0. \)
49: Trong không gian với hệ tọa độ Oxyz, cho 2 đường thẳng \({\Delta _1}:\left\{ \begin{array}{l}x = 3 + t\\y = 1 + t\\z = 1 + 2t\end{array} \right.;\) \({\Delta _2}:\dfrac{{x + 2}}{2} = \dfrac{{y – 2}}{5} = \dfrac{z}{{ – 1}}\) và điểm M(0;3;0). Đường thẳng đi qua M, cắt \({\Delta _1}\) và vuông góc với \({\Delta _2}\) có một vectơ chỉ phương là \(\overrightarrow u = (4;a;b).\) Tính \(T = a + b.\)
A. \(T = -2.\) B. \(T = 4.\)
C. \(T = -4.\) D. \(T = 2.\)
50: Diện tích hình phẳng (phần gạch chéo) giới hạn bởi đồ thị 3 hàm số f(x), g(x) và h(x) như hình bên, bằng kết quả nào sau đây.
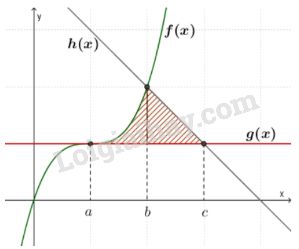
A.\(S = \int\limits_a^c {\left| {f(x) – g(x)} \right|} dx \)\(\,+ \int\limits_b^c {\left| {g(x) – h(x)} \right|} dx.\)
B.\(S = \int\limits_a^b {\left[ {f(x) – g(x)} \right]} dx \)\(\,+ \int\limits_b^c {\left[ {g(x) – h(x)} \right]} dx.\)
C.\(S = \int\limits_a^b {\left[ {f(x) – g(x)} \right]} dx \)\(\,- \int\limits_b^c {\left[ {g(x) – h(x)} \right]} dx.\)
D.\(S = \int\limits_a^c {\left[ {f(x) + h(x) – g(x)} \right]} dx.\)
|
1 |
2 |
3 |
4 |
5 |
|
C |
C |
A |
A |
B |
|
6 |
7 |
8 |
9 |
10 |
|
B |
C |
A |
D |
B |
|
11 |
12 |
13 |
14 |
15 |
|
C |
D |
C |
D |
A |
|
16 |
17 |
18 |
19 |
20 |
|
C |
B |
C |
C |
A |
|
21 |
22 |
23 |
24 |
25 |
|
D |
C |
A |
C |
A |
|
26 |
27 |
28 |
29 |
30 |
|
A |
C |
D |
A |
C |
|
31 |
32 |
33 |
34 |
35 |
|
A |
B |
D |
C |
C |
|
36 |
37 |
38 |
39 |
40 |
|
C |
D |
D |
A |
C |
|
41 |
42 |
43 |
44 |
45 |
|
D |
B |
C |
B |
B |
|
46 |
47 |
48 |
49 |
50 |
|
B |
D |
D |
D |
C |
