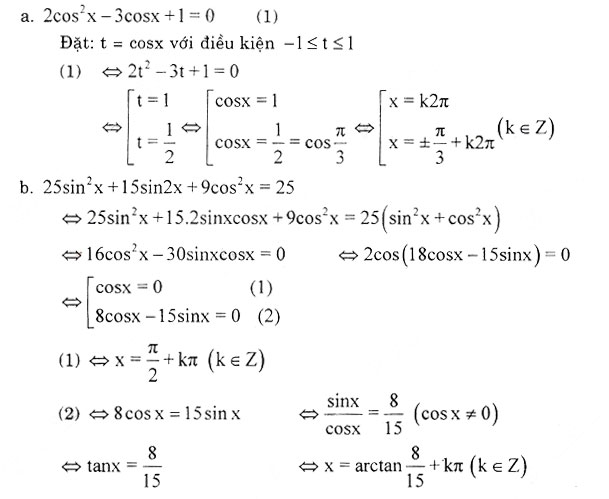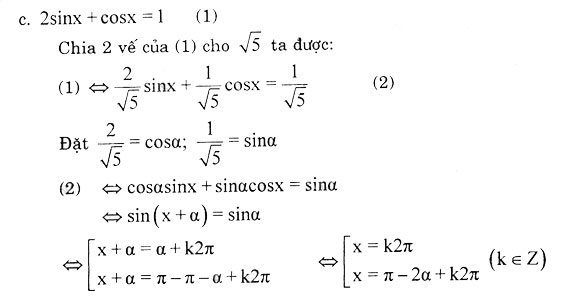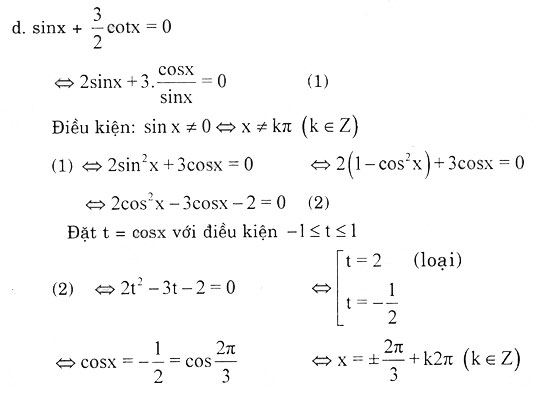Bài tập 1,2,3,4,5 ôn tập chương 1 Giải tích lớp 11

Đáp án và hướng dẫn giải bài 1,2,3,4,5 Ôn tập chương 1 Đại số, giải tích lớp 11: HÀM SỐ LƯỢNG GIÁC  VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC.

1. BÀI TẬP VỀ HÀM SỐ LƯỢNG GIÁC
2. BÀI TẬP VỀ PHƯƠNG TRÌNH LƯỢNG GIÁC CƠ BẢN
3. BÀI TẬP VỀ MỘT SỐ PHƯƠNG TRÌNH LƯỢNG GIÁC

Bài 1. a. Hàm số y = cos3x có phải là hàm số chẵn không? Tại sao?

b. Hàm số y = tan ( x+ π/5) có phải là hàm số lẻ  không? Tại sao?

Giải: a. Hàm số y = cos3x là hàm số chẵn vì:

TXĐ: D = R. ∀x ∈ D ta có  -x ∈ D. Xét: f (-x) = cos(-3x) = cos3x = f(x) ∀x ∈ D.

b. Hàm số y = tan ( x+ π/5) không phải là hàm số lẻ vì:

f (-x) = tan ( – x+ π/5) ≠ tan ( – x – π/5) = -f(x) ∀x ∈ D.

---

Bài 2. Căn cứ vào đồ thị hàm số y = sinx, tìm những giá trị của X trên đoạn [-3π/2;2π] để hàm số đó:

a. Nhận giá trị bằng -1

b. Nhận giá trị âm

Giải: Ta có đồ thị hàm số y= sinx

a. Dựa vào đồ thị hàm số, ta thấy trên đoạn [-3π/2;2π], để hàm số

y = sinx nhận giá trị bằng -1 thì X = -π/2 và X = 3π/2

b. Đồ thị y = sinx nhận giá trị âm trên đoạn [-3π/2;2π], trong các khoảng (-π,0) và  (π,2π)

---

Bài 3. Tìm giá trị lớn nhất của các hàm số sau:

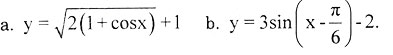
Giải: 

b. y = 3sinx(x -π/6)-2. Hàm số y = 3sinx(x -π/6)-2 đạt giá trị lớn nhất bằng 1 khi sinx(x -π/6) =1 (Vì  -1 ≤ (x -π/6) ≤ 1∀x ∈ D.

Ta có

y_max= 1 ⇔ sin(x – π/6) = 1  ⇔ x – π/6 = π/2 + k2π

x = 2π/3 + k2π (k ∈ Z)

---

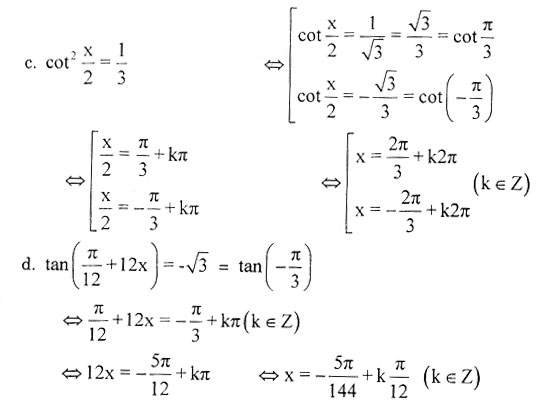
Bài 4. Giải các phương trình sau:

a) sin(x+1) = 2/3             b) sin²2x =1/2

c) cot²x/2 = 1/3              d) tan (π/12 + 12x) = – √3

Hướng dẫn giải bài 4 ôn tập chương 1.

---

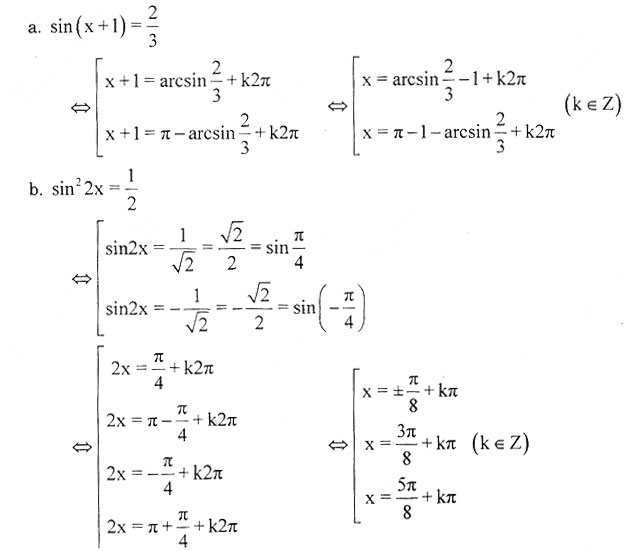
Bài 5. 2cos²x – 2cosx + 1 = 0

25sin²x + 15sin2x+ 9cos²x = 25

2sinx + cosx = 1

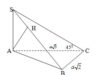
sinx + 1,5cotx = 0

Hướng dẫn giải bài 5: