Giải bài 1,2,3,4,5 trang 92 đại số giải tích 11: Dãy số

Dãy số – Chương 3 (Toán 11): Giải bài 1, 2, 3, 4, 5 trang 92 SGK đại số giải tích.

Bài 1. Viết năm số hạng đầu của các dãy-số có số hạng tổng quát u_n cho bởi công thức: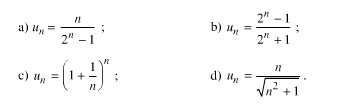

Năm số hạng đầu của dãy số là:

a)  u₁ = 1; u₂ = 2/3, u₃ = 3/7; u₄ =4/15; u₅ =5/31

b) u₁ = 1/3; u₂ = 3/5, u₃ = 7/9; u₄ =15/17; u₅ =31/33

c)  u₁ = 2; u₂ = 9/4, u₃ = 64/27; u₄ = 625/256; u₅ = 7776/3125

d) u₁ = 1/√2; u₂ = 2/√5, u₃ = 3/√10; u₄ =4/√17; u₅ =5/√26

Bài 2 trang 92 . Cho dãy-số U_n , biết:

u₁ = -1; u_n+1 = u_n +3 với n ≥ 1.

a) Viết năm số hạng đầu

b) Chứng minh bằng phương pháp quy nạp: u_n = 3n -4.

HD.a) Năm số hạng đầu  là -1, 2, 5, 8, 11.

b) Chứng minh u_n  = 3n – 4 bằng phương pháp quy nạp:

Với n =1 thì u₁ 3.1 – 4 = -1, đúng.

Giả sử hệ thức đúng với n = k ≥ 1, tức là u_k = 3k -4. Ta chứng minh hệ thức cũng đúng với n = k + 1.

Thật vậy, theo công thức của Dãysố và giả thiết quy nạp, ta có:

u_k+1 =  u_k + 3 = 3k – 4 + 3 = 3(k + 1) – 4.

Vậy hệ thức đúng với mọi n ∈ N^*  , tức là công thức đã được chứng minh.

Bài 3 trang 92 . Dãysố u_n cho bởi: u₁ = 3; , n ≥ 1.

a) Viết năm số hạng đầu

b) Dự đoán công thức số hạng tổng quát và chứng minh côngt hức đó bằng phương pháp quy nạp

HD. a) Năm số hạng đầu của dãysố là 3, √10, √11, √12, √13.

b) Ta có:  u₁ = 3 = √9 = √(1 + 8)

u₂ = √10 = √(2 + 8)

u₃ = √11 = √(3 + 8)

u₄ = √12 = √(4 + 8)

…….

Từ trên ta dự đoán u_n = √(n + 8), với n ∈ N^*  (1)

Chứng minh công thức (1) bằng phương pháp quy nạp:

– Với n = 1, rõ ràng công thức (1) là đúng.

– Giả sử (1) đúng với n = k ≥ 1, tức là có  u_k = √(k + 8) với k ≥ 1.

Theo công thức dãysố, ta có:   

Như vậy công thức (1) đúng với n = k + 1.

Vậy công thức (1) được chứng minh.

Bài 4. Xét tính tăng, giảm của các dãysố u_n biết:

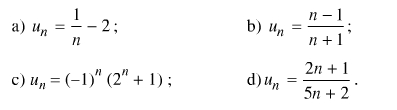
a)

Vậy dãy-số đã cho là giảm.

b) Xét hiệu

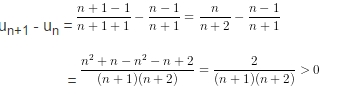
Vậy u_n+1 > u_n với mọi n ε N^* hay dãy số đã cho là tăng.

c) Các số hạng ban đầu vì có thừa số (-1)ⁿ, nên dãy-số không tăng và cũng không giảm.

d) Làm tương tự như câu a) và b) hoặc lập tỉ số u_{n+1 /} u_n
(vì u_n > 0  với mọi n ε N^* ) rồi so sánh với 1.

Ta có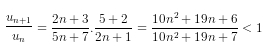 với mọi n  N^*

Vậy dãy số đã cho là giảm dần.

Bài 5. Trong các dãy số sau, bị chặn dưới, bịchặn trên, bị chặn?

a) Dãy số bị chặn dưới vì u_n = 2n² -1 ≥ 1 với mọi n ε  N^*   và không bịchặn trên vì với số M dương lớn bất kì, ta có 2n² -1 > M ⇔

Do đó n(n + 2) =  n² + 2n ≥ 3, suy ra

c) Vì n ≥ 1 nên 2n² – 1 > 0, suy ra

Mặt khác n² ≥ 1 nên 2n² ≥ 2 hay 2n² – 1≥ 1, suy ra