Bài 1,2,3,4,5 trang 82,83 SGK đại số và giải tích 11: Phương pháp quy nạp toán học

Tóm tắt lý thuyết và Giải bài 1,2,3 trang 82; Bài 4,5 trang 83 SGK đại số và giải tích 11: Phương pháp quy nạp toán học. Đây là bài đầu tiên Chương 3 Đại số và giải tích lớp 11: Dãy số – cấp số cộng cấp số nhân.

A. Tóm tắt lý thuyết

1. Để chứng minh một mệnh đề P(n) là đúng với mọi n ∈ N^*, ta thường dùng phương pháp quy nạp toán học, được tiến hành theo hai bước như sau:

Bước 1 (bước cơ sở): Kiểm tra mệnh đề P(n) đúng với n = 1.

Bước 2 ( bước quy nạp): Giả thiết mệnh đề P(n) đúng với một số tự nhiên bất kì n = k, (k ≥ 1) (ta gọi là giả thiết quy nạp) và chứng minh rằng nó cũng đúng với n = k + 1.

Khi đó, theo nguyên lí quy nạp toán học, ta kết luận mệnh đề P(n) đùng với mọi n ∈ N^* 

2. Trong trường hợp phải chứng minh một mệnh đề P(n) lf đúng vơi mọi số tự nhiên n ≥ p (p là số tự nhiên) thì:

– Ở bước 1, ta kiểm tra mệnh đề P(n) đúng với n = p.

Ở bước 2, ta giả thiết mệnh đề P(n) đúng với một số tự nhiên bất kì n = k, (k ≥ p) và chứng minh rằng nó cũng đúng với n = k + 1.

3. Phép thử với một số hữu hạn số tự nhiên tuy không phải là chứng minh nhưng cho phép ta dự đoán được kết quả. Kết quả này chỉ là giá thuyết và để chứng minh ta có thể dùng phương pháp quy nạp toán học.

Một số bài toán thường gặp

– Chứng minh các mệnh đề toán học liên quan đến lập luận lôgic.

– Chứng minh các đẳng thức, bất đẳng thức.

– Dự đoán kết quả và chứng minh.

B. Giải bài tập sách giáo khoa bài phương pháp quy nạp toán học – Sách giáo khoa đại số giải tích lớp 11 trang 82,83

Bài 1. Chứng minh rằng với n ∈ N^*, ta có đẳng thức:

a) Với n = 1, vế trái chỉ có một số hạng là 2, vế phải bằng
(3+1) / 2 = 2

Vậy VT = VP hệ thức a) đúng với n = 1.

Đặt vế trái bằng  S_n.

Giả sử đẳng thức a) đúng với n = k ≥ 1, tức là

Ta phải chứng minh rằng a) cũng đúng với n = k + 1, nghĩa là phải chứng minh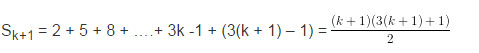

Thật vậy, từ giả thiết quy nạp, ta có: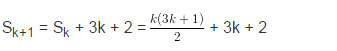 

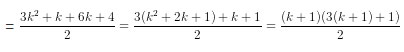
(điều phải chứng minh)

Vậy theo nguyên lí quy nạp toán học, hệ thức a) đúng với mọi n ∈ N^*

b) Với n = 1, vế trái bằng 1/2, vế phải bằng 1/2, do đó hệ thức đúng.

Đặt vế trái bằng S_n.

Giả sử hệ thức b) đúng với n = k ≥ 1, tức là

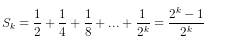
Ta phải chứng minh

Thật vậy, từ giả thiết quy nạp, ta có:

(điều phải chứng minh)

Vậy theo nguyên lí quy nạp toán học, hệ thức b) đúng với mọi n ∈ N^*

c) Với n = 1, vế trái bằng 1, vế phải bằng 1(1+1)(2+1) / 6 = 1 nên hệ thức c) đúng với n = 1.

Đặt vế trái bằng S_n.

Giả sử hệ thức c) đúng với n = k  ≥ 1, tức là

Ta phải chứng minh

Thật vậy, từ giả thiết quy nạp ta có:

(đpcm)

Vậy theo nguyên lí quy nạp toán học, hệ thức c) đúng với mọi n ∈ N^*

Bài 2. Chứng minh rằng với n ε  N^*    ta luôn có:

a) n³ + 3n² + 5n chia hết cho 3;

b) 4ⁿ + 15n – 1 chia hết cho 9;

c) n³ + 11n chia hết cho 6.

Đáp án: a) Đặt S_n = n³ + 3n² + 5n

Với n = 1 thì S₁ = 9 chia hết cho 3

Giả sử với n = k ≥ 1, ta có S_k = (k³ + 3k² + 5k) ⋮ 3

Ta phải chứng minh rằng S_k+1 ⋮ 3

Thật vậy S_k+1 = (k + 1)³ + 3(k + 1)² + 5(k + 1)

= k³  + 3k² + 3k + 1 + 3k² + 6k + 3 + 5k + 5

= k³ + 3k² + 5k + 3k² + 9k + 9

hay S_k+1 = S_k + 3(k² + 3k + 3)

Theo giả thiết quy nạp thì S_k⋮3, mặt khác 3(k² + 3k + 3) ⋮3 nên S_k+1 ⋮ 3.

Vậy (n³ + 3n² + 5n) ⋮ 3 với mọi n ∈ N^{*  .}

b) Đặt S_n = 4ⁿ + 15n – 1

Với n = 1, S₁ = 4¹ + 15.1 – 1 = 18 nên S₁ ⋮9

Giả sử với n = k ≥ 1 thì S_k= 4^k + 15k – 1 chia hết cho 9.

Ta phải chứng minh S_k+1 ⋮ 9.

Thật vậy, ta có: S_k+1 = 4^{k + 1} + 15(k + 1) – 1

= 4(4^k + 15k – 1) – 45k + 18 = 4S_k – 9(5k – 2)

Theo giả thiết quy nạp thì  Sk ⋮ 9  nên 4S₁ ⋮ 9, mặt khác 9(5k – 2)  ⋮ 9, nên S_k+1 ⋮ 9

Vậy (4ⁿ + 15n – 1) ⋮ 9 với mọi n ∈ N^*  

c) Đặt S_n = n³ + 11n

Với n = 1, ta có S₁ = 1³ + 11n = 12 nên S₁ ⋮ 6

Giả sử với n = k ≥ 1 ,ta có S_k = k³ + 11k ⋮ 6

Ta phải chứng minh S_k+1 ⋮ 6

Thật vậy, ta có S_k+1 = (k + 1)3 + 11(k + 1) =  k³ + 3k + 3k + 1 + 11k + 11

= ( k³ + 11k) + 3(k² + k + 4) = S_k + 3(k² + k + 4)

THeo giả thiết quy nạp thì  Sk ⋮ 6, mặt khác k² + k + 4 = k(k + 1) + 1 là số chẵn nên 3(k² + k + 4) ⋮ 6, do đó S_k+1 ⋮ 6

Vậy n³ + 11n chia hết cho 6 với mọi n ∈ N^*

Bài 3 Chứng minh rằng với mọi số tự nhiên n ≥ 2, ta có các bất đẳng thức:

a) 3ⁿ > 3n + 1;                  b) 2^{n + 1} > 2n + 3

Đáp án: a) Dễ thấy bất đẳng thức đúng với n = 2

Giả sử bất đẳng thức đúng với n = k ≥ 2, tức là

3^k > 3k + 1    (1)

Nhân hai vế của (1) vơi 3, ta được:

3^{k + 1} > 9k + 3 ⇔ 3^{k + 1} > 3k + 4 + 6k -1.

Vì 6k – 1 > 0 nên

3^{k + 1} > 3k + 4 hay 3^{k + 1} > 3(k + 1) + 1.

tức là bất đẳng thức đúng với n = k + 1.

Vậy 3ⁿ > 3n + 1 với mọi số tự nhiên n ≥ 2.

b) Với n = 2 thì vế trái bằng 8, vế phải bằng 7. Vậy bất đẳng thức đúng với n = 2

Giả sử bất đẳng thức đúng với n = k ≥ 2, tức là

2^{k + 1}  > 2k + 3              (2)

Ta phải chứng minh nó cũng đúng với n= k + 1, nghĩa là phải chứng minh

2^{k + 2} > 2(k + 1) + 3 <=> 2^{k + 2} > 2k + 5

Nhân hai vế của bất đẳng thức (2) với 2, ta được:

2^{k + 2} > 4k + 6 ⇔ 2^{k + 2} > 2k +5 + 2k + 1.

Vì 2k + 1> 0 nên 2^{k + 2} > 2k + 5

Vậy 2^{n + 1} > 2n + 3 với mọi số tự nhiên n ≥ 2.

Bài 4. Cho tổng  với n ∈ N^* 

a) Tính S₁, S₂, S_3.

b) Dự đoán công thức tính tổng S_n và chứng minh bằng quy nạp.

Giải: a) Ta có:

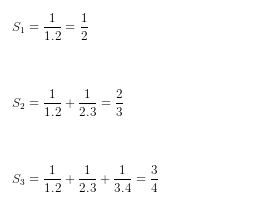
b) Từ câu a) ta dự đoán Sn=n/(n+1) (1), với mọi n ∈ N^{* .}

Ta sẽ chứng minh đẳng thức (1) bằng phương pháp quy nạp

Khi n = 1, vế trái là S1 =1/2, vế phải bằng  1/(1+1)=1/2. Vậy đẳng thức (1) đúng.

Giả sử đẳng thức (1) đúng với n = ≥ 1, tức là                 Ta phải chứng minh nó cũng đúng khi n = k + 1, nghĩa là phải chứng minh                  Ta có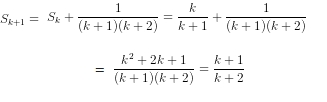

tức là đẳng thức (1) cũng đúng với n = k + 1.

Vậy đẳng thức (1) đã được chứng minh.

Bài 5 trang 83. Chứng minh rằng số đường chéo của một đa giác lồi n cạnh là

Giải: Ta chứng minh khẳng định đúng với mọi n ∈ N^*  ,  n ≥ 4.

Với n = 4, ta có tứ giác nên nó có hai đường chéo.

Mặt khác thay n = 4 vào công thức, ta có số đường chéo của tứ giác theo công thức là:   4(4-3)/2 = 2

Vậy khẳng định là đúng với n= 4.

Giả sử khẳng định là đúng với n = k ≥ 4, tức là đa giác lồi k cạnh có số đường chéo là  k(k – 3)/2

 Ta phải chứng minh khẳng định đúng với n = k + 1. Nghĩa là phải chứng minh đa giác lồi k + 1cạnh có số đường chéo là Xét đa giác lồi k + 1 cạnh