Đề kiểm tra 15 phút lớp 9 môn Toán Chương 3 Đại số: Xác định m để cặp số (1;m + 2) là một nghiệm của phương trình

Bài 1: Viết công thức nghiệm tổng quát và vẽ đường thẳng biểu diễn tập nghiệm của phương trình

\(x + 2y = −4.\)

Bài 2: Cho phương trình \(x – y = 2.\)

a) Xác định m để cặp số \(\left( {1;m + 2} \right)\) là một nghiệm của phương trình.

b) Cặp số \(\left( {\sqrt 2  + 1;\sqrt 2  – 1} \right)\) có phải là một nghiệm của phương trình hay không?

Bài 1: Ta có : \(x + 2y =  – 4 \Leftrightarrow y =  – {1 \over 2}x – 2\)

Vậy công thức nghiệm tổng quát là : \((x;- {1 \over 2}x – 2)\)

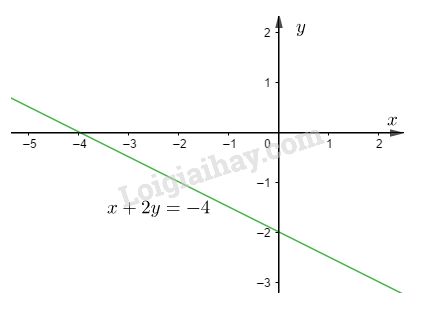
Vẽ đường thẳng \(y =  – {1 \over 2}x – 2\)

Bảng giá trị :

Đường thẳng qua hai điểm \(( 0; −2)\) và \((−4; 0).\)

Bài 2: a) Thế \(x = 1; y = m + 2\) vào phương trình \(x – y = 2\), ta được:

\(1 – \left( {m + 2} \right) = 2 \Rightarrow m =  – 3.\)

b) Thế \(x = \sqrt 2  + 1;y = \sqrt 2  – 1\) vào phương trình \(x – y = 2\), ta được :

\(\sqrt 2  + 1 – \left( {\sqrt 2  – 1} \right) = 2 \Leftrightarrow 2 = 2\) (đúng)

Vậy cặp số \(\left( {\sqrt 2  + 1;\sqrt 2  – 1} \right)\) là một nghiệm của phương trình.