Bài 1,2,3 trang 43 SGK giải tích lớp 12 (Khảo sát sự biến thiên và vẽ đồ thị của các hàm số)

Giải bài 1,2,3 trang 43 SGK giải tích lớp 12. Bài : Khảo sát sự biến thiên và vẽ đồ thị của các hàm số – Chương 1: Ứng dụng đạo hàm để khảo sát và vẽ đồ thị hàm số.

Bài 1. Khảo sát sự biến thiên và vẽ đồ thị của các hàm số bậc ba sau:

a) y = 2 + 3x – x³ ;                              b) y = x³ + 4x² + 4x ;

c) y = x³ + x²+ 9x ;                              d) y = –2x³ + 5 ;

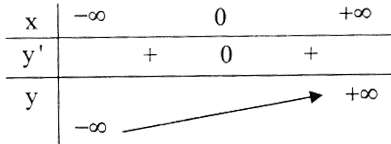
Đáp án: a) Tập xác định: R; y’ = 3(1 – x²); y’ = 0 ⇔ x = ± 1 .

Bảng biếnthiên :

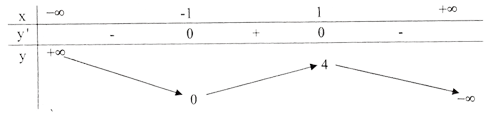
Đồ thị như hình bên.

b) Tập xác định : R ; y’ = 3x² + 8x + 4; y’ = 0 ⇔ x= -2, x =  -2/3 .

Bảng biếnthiên :

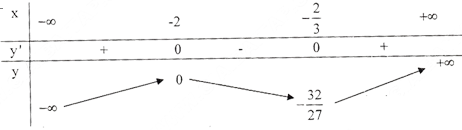
Vẽ đồ thị:

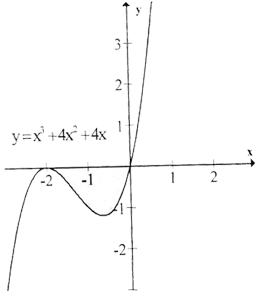
c) Tập xác định : R ;

y’ = 3x² + 2x + 9 > 0,  ∀x. Vậy hàm số luôn đồng biến, không có cực trị.

Bảng biếnthiên :

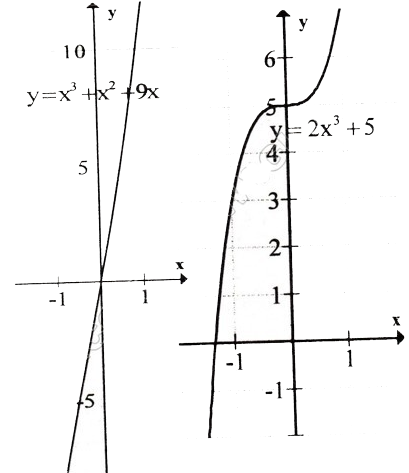Đồ thị câu 1 c,d

d) Tập xác định : R ;

y’ = -6x² ≤ 0,  ∀x. Vậy hàm số luôn nghịch biến, không có cực trị.

Bảng biến-thiên :

---

Bài 2. Khảo sát sự biến thiên và vẽ đồ thị của các hàm số bậc bốn sau:

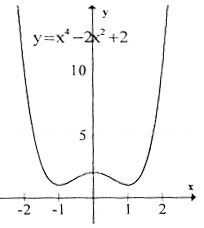
a) y = -x⁴ + 8x² – 1 ;               b) y = x⁴ – 2x² + 2 ;

c) y=  1/2x⁴   + x2– 3/2 ;           d) y = –2x² – x⁴ + 3 .

Đáp án: a) Tập xác định : R ; y’ =-4x³ + 16x = -4x(x² – 4);

y’ = 0  ⇔ x = 0, x = ±2 .

Bảng biếnthiên :

vẽ đồ thị

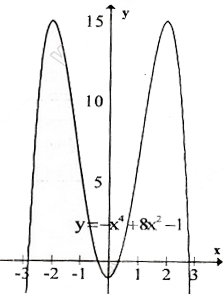
b) Tập xác định : R ; y’ =4x³ – 4x = 4x(x² – 1);

y’ = 0  ⇔ x = 0, x = ±1 .

Bảng biến-thiên :

Đồ thị như hình bên.

c) Tập xác định : R ; y’ =2x³ + 2x = 2x(x² + 1); y’ = 0  ⇔ x = 0.

Bảng biếnthiên :

Đồ thị như hình bên.

d) Tập xác định : R ; y’ = -4x – 4x³ = -4x(1 + x²); y’ = 0  ⇔ x = 0.

Bảng biến thiên :

---

Bài 3. Khảo sát sự biến thiên và vẽ đồ thị của các hàm số phân thức:

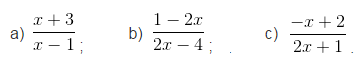
Tập xác định : R\{1};        Tiệm cận đứng : x = 1 . Tiệm cận ngang : y = 1.

Bảng biến thiên :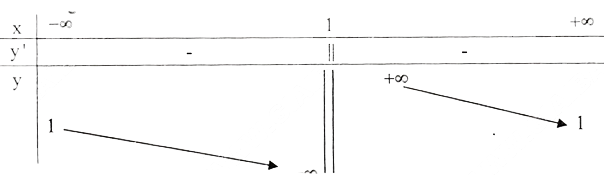

Đồthị như hình bên.

Giao điểm của đồ thị với trục tung: (0;-3), với trục hoành (-3;0). Môt số điểm của đồ thị (2;5), (3;3)

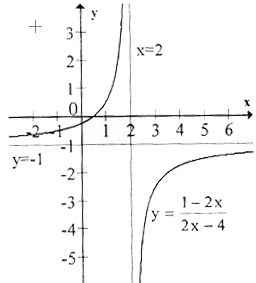
b) Tập xác định : R \{2};        Tiệm cận đứng : x = 2 . Tiệm cận ngang : y = -1.

Bảng biến thiên :

Đồthị:

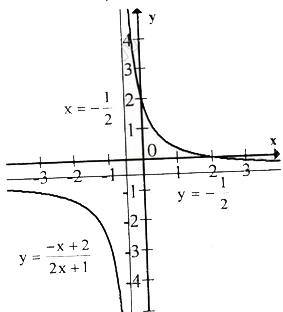
c) Tập xác định : R\{-1/2};       Tiệm cận đứng : x = -1/2 . Tiệm cận ngang : y = -1/2 .

Bảng biến thiên :

vẽ đồthị