Kiểm tra 15 phút Toán Chương 2 Hình học 9: Tính OH, AP theo R?

Cho điểm P nằm ngoài đường tròn (O; R) và \(OP = 2R.\) Một đường thẳng qua P cắt (O) tại A và B ( A nằm giữa B và P) và \(AB = R.\) Gọi H là chân đường vuông góc kẻ từ O đến PB.

a. Tính OH, AP theo R.

b. Kẻ một đường thẳng khác qua P cắt (O) tại C và D (CD ở khác phía với AB so với OP), kẻ \(OK ⊥ CD.\) So sánh AB và CD biết \(OK < {{R\sqrt 3 } \over 2}\)

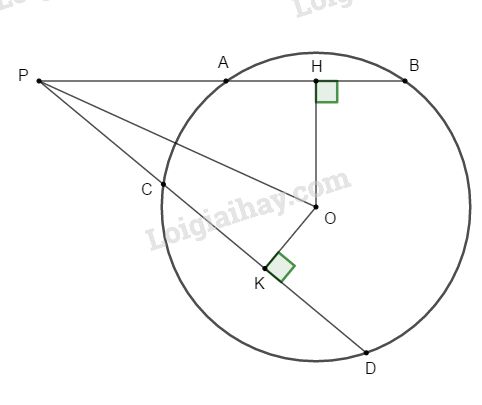
a. Ta có: \(OH ⊥ AB\) (gt)

\( \Rightarrow HA = HB = {{AB} \over 2} = {R \over 2}\)

(định lí đường kính dây cung)

Xét tam giác vuông AHO, ta có:

\(OH = \sqrt {A{O^2} – A{H^2}}  \)\(\;= \sqrt {{R^2} – {{\left( {{R \over 2}} \right)}^2}}  = {{R\sqrt 3 } \over 2}\)

∆PHO vuông tại H, ta có:

\(\eqalign{  & PH = \sqrt {P{O^2} – O{H^2}} \cr& = \sqrt {{{\left( {2R} \right)}^2} – {{\left( {{{R\sqrt 3 } \over 2}} \right)}^2}}  = {{R\sqrt {13} } \over 2}  \cr  &  \Rightarrow PA = PH – AH \cr&= {{R\sqrt {13} } \over 2} – {R \over 2} = {{R\left( {\sqrt {13}  – 1} \right)} \over 2} \cr} \)

b. \(OK < {{R\sqrt 3 } \over 2}\) hay \(OK < OH = {{R\sqrt 3 } \over 2}\,\left( {cmt} \right)\)

\(\Rightarrow AB < CD\)