PHÒNG GD&ĐT QUẬN BA ĐÌNH
ĐỀ KIỂM TRA HỌC KỲ II
MÔN TOÁN 9
NĂM HỌC 2017 – 2018
Thời gian làm bài: 120 phút
Bài I (2.0đ). Cho biểu thức A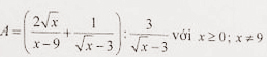
1) Rút gọn biểu thức A
2) Tìm x để A = 5/6
3) Tìm giá trị nhỏ nhất của biểu thức A
Bài II (2,0 đ):
1) Giải hệ phương trình: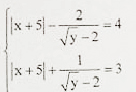
2) Giải bài toán bằng cách lập phương trình hoặc hệ phương trình.
Hai đội công nhân cùng làm một công việc thì làm xong trong 8 giờ. Nếu mỗi đội làm riêng một mình xong công việc đó, đội thứ nhất cần ít thời gian hơn so với đội thứ hai là 12 giờ. Hỏi mỗi đội làm một mình xong công việc đó trong bao lâu?
Advertisements (Quảng cáo)
Bài III (2,0 đ) Cho phương trình x2 – 2 (m + 1)x + m2 = 0
a) Giải phương trình khi m = 4
b) Tìm m để phương trình có hai nghiệm phân biệt x1; x2 sao cho x12 + x22 = 4 √x1x2
Bài IV (3,5 đ): Cho tam giác ABC có ba góc nhọn nội tiếp đường tròn tâm O bán kính R và AH là đường cao của tam giác ABC. Gọi M, N thứ tự là hình chiếu của H trên AB, AC
1) Chứng minh tứ giác AMHN là tứ giác nội tiếp
2) Chứng minh góc ABC = ANM
3) Chứng minh OA ⊥ MN
Advertisements (Quảng cáo)
4) Cho biết AH = R√2. Chứng minh M, O, N thẳng hàng.
Bài V (0,5 điểm). Cho a, b > 0 thỏa mã a + b ≤ 2.Tìm giá trị lớn nhất của biểu thức
P = √[a(b+1)] + √[b(a + 1)
Tham khảo thêm đề số 2 của huyện An Lão Hải Phòng năm 2018
1. Giải hệ phương trình và phương trình sau:
a) 
b) x2 + 7x = 0
2.a) Vẽ đồ thị (P) của hàm số y = -x2/2
b) Tìm những điểm thuộc (P) có hoành độ bằng 2 lần tung độ.
3. a) Cho phương trình x2 – (m + 5)x + 2m + 6 = 0 (x là ẩn số)
b) Chứng minh rằng: phương trình đã cho luôn luôn có hai nghiệm với mọi giá trị của m.
c) Tìm m để phương trình có hai nghiệm x1, x2 thỏa mãn: x12 + x22 = 35.
2.Hai ô tô cùng khởi hành từ A đến B dài 100 km, Vận tốc ô tô thứ nhất nhanh hơn ô tô thứ hai 10 km /h nên đến B trước ô tô thứ hai là 30 phút. Tính vận tốc của mỗi ô tô.
4. Cho đường tròn tâm O và điểm A nằm ngoài đường tròn đó. Vẽ các tiếp tuyến AB,AC và cát tuyến ADE tới đường tròn ( B và C là tiếp điểm). Gọi H là trung điểm của DE.
a) Chứng minh rằng tứ giác ABHO nội tiếp đường tròn.
b) Chứng minh rằng HA là tia phân giác của góc BHC
c) BH cắt đường tròn (O) ở K. Chứng minh rằng: AE // CK.
5. Cho các số thực dương x, y , z thỏa mãn x + y + z = 4.
Chứng minh rằng 1/xy + 1/xz ≥ 1
