
Cho nửa đường tròn (O), đường kính AB và một dây cung CD. Vẽ AP và BS vuông góc với CD. Chứng minh:
a. P và S ở bên ngoài đường tròn.
b. \(PC = DS\)

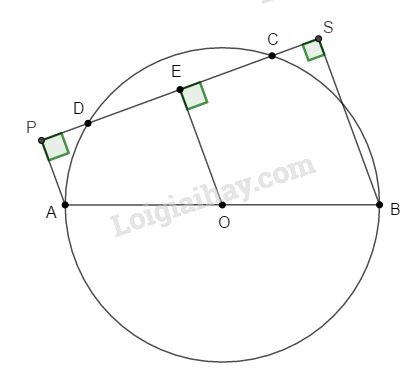
a. Ta có: AP // BS (⊥ CD) nên tứ giác APSB là hình thang vuông.
Kẻ \(OE ⊥ CD.\) Khi đó OE là đường trung bình của hình thang nên \(EP = ES.\)
Advertisements (Quảng cáo)
Trong hình thang APSD có:
\(\widehat {OAP} + \widehat {OBS} = 180^\circ \)
và giả sử \(\widehat {OAP} \ge 90^\circ ,\)
Xét ∆PAO ta có: \(\widehat {PAO} > \widehat {APO} \Rightarrow OP > AO\)
Advertisements (Quảng cáo)
mà AO là bán kính, do đó P nằm ngoài (O).
Mặt khác \(EP = ES\) (cmt)
\(⇒ SO = PO > OA\) nên S nằm ngoài (O)
b. Ta có: \(CE = DE\) (định lí đường kính dây cung)
và \(EP = ES\) (cmt)
\(⇒ EP – CE = ES – DE\) hay \(PC = DS\).



![[Tiếng Anh lớp 9 giữa học kì 2] có đáp án và lời giải năm học 2016 – 2017](https://dethikiemtra.com/wp-content/uploads/2015/08/mon-tieng-anh-lop-9-100x75.jpg)

