Từ điểm P nằm ngoài đường tròn (O; R), vẽ hai tiếp tuyến PA, PB (A, B là các tiếpđ). Gọi H là chân đường vuông góc kẻ từ A đến đường kính BC. Chứng minh rằng PC cắt AH tại trung điểm I của AH.
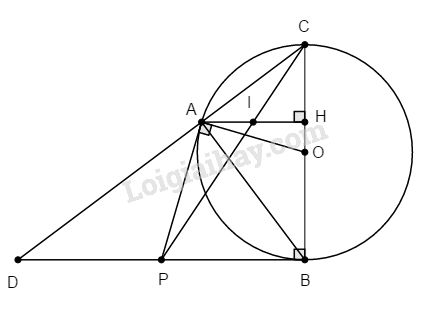
Gọi D là giao điểm của đường thẳng AC và BP.
Ta có: \(\widehat {BAC} = 90^\circ \) (BC là đường kính)
\( \Rightarrow \widehat {BAD} = 90^\circ \) (kề bù) hay \(\widehat {DAP} + \widehat {PAB} = 90^\circ \) (1)
∆ABD vuông tại A (cmt) \( \Rightarrow \widehat {ABD} + \widehat {ADB} = 90^\circ \) (2)
Advertisements (Quảng cáo)
Mặt khác PA, PB là hai tiếp tuyến cuả (O)
nên \(PA = PB\) và \(\widehat {PAB} = \widehat {PBA}\) (3)
Từ (1), (2) và (3) \( \Rightarrow \widehat {DAP} = \widehat {ADP}\)
Do đó ∆APD cân tại P
Advertisements (Quảng cáo)
\(⇒ PA = PD\), mà \(PA = PB\) (tính chất hai tiếp tuyến cắt nhau)
\(⇒ PD = PB.\)
Lại có DB // AH (⊥ BC)
Xét ∆PBC có : IH // PB \( \Rightarrow {{IH} \over {PB}} = {{IC} \over {PC}}\) (4) (Định lí Ta-lét)
Tương tự ∆PCD có : AI // PD \( \Rightarrow {{AI} \over {DP}} = {{IC} \over {PC}}\) (5)
Từ (4) và (5) \( \Rightarrow {{IH} \over {PB}} = {{AI} \over {DP}} \Rightarrow IH = IA\) (vì \(PB = PD\))
