Tam giác ABC có ba góc nhọn nội tiếp trong đường tròn (O). Đường tròn đường kính BC cắt AB, AC lần lượt tại E và F. BF, CE cắt nhau tại H.
a) Chứng minh H là trực tâm của tam giác ABC.
b) Gọi K là điểm đối xứng với H qua BC. Chứng minh tứ giác ABKC nội tiếp.
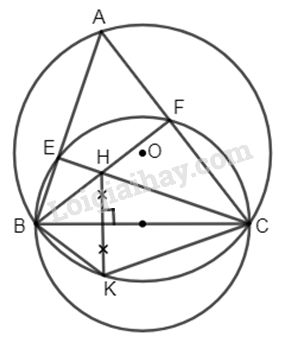
a) Ta có : \(\widehat {BEC} = 90^\circ \) ( BC là đường kính) hay \(CE \bot AB.\)
Advertisements (Quảng cáo)
Tương tự \(\widehat {BFC} = 90^\circ \) \( \Rightarrow BF \bot AC\) mà BF và CE cắt nhau tại H.
\( \Rightarrow \) H là trực tâm \(∆ABC.\)
b) H’ và H đối xứng qua BC
\(\Rightarrow BH = BK, CH = CK\)
Advertisements (Quảng cáo)
Từ đó hai tam giác BHC và BKC bằng nhau (c.c.c)
\(\left. \begin{gathered}
\Rightarrow \widehat {BKC} = \widehat {BHC} \hfill \\
\,\,\,\,\,\,\widehat {BHC’} = \widehat {EHF}\left( \text{đối đỉnh} \right) \hfill \\
\end{gathered} \right\} \Rightarrow \widehat {BKC} = \widehat {EHF}\)
Mặt khác tứ giác AEHF nội tiếp \(\left( {\widehat {AEH} + \widehat {AFH} = {{180}^o}} \right)\)
\( \Rightarrow \widehat A + \widehat {EHF} = {180^o}\)
Do đó \(\widehat A + \widehat {BKC} = {180^o}\). Vậy tứ giác ABKC nội tiếp.
