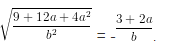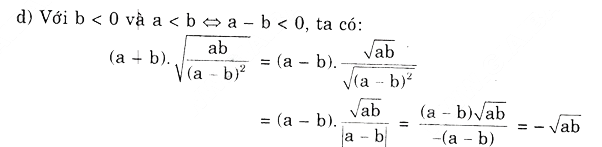Đáp án và hướng dẫn giải bài 28,29,30,31,32,33,34 trang 19 SGK Toán 9 tập 1: Liên hệ giữa phép chia và phép khai phương – Chương 1 Đại số lớp 9.
1. Định lí. Với số a không âm và số b dương ta có ![]() Lưu ý. a) Với biểu thức A ≥ 0 và B > 0 thì không thể viết đẳng thức trên. Chẳng hạn √-9/√-4 được xác định nhưng biểu thức √-9/√-4 không xác định.
Lưu ý. a) Với biểu thức A ≥ 0 và B > 0 thì không thể viết đẳng thức trên. Chẳng hạn √-9/√-4 được xác định nhưng biểu thức √-9/√-4 không xác định.
2. Quy tắc khai phương một thương
Muốn khai phương một thương a/b, trong đó a không âm, b dương, ta có thể khai phương lần lượt a và b rồi lấy kết quả thứ nhất chia cho kết quả thứ 2.
3. Quy tắc chia các căn bậc hai
Muốn chia các căn bậc hai của số a không âm cho căn bậc hai của số b dương ta có thể chia a cho cho b rồi khai phương kết quả đó.
Giải bài tập trong sách giáo khoa trang 19,20 Toán đại số lớp 9 tập 1
Bài 28. Tính:

Giải: a) √(289/225) =√289 / √225 = 17/15
 =√64/√25 = 8/5
=√64/√25 = 8/5
c)√0,25/9 = √25/900 = √25 / √900 = 5/30=1/6
d)√8,1/1,6 = √81/16 = √81 / √16 = 9/4
Bài 29.
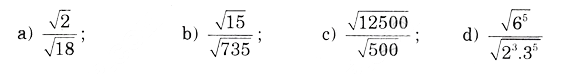
Đáp án: a) 1/3; b) 1/7; c) 5; d) 2.
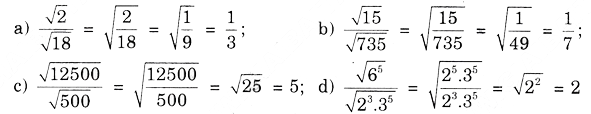
Bài 30. Rút gọn các biểu thức sau:

Advertisements (Quảng cáo)

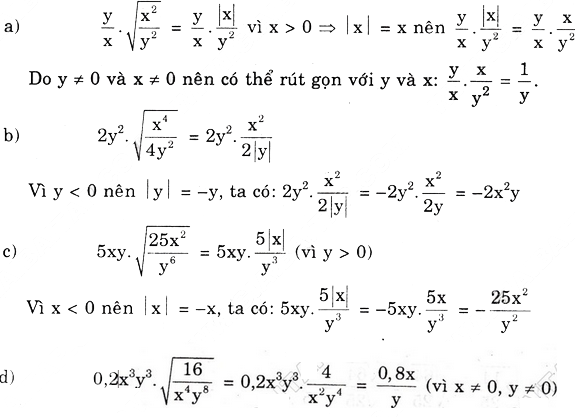
Bài 31. a) So sánh √25-16 và √25 – √16
b) Chứng minh rằng: với a > b >0 thì √a – √b < √a-b.

a) HD: Thực hiện phép khai căn rồi so sánh kết quả.
Trả lời: √(25-16) = √9 =3 ; √25 – √16 = 5-4=1 ⇒
√25-16 > √25 – √16;.
b) HD: Chứng minh √a – √b < √a-b Ta có thể chứng minh rằng √a < √a-b + √b (1)
Vì 2 vế của (1) là các số không âm và a>b, nên
(√a)2 = a; (2)
(√a-b + √b)2 =(√a – b)2 + 2√(a-b).b + (√b)2
= a- b + b + 2√(a-b).b= a+2√(a-b).b (3)
Advertisements (Quảng cáo)
So sánh (2) và (3) ta có (√a)2 < (√a-b + √b)2
⇒√a<√a-b + √b ⇒√a- √b< √a-b với a > b >0 (đpcm)
Bài 32. Toán 9.
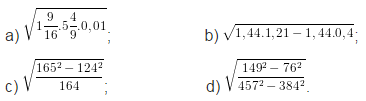
a) HD: Đổi hỗn số và số thập phân thành phân số.
ĐS: 7/24.



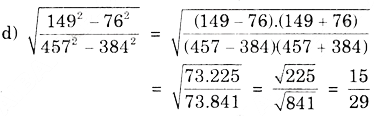
Bài 33.
a) √2.x – √50 = 0; b) √3.x + √3 = √12 + √27;
c) √3.x2 – √12 = 0; d) x2 /√5 – √20 = 0.
Giải: a) √2.x – √50 = 0 ⇔ √2.x = √50 ⇔ x = √50/√2 ⇔ x =√(50/2) = √25 = 5.
b) ĐS: x = 4.
⇔√3x + √3 = √4.3 + √9.3
⇔√3x + √3 = 2√3 + 3√3
⇔√3x + √3 = 5√3
⇔√3x = 4√3
⇔x=4
c)√3.x2 – √12 = 0
⇔ √3.x2 = √12 ⇔
x2= √12 / √3 ⇔ x2 = √12/3 ⇔ x2 = √4 ⇔ x2 = 2 ⇒x = √2 hoặc x = -√2.
d) ĐS: x = √10 hoặc x = -√10.
Bài 34. Rút gọn các biểu thức sau:


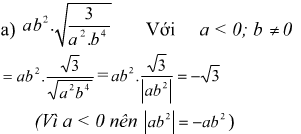

c) 
Vì b < 0 nên |b| = -b.
Vì a > -1,5 nên 3 + 2a > 0. Do đó = 3+ 2a.
Vậy