Giải bài tập 12,13,14, 15 trang 15; Bài 16,17, 18,19 trang 16 SGK Toán 9 tập 2: Giải hệ phương trình bằng phương pháp thế – Chương 3 Đại 9.
A. Tóm tắt lý thuyết Giải hệ phương trình bằng phương pháp thế
1. Quy tắc thế dùng để biến đổi một hệ phương trình thành hệ phương trình tương đương. Quy tắc thế gồm hai bước sau:
Bước 1: Từ một phương trình của hệ đã cho (coi là phương trình thứ nhất), ta biểu diễn một ẩn theo ẩn kia rồi thế vào phương trình thứ hai để được một phương trình mới (chỉ còn một ẩn).
Bước 2: Dùng phương trình mới để thay thế cho phương trình thứ hai trong hệ (và giữ nguyên phương trình thứ nhất).
2. Tóm tắt cách giải hệ phương trình bằng phương pháp thế.
Bước 1: Dùng quy tắc thế biến đổi hệ phương trình đã cho để được một hệ phương trình mới, trong đó có một phương trình một ẩn.
Bước 2: Giải phương trình một ẩn vừa có, rồi suy ra nghiệm của hệ đã cho.
3. Chú ý: Nếu thấy xuất hiện phương trình có các hệ số của hai ẩn đểu bằng 0 thì hệ phương trình đã cho có thể có vô số nghiệm hoặc vô nghiệm.
B. Giải bài tập Toán 9 tập 2 bài: Giải hệ phương trình bằng phương pháp thế trang 15,16.
Bài 12. Giải các hệ phương trình sau bằng phương pháp thế:
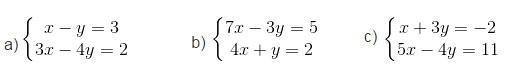
Hướng dẫn: a) Từ x – y = 3 ⇒ x = 3 + y.
Thay x = 3 + y vào phương trình 3x – 4y = 2.
Ta được 3(3 + y) – 4y = 2 ⇔ 9 + 3y – 4y = 2.
⇔ -y = -7 ⇔ y = 7
Thay y = 7 vào x = 3 + y ta được x = 3 + 7 = 10.
Vậy hệ phương trình có nghiệm (10; 7).
b) Từ 4x + y = 2 ⇒ y = 2 – 4x.
Thay y = 2 – 4x vào phương trình 7x – 3y = 5.
Ta được 7x – 3(2 – 4x) = 5 ⇔ 7x – 6 + 12x = 5.
⇔ 19x = 11 ⇔ x =11/19
Thay x =11/19 vào y = 2 – 4x ta được y = 2 – 4.11/19= 2 – 44/19
= -6/19
Hệ phương trình có nghiệm (11/9; -6/19)
c) Từ x + 3y = -2 ⇒ x = -2 – 3y.
Thay vào 5x – 4y = 11 ta được 5(-2 – 3y) – 4y = 11
⇔ -10 – 15y – 4y = 11
⇔ -19y = 21 ⇔ y = -21/19
Nên x = -2 -3(-21/19) = -2 + 63/19 = 25/19
Vậy hệ phương trình có nghiệm (25/19; – 21/19)
Bài 13. Giải các hệ phương trình sau bằng phương pháp thế:
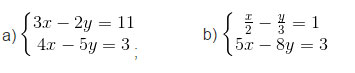
Giải: 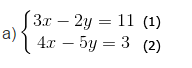
Từ phương trình (1) ⇒ 2y = 3x -11 ⇔![]()
Thế (3) vào y trong phương trình (2):
![]()
⇔ 8x -15x + 55 = 6 (Quy đồng mẫu số 2 vế)
⇔ -7x = -49 ⇔ x = 7.
Thế x = 7 vào (3) ta được ![]()
⇔ y = 5. Nghiệm của hệ phương trình đã cho là (7; 5)
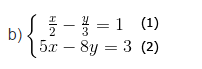
Từ phương trình (1) ⇒![]()
Thế (3) vào x trong phương trình (2):![]()
Advertisements (Quảng cáo)
⇔ 10y + 30 – 24y = 9 (Quy đồng mẫu số 2 vế)
⇔ -14y = -21 ⇔ y =3/2
Thế y = 3/2 vào (3) ta được
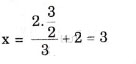
Vậy hệ phương trình có nghiệm (3;3/2).
Bài 14 trang 15. Giải các hệ phương trình bằng phương pháp thế: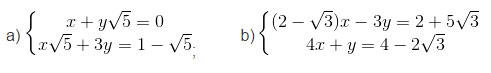
Giải: a) Từ phương trình thứ nhất ta có x = -y√5.
Thế vào x trong phương trình thứ hai ta được:
-y√5.√5+ 3y = 1 – √5
⇔ -2y = 1 – √5
⇔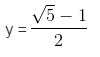
Từ đó: 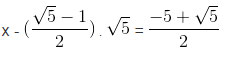
Vậy hệ phương trình có nghiệm: (x, y) = 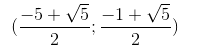
b) Từ phương trình thứ hai ta có y = 4 – 2√3- 4x.
Thế vào y trong phương trình thứ hai được
(2 -√3 )x – 3(4 – 2√3- 4x) = 2 + 5√3⇔ (14 – √3 )x = 14 – √3
⇔ x = 1
Từ đó y = 4 – 2√3- 4 . 1 = -2√3
Vậy hệ phương trình có nghiệm:(x; y) = (1; -2√3)
Bài 15 trang 15 Toán 9. Giải hệ phương trình 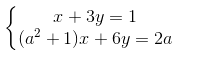
trong mỗi trường hợp sau:
a) a = -1; b) a = 0; c) a = 1.
Hướng dẫn: a) Khi a = -1, ta có hệ phương trình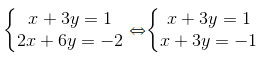
Hệ phương trình vô nghiệm.
b) Khi a = 0, ta có hệ 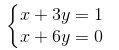
Từ phương trình thứ nhất ta có x = 1 – 3y.
Thế vào x trong phương trình thứ hai, được:
Advertisements (Quảng cáo)
1 – 3y + 6y = 0 ⇔ 3y = -1 ⇔ y = -1/3
Từ đó x = 1 – 3(-1/3) = 2
Hệ phương trình có nghiệm (x; y) = (2; -1/3).
c) Khi a = 1, ta có hệ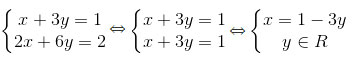
Hệ phương trình có vô số nghiệm.
Bài 16. Giải hệ phương trình
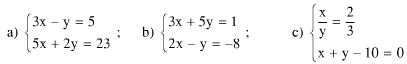
Đáp án: a)
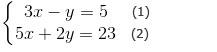
Từ phương trình (1) ⇔ y = 3x – 5 (3)
Thế (3) vào y trong phương trình (2): 5x + 2(3x – 5) = 23
⇔ 5x + 6x – 10 = 23 ⇔ 11x = 33 ⇔x = 3
Thay x = 3 vào (3) ta có y = 3.3 – 5 = 4.
Vậy hệ có nghiệm (x; y) = (3; 4).
b)
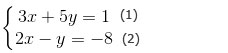
Từ phương trình (2) ⇔ 2x – y = -8 ⇔ y = 2x + 8 (3)
Thế (3) vào y trong phương trình (1): 3x + 5(2x + 8) = 1
⇔ 3x + 10x + 40 = 1 ⇔ 13x = -39
⇔ x = -3
Thay x = 3 vào (3) ta có y = 2(-3) + 8 = 2.
Vậy hệ có nghiệm (x; y) = (-3; 2).
c)
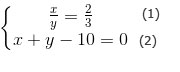
Phương trình (1) ⇔ x = 2/3y (3)
Thế (3) vào x trong phương trình (2): 2/3y + y = 10 ⇔ 5/3y = 10
⇔ y = 6.
Thay y = 6 vào (3) ta có x = 2/3. 6 = 4
Vậy nghiệm của hệ là (x; y) = (4; 6).
Bài 17 trang 16 Toán 9. Giải hệ phương trình sau bằng phương pháp thế.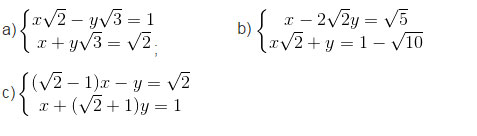 Hướng dẫn bài 17:
Hướng dẫn bài 17:
a) 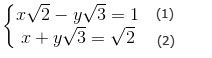
Từ phương trình (2) ⇔ x = √2 – y√3 (3)
Thế (3) vào (1): ( √2 – y√3)√2 – y√3 = 1
⇔ √3y(√2 + 1) = 1 ⇔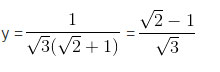
Từ đó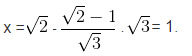
Vậy có nghiệm 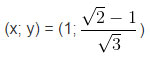
b) 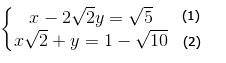
Từ phương trình (2) ⇔ y = 1 – √10 – x√2 (3)
Thế (3) vào (1): x – 2√2(1 – √10 – x√2) = √5
⇔ 5x = 2√2 – 3√5 ⇔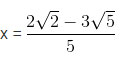
Từ đó 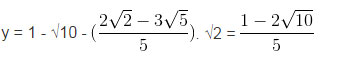
Vậy hệ có nghiệm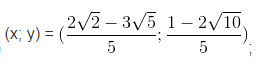
c) 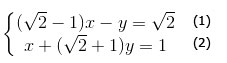
Từ phương trình (2) ⇔ x = 1 – (√2 + 1)y (3)
Thế (3) vào (1): (√2 – 1)[1 – (√2 + 1)y] – y = √2 ⇔ -2y = 1 ⇔ y = -1/2
Từ đó x = 1 – (√2 + 1)(-1/2) = (3+ √2)/2
Vậy hệ có nghiệm (x; y) = ( (3+ √2)/2; -1/2)
Bài 18. a) Xác định các hệ số a và b, biết rằng hệ phương trình
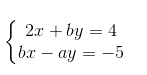
Có nghiệm là (1; -2)
b) Cũng hỏi như vậy, nếu hệ phương trình có nghiệm là (√2 – 1; √2).
Lời giải: a) Hệ phương trình có nghiệm là (1; -2) có nghĩa là xảy ra
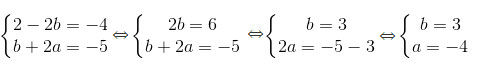
b) Hệ phương trình có nghiệm là (√2 – 1; √2),
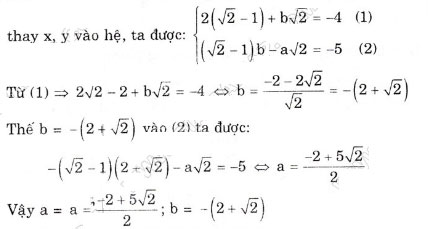
Bài 19. Biết rằng: Đa thức P(x) chia hết cho đa thức x – a khi và chỉ khi P(a) = 0.
Hãy tìm các giá trị của m và n sao cho đa thức sau đồng thời chia hết cho x + 1 và x – 3:
P(x) = mx3 + (m – 2)x2 – (3n – 5)x – 4n.
Giải: P(x) chia hết cho x + 1 ⇔ P(-1) = -m + (m – 2) + (3n – 5) – 4n = 0 hay -7 -n = 0 (1)
P(x) chia hết cho x – 3 ⇔ P(3) = 27m + 9(m – 2) – 3(3n – 5) – 4n = 0 hay 36m -13m = 3 (2)
Từ (1) và (2), ta có hệ phương trình ẩn m và n.
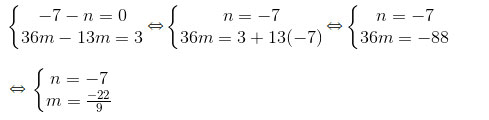

![[Lâm Đồng] kiểm tra học kì 2 Văn 9: Nhân vật nữ thanh niên xung phong trong truyện Những ngôi sao xa xôi](https://dethikiemtra.com/wp-content/uploads/2015/06/thcs-tinh-daklak-100x75.jpg)



