Bài 23,24 ,25,26 trang 17 sách Toán 8 tập 2: Luyện tập – Phương trình tích

Giải bài luyện tập Phương trình tích: Bài 23 ,24, 25, 26 trang 17 SGK Toán 8 tập 2 – Chương 3 Đại số.

Các em bài trước Dethikiemtra.com đã giải tại đây: Phương trình tích (Bài 21,22 trang 17 SGK Toán 8 tập 2:)

Bài 23. Giải các phương trình:

a) x(2x – 9) = 3x(x – 5)
⇔ 2×2 – 9x = 3×2 – 15x
⇔ 2×2 – 9x – 3×2 + 15x = 0
⇔ -x2 + 6x = 0
⇔ -x(x – 6) = 0
⇔ -x = 0 hoặc x – 6 = 0
–x = 0 ⇔ x = 0
x – 6 = 0 ⇔x = 6
Phương trình có tập nghiệm S = {0; 6}

b) 0,5x(x – 3) = (x -3)(1,5x – 1)
⇔ 0,5x(x – 3) – (x – 3)(1,5x – 1) = 0
⇔ (x – 3)(0,5x – 1,5x + 1) = 0
⇔ (x – 3)(- x + 1) = 0
⇔ x – 3 = 0 hoặc – x + 1 = 0
x – 3 = 0 ⇔ x = 3
– x + 1 = 0 ⇔x = 1
Phương trình có tập nghiệm S = {1; 3}

c) 3x – 15 = 2x(x – 5)
⇔ 3(x – 5) – 2x(x – 5) = 0
⇔ (x – 5)(3 – 2x) = 0
⇔ x – 5 = 0 hoặc 3 – 2x = 0

(1) x – 5 = 0 ⇔ x = 5

(2) 3 – 2x = 0 ⇔ x = 3/2

Phương trình có tập nghiệm S = {5; 3/2}

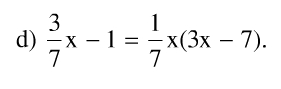
⇔ 3x – 7 = x(3x – 7)
⇔ x(3x – 7) – (3x – 7) = 0
⇔ (3x – 7)(x – 1) = 0
⇔ 3x – 7= 0 hoặc x – 1 = 0

(1) 3x – 7 = 0 ⇔ x = 7/3

(2) x – 1 = 0 ⇔ x = 1

Phương trình có tập nghiệm S = {7/3 ; 1 }

Bài 24 trang 17. Giải các phương trình:

a) (x² – 2x + 1) – 4 = 0

b) x² – x = -2x + 2

c) 4x² + 4x + 1 = x²

d) x² – 5x + 6 = 0

Advertisements (Quảng cáo)

Hướng dẫn giải:

a) (x² – 2x + 1) – 4 = 0
⇔ (x – 1)² – 2² = 0
⇔ (x – 1 + 2)(x – 1 – 2) = 0
⇔(x + 1)(x – 3) = 0
⇔ x + 1 = 0 hoặc x – 3 = 0
x + 1 = 0 ⇔ x = – 1
x – 3 = 0 ⇔ x = 3
Phương trình có tập nghiệm S = {-1; 3}

b) x² – x = -2x + 2

⇔ x² – x + 2x – 2 = 0

⇔ x(x – 1) + 2(x – 1) =0

⇔ (x – 1) (x + 2) = 0

⇔ x – 1 = 0 hoặc x + 2 = 0

⇔ x = 1 hoặc x = -2

Tập nghiệm của phương trình là: S = {1; -2}

c) 4x² + 4x + 1 = x²

⇔ 4x² + 4x + 1 – x² = 0

⇔ (2x + 1)² – x² = 0

Advertisements (Quảng cáo)

⇔ (2x + 1 + x) (2x + 1 – x) = 0

⇔ (3x + 1) (x + 1 ) = 0

⇔ x = -1/3 hoặc x = -1

Tập nghiệm của phương trình là: S = {-1/3; -1}

d) x² – 5x + 6 = 0
⇔ x² – 2x – 3x + 6 = 0
⇔ x(x – 2) – 3(x – 2) = 0
⇔ (x – 2)(x – 3) = 0
⇔ x – 2 = 0 hoặc x – 3 = 0
x – 2 = 0 ⇔ x = 2
x – 3 = 0 ⇔ x = 3
Phương trình có tập nghiệm S = {2; 3}

Bài 25 trang 17. Giải các phương trình:

a) 2x³ + 6x² = x²+ 3x

b) (3x – 1)(x² + 2) = (3x – 1)(7x – 10)

Đáp án:

a) 2x³ + 6x² = x² + 3x
⇔ 2x³ + 6x² – x² – 3x = 0
⇔ 2x²(x + 3) – x(x + 3) = 0
⇔ x(x + 3)(2x – 1) = 0
⇔ x = 0 hoặc x + 3 = 0 hoặc 2x – 1 = 0

⇔ x = 0 hoặc x = -3 hoặc x = 1/2

PT có tập nghiệm S = {0; -3 ; 1/2}

b) (3x – 1)(x² + 2) = (3x – 1)(7x – 10)
⇔ (3x – 1)(x² + 2) – (3x – 1)(7x – 10) = 0
⇔ (3x -1)(x² + 2 – 7x + 10) = 0
⇔ (3x – 1)(x² – 7x + 12) = 0
⇔ (3x – 1)(x – 3)(x – 4) = 0
⇔ 3x – 1 = 0 hoặc x – 3 = 0 hoặc x – 4 = 0

⇔ x = 1/3 hoặc x = 3 hoặc x = 4

PT có tập nghiệm S = {1/3 ; 3 ; 4 }

Bài 26 Toán 8. Trò chơi: Giải toán nhanh
( Mỗi nhóm lần lượt giải các phương trình trong phiếu học tập theo bàn. Nhóm nào giải nhanh và đúng là Nhóm thắng cuộc)
Đề số 1: Giải phương trình: 2(x-2) + 1 = x -1
Đề số 2 : Thế giá trị x vừa tìm được vào tìm y trong phương trình sau:
(x + 3) y = x+ y
Đề số 3: Thế giá trị y vừa tìm được vào tìm z trong phương trình sau:
Đề số 4: Thế giá trị z vừa tìm được vào tìm t trong phương trình sau:
Đáp án và hướng dẫn giải bài 26: