Kiểm tra học kì 2 Toán 6: Tính số học sinh giỏi của khối 6 đó

Bài 1: ( 2 điểm ) Tính hợp lí (nếu có thể):

a) \(12\dfrac{5}{{17}} – 5\dfrac{2}{{17}}\)

b)   \(\dfrac{{ – 5}}{{12}}.\dfrac{2}{{11}} + \dfrac{{ – 5}}{{12}}.\dfrac{9}{{11}} + \dfrac{5}{{12}}\)

c) \(6\dfrac{9}{{10}} + \left( {\dfrac{2}{5} – \dfrac{1}{{10}}} \right)\)

d) \(\dfrac{5}{{2.4}} + \dfrac{5}{{4.6}} + \dfrac{5}{{6.8}} + … + \dfrac{5}{{48.50}}\)

Bài 2 :( 2 điểm ) Tìm x, biết :

a)    \(1\dfrac{1}{4}.x =  – 1\dfrac{7}{8}\)

b)  \(\dfrac{3}{4} + \dfrac{1}{4}:x =  – 2\)

c) \({x^2}:\dfrac{{16}}{{11}} = \dfrac{{11}}{4}\)

d) \(\left| {x – 2} \right| – 3 = 0\) 

Bài 3 :( 3 điểm )

Một  khối 6 có 270 học sinh bao gồm ba loại : Giỏi, Khá và Trung bình. Số học sinh trung bình chiếm \(\dfrac{7}{{15}}\) số học sinh cả khối, số học sinh khá bằng  \(\dfrac{5}{8}\)  số học sinh còn lại.

a) Tính số học sinh giỏi của khối 6 đó

b) Tính tỉ số phần trăm của số học sinh giỏi so với học sinh cả khối 6 đó

Bài 4: (3đ) Trên cùng một nửa mặt phẳng bờ chứa tia Ox, vẽ hai tia Oy, Oz sao cho  \(\widehat {xOz} = {42^o};\widehat {xOy} = {84^o}\)

a) Tia Oz có là tia phân giác của \(\widehat {xOy}\)   không? Tại sao?

b) Vẽ tia Oz’ là tia đối của tia Oz. Tính số đo của \(\widehat {yOz’}\)

c) Gọi Om là tia phân giác của  \(\widehat {xOz}\) . Tính số đo của \(widehat {mOy},\,\widehat {mOz’}\)

Bài 1:

a) \(12\dfrac{5}{{17}} – 5\dfrac{2}{{17}}\)

\( = 12 – {\rm{ }}5 + \dfrac{5}{{17}} – \dfrac{2}{{17}}=7\dfrac{3}{{17}}\)

b) \(\dfrac{{ – 5}}{{12}}.\dfrac{2}{{11}} + \dfrac{{ – 5}}{{12}}.\dfrac{9}{{11}} + \dfrac{5}{{12}}\)

\(=\dfrac{{ – 5}}{{12}}.(\dfrac{2}{{11}} + \dfrac{9}{{11}}) + \dfrac{5}{{12}}\)

\(= \dfrac{{ – 5}}{{12}} + \dfrac{5}{{12}} = 0\)

c) \(6\dfrac{9}{{10}} + \left( {\dfrac{2}{5} – \dfrac{1}{{10}}} \right)\)

\(=6\dfrac{9}{{10}} – \dfrac{1}{{10}} + \dfrac{2}{5} = 6\dfrac{8}{{10}} + \dfrac{2}{5}\)

\( = 6\dfrac{4}{5} + \dfrac{2}{5} = 6 + \dfrac{6}{5} = 7\dfrac{1}{5}\)

d) \(\dfrac{5}{{2.4}} + \dfrac{5}{{4.6}} + \dfrac{5}{{6.8}} + … + \dfrac{5}{{48.50}}\)

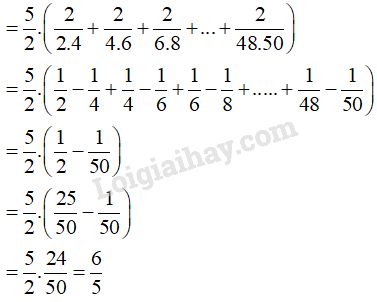
Bài 2:

a) \(1\dfrac{1}{4}.x =  – 1\dfrac{7}{8}\)

\(\eqalign{
& x = {5 \over 4}:( – {{15} \over 8}) \cr
& x = {5 \over 4}.{{ – 8} \over {15}} = – {2 \over 3} \cr} \)

b) \(\dfrac{3}{4} + \dfrac{1}{4}:x =  – 2\)

\(\dfrac{1}{4}:x =  – 2 – \dfrac{3}{4} =  – \dfrac{{11}}{4}\)

\(x = \dfrac{1}{4}:\dfrac{{ – 11}}{4} \)

\( x= \dfrac{1}{4}.\dfrac{{ – 4}}{{11}} =  – \dfrac{1}{{11}}\)

c) \({x^2}:\dfrac{{16}}{{11}} = \dfrac{{11}}{4}\)

\(\eqalign{
& {x^2} = {{11} \over 4}.{{16} \over {11}} = 4 \cr
& x = \pm 2 \cr} \)

d) \(\left| {x – 2} \right| – 3 = 0\)

\(\left| {x – 2} \right| = 3\)

TH1: \(x-2=3\Rightarrow  x = 5\)

TH2: \(x-1 =-3 \Rightarrow x= -2\)

Bài 3:

a) Số học sinh trung bình  là :\(\dfrac{7}{{15}}.270 = 126\) ( em)

Số học sinh còn lại  là :270 – 126 =144 ( em)

Số học sinh  khá  là \(\dfrac{5}{8}.144 = 90\) ( em)

Số học sinh giỏi  là 270 – (126 + 90) = 54 ( em)

b) Tỉ số phần trăm của số học sinh giỏi so với học sinh cả khối 6:

    54:270.100% = 20%

Bài 4:

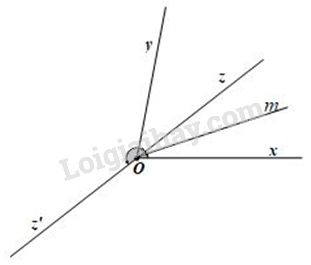
a) Trên cùng nửa mặt phẳng bờ chứa tia Ox vì \(\widehat {xOz} < \widehat {xOy}\)

 (42⁰ < 84⁰) nên tia Oz nằm giữa 2 tia Ox và Oy.

Vì tia Oz nằm giữa hai tia Ox và Oy nên

\(\widehat {xOz} + \widehat {zOy} = \widehat {xOy}\) hay \({42^o} + \widehat {zOy} = {80^o}\)

\( \Rightarrow \widehat {zOy} = {84^o} – {42^o} = {42^o}\)

Vậy \(\widehat {xOz} = \widehat {yOz} = {42^o}\)

Vì tia Oz nằm giữa hai tia Ox và Oy  và \(\widehat {xOz} = \widehat {yOz} = {42^o}\) nên Oz là tia phân giác của  \(\widehat {xOy}\)

b) Vì \(\widehat {yOz’}\) và \(\widehat {yOz}\) là hai góc kề bù nên:

\(\begin{array}{l}\widehat {yOz’} + \widehat {yOz} = {180^o}\\ \Rightarrow \widehat {yOz’} = {180^o} – \widehat {yOz}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = {180^o} – {42^o} = {138^o}\end{array}\)

Vì Om là tia phân giác của \(\widehat {xOz}\)  nên \(\widehat {xOm} = \widehat {mOz} = \dfrac{1}{2}\widehat {xOz} = \dfrac{1}{2}{.42^o} = {21^o}\)

Trên cùng nửa mặt phẳng bờ chứa tia Ox vì  \(\widehat {xOm} < \widehat {xOy}\)  (21⁰ < 84⁰) nên tia Om nằm giữa 2 tia Ox và Oy do đó:

\[\begin{array}{l}\widehat {mOx} + \widehat {mOy} = \widehat {xOy}\\\widehat {mOy} = \widehat {xOy} – \widehat {mOx}\\\,\,\,\,\,\,\,\,\,\,\,\,\, = {84^o} – {21^o} = {63^o}\end{array}\]

Vì tia Oz và Oz’ là 2 tia đối nhau nên \(\widehat {mOz}\)  và  \(\widehat {mOz’}\)  kề bù:

\(\begin{array}{l}\widehat {mOz’} + \widehat {mOz} = {180^o}\\\widehat {mOz’} = {180^o} – {21^o} = {159^o}\end{array}\)