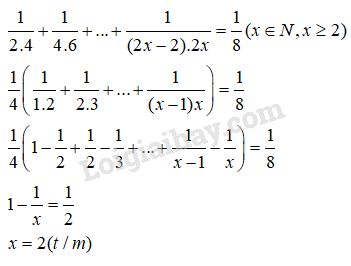Bài 1: (3,0đ). Thực hiện phép tính (Tính hợp lý nếu có thể)
\(a)\dfrac{{ – 10}}{{13}} + \dfrac{5}{{17}} – \dfrac{3}{{13}} + \dfrac{{12}}{{17}} – \dfrac{{11}}{{20}}\)
\(b)\dfrac{3}{4} + \dfrac{{ – 5}}{6} – \dfrac{{11}}{{ – 12}}\)
\(c)\;\,\left( {\,13\dfrac{4}{9} + 2\dfrac{1}{9}} \right)\, – 3\dfrac{4}{9}\)
\(d)1,25:\dfrac{{15}}{{20}} + \left( {25\% – \dfrac{5}{6}} \right):4\dfrac{2}{3}\)
Bài 2: (2,0đ). Tìm x , biết:
\({\text{a}})x – \dfrac{1}{3} = \dfrac{5}{{14}}.\dfrac{{ – 7}}{6}\)
\(b)\;\dfrac{3}{4} + \dfrac{1}{4}.x = 0,2\)
\(c)\,\,\dfrac{1}{{12}}{x^2} = 1\dfrac{1}{3}\)
Bài 3: (2,0đ). Lớp 6A có 45 học sinh. Trong giờ sinh hoạt lớp, để chuẩn bị cho buổi dã ngoại tổng kết năm học, cô giáo chủ nhiệm đã khảo sát địa điểm dã ngoại em yêu thích với ba khu du lịch sinh thái: Đầm Long, Khoang Xanh, Đảo Ngọc Xanh . Kết quả thu được như sau: \(\dfrac{1}{3}\) số học sinh cả lớp lựa chọn đi Đầm Long, số học sinh lựa chọn đi Khoang Xanh bằng \(\dfrac{2}{3}\) số học sinh còn lại.
a) Địa điểm nào được các bạn học sinh lớp 6A lựa chọn đi đông nhất?
b) Tính tỉ số phần trăm của số học sinh chọn đi Đảo Ngọc Xanh so với học sinh cả lớp.
Bài 4: (2,5đ).
Trên cùng một nửa mặt phẳng bờ chứa tia Oa, vẽ hai tia Ob và Oc sao cho \(\widehat {aOb} = {60^o};\widehat {aOc} = {120^o}\)
a) Tính số đo \(\widehat {bOc}\)
b) Chứng tỏ rằng: Ob là tia phân giác của \(\widehat {aOc}\)
c) Vẽ tia Ot là tia đối của tia Oa, tia Om là tia phân giác của \(\widehat {cOt}\) .
Chứng tỏ rằng : \(\widehat {bOc}\) và \(\widehat {cOm}\) là hai góc phụ nhau.
Bài 5: (0,5đ). Tìm x, biết:
\(\dfrac{1}{{2.4}} + \dfrac{1}{{4.6}} + … + \dfrac{1}{{(2x – 2).2x}} = \dfrac{1}{8}\) \((x \in N,x \ge 2)\)
Advertisements (Quảng cáo)

Bài 1:
\(a)\dfrac{{ – 10}}{{13}} + \dfrac{5}{{17}} – \dfrac{3}{{13}} + \dfrac{{12}}{{17}} – \dfrac{{11}}{{20}}\)
\( = \left( {\dfrac{{ – 10}}{{13}} – \dfrac{3}{{13}}} \right) + \left( {\dfrac{5}{{17}} + \dfrac{{12}}{{17}}} \right) \)\(\;- \dfrac{{11}}{{20}}\)
\( = ( – 1) + 1 – \dfrac{{11}}{{20}}\)
\( = – \dfrac{{11}}{{20}}\)
\(b)\dfrac{3}{4} + \dfrac{{ – 5}}{6} – \dfrac{{11}}{{ – 12}}\)
\( = \dfrac{{9 + ( – 10) + 11}}{{12}}\)
\( = \dfrac{{10}}{{12}}\)
\(= \dfrac{5}{6}\)
\(c)\;\,\left( {\,13\dfrac{4}{9} + 2\dfrac{1}{9}} \right)\, – 3\dfrac{4}{9}\)
\( = \,\left( {\,13\dfrac{4}{9} – 3\dfrac{4}{9}} \right) + 2\dfrac{1}{9}\)
\( = \,10 + 2\dfrac{1}{9}\)
Advertisements (Quảng cáo)
\( = \,12\dfrac{1}{9}\)
\(d)1,25:\dfrac{{15}}{{20}} + \left( {25\% – \dfrac{5}{6}} \right):4\dfrac{2}{3}\)
\( = \dfrac{5}{4}.\dfrac{4}{3} + \left( {\dfrac{1}{4} – \dfrac{5}{6}} \right).\dfrac{3}{{14}}\)
\( = \dfrac{5}{3} + \dfrac{7}{{12}}.\dfrac{3}{{14}}\)
\( = \dfrac{5}{3} + \dfrac{{ – 1}}{8} = \dfrac{{37}}{{24}}\)
Bài 2:
\({\text{a}})x – \dfrac{1}{3} = \dfrac{5}{{14}}.\dfrac{{ – 7}}{6}\)
\(x – \dfrac{1}{3} = \dfrac{{ – 5}}{{12}}\)
\(x = \dfrac{{ – 5}}{{12}} + \dfrac{1}{3}\)
\(x = \dfrac{{ – 1}}{{12}}\)
\(b)\;\dfrac{3}{4} + \dfrac{1}{4}.x = 0,2\)
\(\dfrac{1}{4}.x = \dfrac{1}{5} – \dfrac{3}{4}\)
\(\dfrac{1}{4}x = \dfrac{{ – 11}}{{20}}\)
\(x = \dfrac{{ – 11}}{5}\)
\(\eqalign{ & c)\,\,{1 \over {12}}{x^2} = 1{1 \over 3} \cr& \,\,\,\,\,{x^2} = {4 \over 3}:{1 \over {12}} \cr& \,\,\,\,\,\,{x^2} = {4 \over 3}.{{12} \over 1} = 16 \cr & \,\,\,\,\,\,\,x = \pm 4 \cr} \)
Bài 3:
a) Số học sinh chọn đi Đầm Long: \(45.\dfrac{1}{3} = 15(hs)\)
Số học sinh chọn đi Khoang Xanh: \((45 – 15).\dfrac{2}{3} = 20(hs)\)
Số học sinh chọn đi Đảo Ngọc Xanh: \(45 – (15 + 20) = 10(hs)\)
Số học sinh chọn đi Khoang Xanh là nhiều nhất
b) Tỉ số phần trăm số học sinh chọn đi Đảo Ngọc Xanh so với học sinh cả lớp : \(\dfrac{{10.100}}{{45}}\% = 22,22\% \)
Bài 4:
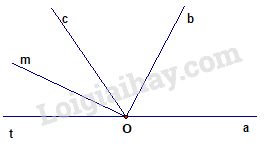
a) Vì tia Ob, Oc cùng một nửa mặt phẳng bờ chứa tia Oa, và \(\widehat {aOb} < \widehat {aOc}\left( {{{60}^o} < {{120}^o}} \right)\) nên tia Ob nằm giữa hai tia Oa và Oc.Ta có:\(\widehat {bOc} = \widehat {aOc} – \widehat {aOb} = {120^o} – {60^o} = {60^0}\)
b) Ob là tia phân giác của \(\widehat {aOc}\) vì:
+) Ob nằm giữa tia Oa và Oc+) \(\widehat {aOb} = \widehat {bOc} = \dfrac{{\widehat {aOc}}}{2}( = {60^0}\)c) Vẽ tia Ot là tia đối của tia Oa và Om là tia phân giác của \(\widehat {cOt}\). Chứng tỏ: \(\widehat {bOc}\) và \(\widehat {cOm}\) phụ nhau.
Vì tia Ot là tia đối của tia Oa \( \Rightarrow \widehat {cOt} = {60^0}\)Tia Om là tia phân giác của \(\widehat {cOt}\) \( \Rightarrow \widehat {cOm} = {30^0}\)\(\widehat {bOc} + \widehat {cOm} = {90^0}\)\(\widehat {bOc};\widehat {cOm}\) là hai góc phụ nhau
Bài 5: