
PHẦN I: TRẮC NGHIỆM KHÁCH QUAN (5.0 điểm)
Khoanh tròn chữ cái in hoa trước câu trả lời đúng:
1.: Trong các phân số \(\dfrac{{ – 11}}{{12}};\dfrac{{ – 20}}{{23}};\dfrac{{ – 27}}{{360}};\dfrac{{ – 5}}{{ – 7}}\) phân số lớn nhất là:
A. \(\dfrac{{ – 11}}{{12}}\); B. \(\dfrac{{ – 20}}{{23}}\);
C. \(\dfrac{{ – 27}}{{360}}\); D. \(\dfrac{{ – 5}}{{ – 7}}\)
2. Các cặp phân số bằng nhau là:
A . \(\dfrac{{ – 3}}{4}\) và \(\dfrac{{ – 4}}{3}\) B . \(\dfrac{{ – 2}}{3}\) và \(\dfrac{6}{9}\)
C . \(\dfrac{3}{7}\)\(\dfrac{3}{7}\) và \(\dfrac{{ – 3}}{7}\) D .  \(\dfrac{7}{8}\) và \(\dfrac{{ – 35}}{{ – 40}}\)
\(\dfrac{7}{8}\) và \(\dfrac{{ – 35}}{{ – 40}}\)
3.Tích \((3).\dfrac{5}{9}\) bằng :
A. \(\dfrac{5}{{27}}\) B. \(\dfrac{{ – 15}}{{27}}\)
C. \(\dfrac{{15}}{9}\) D. \(\dfrac{{ – 5}}{3}\)
4. Kết quả rút gọn phân số \(\dfrac{{ – 210}}{{300}}\) đến tối giản là:
A . \(\dfrac{{ – 21}}{{30}}\) B . \(\dfrac{{21}}{{30}}\)
C . \(\dfrac{{ – 7}}{{10}}\) D . \(\dfrac{7}{{10}}\)
5. So sánh hai phân số \(\dfrac{{ – 3}}{4}\) và \(\dfrac{4}{{ – 5}}\)
A. \(\dfrac{{ – 3}}{4} = \dfrac{4}{{ – 5}}\) B. \(\dfrac{{ – 3}}{4} < \dfrac{4}{{ – 5}}\)
C. \(\dfrac{{ – 3}}{4} > \dfrac{4}{{ – 5}}\) D. \(\dfrac{{ – 3}}{4} \ge \dfrac{4}{{ – 5}}\)
6. Kết quả của phép tính \(\dfrac{1}{4} + \dfrac{3}{4}\left( {\dfrac{2}{3} – \dfrac{1}{2}} \right)\) bằng:
A. \(\dfrac{1}{6}\) B. \(\dfrac{1}{4}\)
C. \(\dfrac{3}{8}\) D. \(\dfrac{3}{4}\)
7. Số đối của \(\dfrac{5}{{11}}\) là:
A. \(\dfrac{5}{{11}}\) B. \(\dfrac{{ – 5}}{{11}}\)
C. \(\dfrac{{ – 11}}{5}\) D. \(\dfrac{{11}}{5}\)
8. Số nghịch đảo của \(\dfrac{{ – 8}}{9}\) là:
A. \(\dfrac{9}{8}\) B. \(\dfrac{8}{9}\)
C. \(\dfrac{{ – 8}}{9}\) D. \(\dfrac{9}{{ – 8}}\)
9. Kết quả của phép tính \(\dfrac{3}{5}.\dfrac{{ – 15}}{9}\) là:
A. \( – 1\) B. \(1\)
C. \(\dfrac{{ – 5}}{3}\) D. \(\dfrac{{ – 5}}{3}\)
1.0: Phân số \(\dfrac{{ – 16}}{{11}}\) được viết dưới dạng hỗn số là :
A. \(1\dfrac{{ – 5}}{{11}}\) B. \(1\dfrac{5}{{11}}\)
Advertisements (Quảng cáo)
C. \( – 1\dfrac{5}{{11}}\) D . \( – 1\dfrac{{( – 5)}}{{11}}\)
1.1: Phân số \(\dfrac{2}{5}\) viết dưới dạng phần trăm là:
A. \(\dfrac{{13}}{3}\) B. \(2,5\% \)
C. \(4\% \) D. \(40\% \)
1.2: Lớp 6A có 40 học sinh trong đó có 12,5\% là học sinh giỏi. Số học sinh giỏi của lớp 6A là:
A. \(5\) B. \(6\)
C. \(8\) D. \(10\)
1.3: An có  viên bi, An cho Bình \(\dfrac{2}{5}\) số bi của mình , số viên bi Bình được An cho là :
viên bi, An cho Bình \(\dfrac{2}{5}\) số bi của mình , số viên bi Bình được An cho là :
A. \(4\) B. \(8\)
C. \(10\) D. \(6\)
1.4: \(\dfrac{3}{7}\) của \(28\) thì bằng \(\dfrac{{12}}{7}\) của số:
A. \(7\) B. \(12\)
C. \(4\) D.\(\dfrac{{36}}{{49}}\)
1.5. Cho biểu thức \(M = \dfrac{{ – 5}}{{n – 2}}\). Điều kiện để biểu thức \(M\) là phân số là:
A. \(n = 2\) B. \(n \ne 2\)
C. \(n \ne 1\) D. \(n \ne – 1\)
1.6: Góc vuông là góc có số đo:
A. Bằng \({180^0}\). B. Nhỏ hơn \({90^0}\)
C. Bằng \({90^0}\) D. Lớn hơn \({90^0}\)
1.7: Góc \({30^0}\) phụ với góc có số đo bằng:
Advertisements (Quảng cáo)
A. \({0^0}\) B. \({60^0}\)
C. \({90^0}\) D. \({180^0}\)
1.8: Biết rằng \(\widehat {MNP} = {180^0}\) câu nào sau đây không đúng
A.Ba điểm \(M,N,P\) thẳng hàng B.Hai tia \(MP\) và \(MN\) đối nhau
C. Hai tia \(NP\) và \(NM\) đối nhau D. Góc \(MNP\) là góc bẹt
1.9: Nếu \(\widehat {xOy} + \widehat {yOz} = \widehat {xOz}\) thì:
A. Tia \(Oz\) nằm giữa hai tia \(Ox\) và \(Oy\).
B. Tia \(Ox\) nằm giữa hai tia \(Oz\) và \(Oy\)
C. Tia \(Oy\) nằm giữa hai tia \(Ox\) và \(Oz\)
D. Không có tia nào nằm giữa hai tia còn lại
2.0: Hình gồm các điểm cách đều điểm \(I\) một khoảng cách \(IA = 3cm\) là:
A. tia \(IA\)
B. đường tròn tâm \(I\) bán kính \(3cm\)
C. đoạn thẳng \(IA\)
D. cả A; B; C đều đúng
B/ TỰ LUẬN ( 5,0đ)
Bài 1: (1,0đ):
a) Thực hiện phép tính: \( – 4\dfrac{3}{5} + 1\dfrac{3}{5}\)
b) Tìm \(x\), biết: \(2x – 3 = 7\)
Bài 2: ( 1,5 điểm) Lớp 6A có \(48\) học sinh, số học sinh giỏi chiếm \(\dfrac{1}{6}\) số học sinh cả lớp. Số học sinh trung bình bằng \(300/%\) số học sinh giỏi, còn lại là học sinh khá. Tính số học sinh của mỗi loại .
Bài 3: (2,0đ) Trên cùng một nửa mặt phẳng có bờ chứa tia \(Ox\), vẽ 2 tia \(Ot\) và \(Oy\) sao cho \(\widehat {xOt} = {35^0};\widehat {xOy} = {70^0}\).
a) Hỏi tia nào nằm giữa 2 tia còn lại ? Vì sao ?
b) Tính \(\widehat {tOy}\) ?
c) Hỏi tia \(Ot\) có là phân giác của góc \(\widehat {xOy}\) không? Vì sao?
Bài 4: (0,5đ) Tìm các giá trị của \(n \in Z\) để \(n + 13\) chia hết cho \(n – 2\).

A/ Trắc nghiệm
| 1 | 2 | 3 | 4 | 5 |
| D | D | D | C | C |
| 6 | 7 | 8 | 9 | 10 |
| C | B | D | A | C |
| 11 | 12 | 13 | 14 | 15 |
| D | A | B | A | B |
| 16 | 17 | 18 | 19 | 20 |
| C | B | B | C | B |
B/ Tự luận
Bài 1:
a) \( – 4\dfrac{3}{5} + 1\dfrac{3}{5} = \dfrac{{ – 23}}{5} + \dfrac{8}{5}\)\(\, = \dfrac{{ – 15}}{5} = – 3\)
\(\eqalign{ & b)\,\,2x – 3 = 7 \cr & \,\,\,\,2x = 7 + 3 \cr & \,\,\,\,2x = 10 \cr & \,\,\,\,\,\,x = 10:2 \cr & \,\,\,\,\,\,x = 5 \cr} \)
Bài 2:
Số học sinh giỏi là: \(48.\dfrac{1}{6} = 8\)
Số học sinh trung bình là: \(8.300\% = 24\)
Số học sinh khá là: \(48 – (8 + 24) = 16\)
Bài 3:
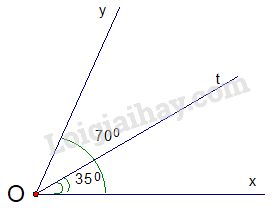
a) Vì hai tia Oy, Ot cùng nằm trên một nửa mặt phẳng có bờ chứa tia \(Ox\) và \(\widehat {xOt} < \widehat {xOy}\), \(({35^0} < {70^0})\) nên tia \(Ot\) nằm giữa 2 tia \(Ox\), \(Oy\)
b) Vì tia Ot nằm giữa hai tia Ox và Oy nên ta có:
\(\eqalign{& \widehat {xOt} + \widehat {tOy} = \widehat {xOy} \cr & \Rightarrow \widehat {tOy} = \widehat {xOy} – \widehat {xOt} \cr & \Rightarrow \widehat {tOy} = {70^o} – {35^o} \cr & \Rightarrow \widehat {tOy} = {35^o} \cr} \)
c) Tia \(Ot\) là phân giác của \(\widehat {xOy}\) vì:
+) Ot nằm giữa hai tia Ox và Oy
+) \(\widehat {xOt} = \widehat {tOy} = {35^o}\)
Bài 4:
Ta có: \(\dfrac{{n + 13}}{{n – 2}} = 1 + \dfrac{{15}}{{n – 2}}\)
Để \(n + 13 \vdots n – 2\) thì \(n – 2 \in U(15)\)
\(\Rightarrow n – 2 \in {\rm{\{ }} \pm 1; \pm 3; \pm 5; \pm 15\} \)
\(\Rightarrow n = \pm 1; \pm 3;5;7; – 13;17\).

![[[THCS Thanh Vân] thi kì 2 lớp 8 môn Văn: Viết đoạn văn (12 – 15 câu) trình bày cảm nhận của em về khổ thơ trên trong đó có sử dụng 1 câu phủ định 1 câu cảm thán.](https://dethikiemtra.com/wp-content/uploads/2020/09/unnamed-100x75.jpg)





