1.Trên mặt phẳng tọa độ, tập hợp các điểm biểu diễn số phức z thỏa mãn điều kiện \(\left| {z – (3 + 2i)} \right| = 2\) là:
A. Đường tròn tâm I(3;2), bán kính R = 2.
B. Đường tròn tâm I(-3;2), bán kính R = 2.
C. Đường tròn tâm I(3;2), bán kính \(R = \sqrt 2 .\)
D. Đường tròn tâm I(3;-2), bán kính R – 2.
2. Cho \({\rm{w}} = \dfrac{{{z^2} – {{\left( {\overline z } \right)}^2}}}{{1 + z.\overline z }}\)với z là số phức tùy ý cho trước. Mệnh đề nào dưới đây đúng?
A. w là số ảo. B. w = -1.
C. w = 1. D. w là số thực.
3. Gọi \({z_1},{z_2},{z_3},{z_4}\) là các nghiệm phức của phương trình \({({z^2} + z)^2} + 4({z^2} + z) – 12 = 0.\) Tính \(S = {\left| {{z_1}} \right|^2} + {\left| {{z_2}} \right|^2} + {\left| {{z_3}} \right|^2} + {\left| {{z_4}} \right|^2}.\)
A. S = 18. B. S = 16.
C. S = 17. D. S = 15.
4. Trong không gian với hệ tọa độ Oxyz, cho đường thẳng \(d:\left\{ \begin{array}{l}x = 1 – t\\y = 3\\z = – 1 + 2t\end{array} \right.,\) vectơ nào dưới đây là một vectơ chỉ phương của đường thẳng d?
A.\(\overrightarrow {{u_4}} = ( – 1;3;2).\)
B.\(\overrightarrow {{u_1}} = (1;0; – 2).\)
C.\(\overrightarrow {{u_2}} = (1;3; – 1).\)
D.\(\overrightarrow {{u_3}} = (1;0;2).\)
5. Cho số phức z = 3 + 4i, \((a,b \in \mathbb{R}).\) Mệnh đề nào dưới đây là sai?
A.z là số thực.
B.\(\overline z = 3 – 4i.\)
C. Phần ảo của số phức z bằng 4.
D.\(\left| z \right| = 5.\)
6. Trong không gian với hệ tọa độ Oxyz, cho điểm A(3;-2;-2), B(3;2;0). Phương trình mặt cầu đường kính AB là:
A.\({(x – 3)^2} + {y^2} + {(z + 1)^2} = 20.\)
B.\({(x – 3)^2} + {y^2} + {(z + 1)^2} = 5.\)
C.\({(x + 3)^2} + {y^2} + {(z – 1)^2} = 5.\)
D.\({(x + 3)^2} + {y^2} + {(z – 1)^2} = 20.\)
7. Cửa lớn của một trung tâm giải trí có dạng Parabol (như hình vẽ). Người ta dự định lắp cửa kính cường lực 12 ly với đơn giá 800.000 đồng/\({m^2}.\) Tính chi phú để lắp cửa.
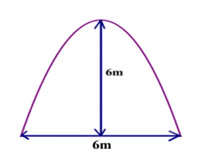
A. 9.600.000 đồng. B. 19.200.000 đồng.
C. 33.600.000 đồng. D. 7.200.000 đồng.
8. Trong không gian với hệ tọa độ Oxyz, cho điểm A(2;-1;1) và hai mặt phẳng (P): 2x – z + 1 = 0; (Q): y – 2 = 0. Viết phương trình mặt phẳng \((\alpha )\) đi qua A và vuông góc với hai mặt phẳng (P), (Q).
A.\((\alpha ):2x – y + z – 4 = 0.\)
B.\((\alpha ):x + 2z – 4 = 0.\)
C.\((\alpha ):2x + y – 4 = 0.\)
D.\((\alpha ):x + y + z = 0.\)
9. Trong không gian với hệ tọa độ Oxyz, cho ba điểm A(0;0;1), B(-1;-2;0), C(2;0;-1). Tập hợp các điểm M cách đều ba điểm A, B, C là đường thẳng \(\Delta .\) Viết phương trình \(\Delta .\)
A.\(\Delta :\left\{ \begin{array}{l}x = \dfrac{1}{3} + t\\y = \dfrac{2}{3} + t\\z = t\end{array} \right.\)
B.\(\Delta :\left\{ \begin{array}{l}x = \dfrac{1}{3} + t\\y = – \dfrac{2}{3} – t\\z = t\end{array} \right.\)
C.\(\Delta :\left\{ \begin{array}{l}x = 1 + t\\y = – \dfrac{3}{2} + t\\z = t\end{array} \right.\)
D.\(\Delta :\left\{ \begin{array}{l}x = \dfrac{1}{2} + t\\y = – 1 – t\\z = – \dfrac{1}{2} + t\end{array} \right.\)
1.0: Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P): \(\dfrac{x}{2} + \dfrac{y}{1} + \dfrac{z}{3} = 1,\) vectơ nào dưới đây là một vectơ pháp tuyến của mặt phẳng (P)?
A.\(\overrightarrow {{n_1}} = (3;6;2).\)
B.\(\overrightarrow {{n_3}} = ( – 3;6;2).\)
C.\(\overrightarrow {{n_2}} = (3;6;2).\)
D. \(\overrightarrow {{n_4}} = ( – 3;6; – 2).\)
1.1: Trong không gian với hệ tọa độ Oxyz, viết phương trình mặt phẳng \((\alpha )\) chứa trục Ox và đi qua điểm M(2;-1;3).
A.\((\alpha ): – y + 3z = 0.\)
B.\((\alpha ):2x – z + 1 = 0.\)
C.\((\alpha ):x + 2y + z – 3 = 0.\)
D.\((\alpha ):3y + z = 0.\)
1.2: Hàm số f(x) nào dưới đây thỏa mãn \(\int {f(x)dx = \ln \left| {x + 3} \right|} + C?\)
A.\(f(x) = (x + 3)\ln (x + 3) – x.\)
B.\(f(x) = \dfrac{1}{{x + 3}}.\)
C.\(f(x) = \dfrac{1}{{x + 2}}.\)
D.\(f(x) = \ln (ln(x + 3)).\)
1.3: Cho hình phẳng (H) giới hạn bởi đường cong \({y^2} – y + x = 0\) và đường thẳng x + y – 2 = 0. Tính diện tích S của hình (H).
A. S = 6. B. S = 14.
C.\(S = \dfrac{{17}}{6}.\) D.\(S = \dfrac{1}{6}.\)
1.4: Cho số phức z = a + bi \((a,b \in \mathbb{R})\) thỏa mãn \((1 + i)z – \dfrac{{3 + 4i}}{{2 – i}} = {(1 – i)^2}.\) Tính P = 10a + 10b.
A. P = – 42. B. P = 20.
Advertisements (Quảng cáo)
C. P = 4. D. P = 2.
1.5: Tìm phần thực a của số phức \(z = {i^2} + … + {i^{2019}}.\)
A. a = 1. B.\(a = – {2^{1009}}.\)
C.\(a = {2^{1009}}.\) D. a = -1.
1.6: Trong không gian với hệ tọa độ Oxyz, cho hai đường thẳng \({d_1}:\left\{ \begin{array}{l}x = 1 + t\\y = 0\\z = – 5 + t\end{array} \right.\) và \({d_2}:\left\{ \begin{array}{l}x = 0\\y = 4 – 2t’\\z = 5 + 3t’\end{array} \right..\) Viết phương trình đường thẳng vuông góc chung \(\Delta \) của \({d_1}\) và \({d_2}.\)
A.\(\Delta :\dfrac{x}{2} = \dfrac{{y – 4}}{{ – 3}} = \dfrac{{z – 5}}{{ – 2}}.\)
B.\(\Delta :\dfrac{{x – 4}}{2} = \dfrac{y}{{ – 3}} = \dfrac{{z – 2}}{2}.\)
C.\(\Delta :\dfrac{{x – 1}}{{ – 2}} = \dfrac{y}{3} = \dfrac{{z + 5}}{2}.\)
D.\(\Delta :\dfrac{{x – 4}}{{ – 2}} = \dfrac{y}{3} = \dfrac{{z + 2}}{2}.\)
1.7: Trong không gian với hệ tọa độ Oxyz, cho điểm A(-3;5;-5), B(5;-3;7) và mặt phẳng (P): x + y + z = 0. Tìm tọa độ của điểm M trên mặt phẳng (P) sao cho \(M{A^2} – 2M{B^2}\) đạt giá trị lớn nhất.
A. M(-2;1;1). B. M(2;-1;1).
C. M(6;-18;12). D. M(-6;18;12).
1.8: Trong không gian với hệ tọa độ Oxyz, cho hai điểm M(3;0;0), N(2;2;2). Mặt phẳng (P) thay đổi qua M, N cắt các trục Oy, Oz lần lượt tại B(0;b;0), C(0;0;c), \((b \ne 0,c \ne 0).\) Hệ thức nào dưới đây là đúng?
A. b + c = 6. B. bc = 3(b+c).
C. bc = b + c. D.\(\dfrac{1}{b} + \dfrac{1}{c} = \dfrac{1}{6}.\)
1.9: Cho \(I = \int\limits_{\dfrac{\pi }{4}}^{\dfrac{\pi }{2}} {\dfrac{{{{\cot }^3}x}}{{{{\sin }^2}x}}dx} \) và u = cotx. Mệnh đề nào dưới đây là đúng?
A.\(I = \int\limits_{\dfrac{\pi }{4}}^{\dfrac{\pi }{2}} {{u^3}du.} \) B.\(I = \int\limits_0^1 {{u^3}du.} \)
C.\(I = – \int\limits_0^1 {{u^3}du.} \) D.\(I = \int\limits_0^1 {udu.} \)
2.0: Giả sử hàm số y = f(x) có đạo hàm liên tục trên \(\left[ {0;2} \right]\) biết \(\int\limits_0^2 {f(x)dx = 8.} \) Tính \(\int\limits_0^2 {\left[ {f(2 – x) + 1} \right]} dx.\)
A. – 9. B. 9.
C. 10. D. – 6.
2.1: Tìm các số thực x, y thỏa mãn (1 – 3i)x – 2y + (1 + 2y)i = 3 – 6i.
A. x = – 5, y = – 4. B. x = 5, y = 4.
C. x = 5, y = – 4. D. x = – 5, y = 4.
2.2: Gọi \({z_1},{z_2}\) là hai nghiệm phức của phương trình \({z^2} + bz + c = 0,(c \ne 0).\) Tính \(P = \dfrac{1}{{z_1^2}} + \dfrac{1}{{z_2^2}}\) theo b,c.
A.\(P = \dfrac{{{b^2} – 2c}}{c}.\)
B.\(P = \dfrac{{{b^2} + 2c}}{{{c^2}}}.\)
C.\(P = \dfrac{{{b^2} + 2c}}{c}.\)
D.\(P = \dfrac{{{b^2} – 2c}}{{{c^2}}}.\)
2.3: Tìm các giá trị thực của tham số m để số phức \(z = {m^3} + 3{m^2} – 4 + (m – 1)i\) là số thuần ảo.
A.\(\left[ \begin{array}{l}m = 1\\m = – 2\end{array} \right..\) B. m = 1.
C. m = -2. D. m = 0.
2.4: Trong mặt phẳng tọa độ, tập hợp điểm M(x;y) biểu diễn số phức z = x + yi \((x,y \in \mathbb{R})\) thỏa mãn \(\left| {z – 1 + 3i} \right| = \left| {z – 2 – i} \right|\) là:
A. Đường tròn đường kính AB với A(1;-3), B(2;1).
B. Đường thẳng trung trực của đoạn thẳng AB với A(1;-3), B(2;1).
C. Trung điểm của đoạn thẳng AB với A(1;-3), B(2;1).
D. Đường thẳng trung trực của đoạn thẳng AB với A(-1;3), B(-2;-1).
2.5: Trong không gian với hệ tọa độ Oxyz, cho mặt cầu \((S)\): \({(x + 3)^2} + {y^2} + {(z – 2)^2} = {m^2} + 4.\) Tìm tất cả các giá trị thực của tham số m để mặt cầu (S) tiếp xúc với mặt phẳng (Oyz).
A. m = 0. B. m = 2, m = -2.
Advertisements (Quảng cáo)
C.\(m = \sqrt {5.} \) D.\(m = \sqrt 5 ,m = – \sqrt 5 .\)
2.6: Cho \(\int\limits_0^{\dfrac{\pi }{2}} {{{\cos }^2}} 2xdx = \dfrac{\pi }{a} + \dfrac{b}{c},\) với a, b, c là số nguyên dương \(\dfrac{b}{c}\) tối giản. Tính P = a + b + c.
A. P = 15. B. P = 23.
C. P = 24. D. P = 25.
2.7: Cho \(\int\limits_0^1 {\dfrac{{dx}}{{\sqrt {2x + a} }}} ,\) với a > 0. Tìm a nguyên đề \(I \ge 1.\)
A. a = 1.
B. a = 0.
C. Vô số giá trị của a.
D. Không có giá trị nào của a.
2.8: Trong không gian với hệ tọa độ Oxyz, tìm tọa độ điểm \(A’\) đối xứng với A(-1;0;3) qua mặt phẳng (P): x + 3y – 2z – 7 = 0.
A.\(A’\) (-1;-6;1). B.\(A’\)(0;3;1).
C.\(A’\)(1;6;-1). D.\(A’\)(11;0;-5).
2.9: Tìm nguyên hàm của hàm số \(f(x) = {3^x}.\)
A.\(\int {f(x)dx = \dfrac{{{3^x}}}{{\ln 3}}} + C.\)
B.\(\int {f(x)dx = \dfrac{{{3^{x + 1}}}}{{x + 1}}} + C.\)
C.\(\int {f(x)dx = {3^x}} + C.\)
D.\(\int {f(x)dx = {3^x}} .3\ln 3 + C.\)
Câu 30: Số phức z = 4 – 3i có điểm biểu diễn là:
A. M(4;3). B. M(3;4).
C. M(4;-3). D. M(-3;4).
3.1: Tính \(I = \int\limits_{ – 1}^1 {\dfrac{{{x^3}}}{{{x^2} + 2}}} dx.\)
A. I = 1. B. I = 0.
C. I = 3. D. I = -3.
3.2: Trong không gian với hệ tọa độ Oxyz, cho đường thẳng \(\Delta :\dfrac{{x – 3}}{2} = \dfrac{{y – 2}}{1} = \dfrac{z}{1}\) và mặt phẳng \((\alpha ):3x + 4y + 5z + 8 = 0.\) Góc giữa đường thẳng \(\Delta \) và mặt phẳng \((\alpha )\) có số đo là:
A.\({45^ \circ }.\) B.\({90^ \circ }.\)
C.\({30^ \circ }.\) D.\({60^ \circ }.\)
3.3: Trong không gian với hệ tọa độ Oxyz, phương trình nào dưới đây là phương trình của mặt cầu?
A.\({x^2} + {y^2} + {z^2} + 2x – 4y + 10 = 0.\)
B.\({x^2} + {y^2} + {z^2} + 2x – 2y – 2z – 2 = 0.\)
C.\({x^2} + 2{y^2} + {z^2} + 2x – 2y – 2z – 2 = 0\)
D.\({x^2} – {y^2} + {z^2} + 2x – 2y – 2z – 2 = 0.\)
3.4: Trong không gian với hệ tọa độ Oxyz, cho vật thể nằm giữa hai mặt phẳng x = 0 và x = 3. Biết rằng thiết diện của vật thể cắt bởi mặt phẳng vuông góc với trục Ox tại điểm có hoành độ \(x(0 \le x \le 3)\) là một hình vuông cạnh là \(\sqrt {9 – {x^2}} .\) Tính thể tích V của vật thể.
A. V = 171. B.\(V = 171\pi .\)
C.\(V = 18.\) D.\(V = 18\pi .\)
3.5: Tìm số phức z thỏa mãn \(z + 2\overline z = 2 – 4i.\)
A.\(z = \dfrac{2}{3} – 4i.\)
B.\(z = – \dfrac{2}{3} + 4i.\)
C.\(z = \dfrac{2}{3} + 4i.\)
D.\(z = – \dfrac{2}{3} – 4i.\)
3.6: Biết \(\int {\dfrac{{{{(x – 1)}^{2016}}}}{{(x + 2)^{{2018}}{{}}}}} dx = \dfrac{1}{a}{\left( {\dfrac{{x – 1}}{{x + 2}}} \right)^b} + C,\)\(\;x \ne 2,\) với a, b nguyên dương. Mệnh đề nào dưới đây đúng?
A. a < b. B. a = b.
C. a = 3b. D. b – a = 4034.
3.7: Trong không gian với hệ tọa độ Oxyz, cho \(\overrightarrow u = 2\overrightarrow i – 3\overrightarrow j – \overrightarrow k ,\) tọa độ của \(\overrightarrow u \) là:
A.\(\overrightarrow u = (2;3; – 1).\)
B.\(\overrightarrow u = (2; – 1; – 3).\)
C.\(\overrightarrow u = (2;3;1).\)
D.\(\overrightarrow u = (2; – 3; – 1).\)
3.8: Trong không gian với hệ tọa độ Oxyz, cho đường thẳng \(d:\left\{ \begin{array}{l}x = t\\y = 1 – t\\z = – 1 + 2t\end{array} \right.\)và mặt phẳng \((\alpha ):x + 3y + z – 2 = 0.\) Khẳng định nào dưới đây là đúng?
A. Đường thẳng d cắt mặt phẳng \((\alpha ).\)
B. Đường thẳng d nằm trên mặt phẳng \((\alpha ).\)
C. Đường thẳng d vuông góc với mặt phẳng \((\alpha ).\)
D. Đường thẳng d song song với mặt phẳng\((\alpha ).\)
3.9: Cho hàm số \(F(x) = ({x^2}{\rm{ + ax + b)}}{{\rm{e}}^x},\) \(f(x) = ({x^2} + 3x + 4){e^x}.\) Biết a, b là các số thực đề F(x) là một nguyên hàm của hàm f(x). Tính S = a + b.
A. S = – 6. B. S = 12.
C. S = 6. D. S = 4.
4.0: Cho hàm số f(x) xác đinh trên \((e; + \infty )\) thỏa mãn \(f'(x) = \dfrac{1}{{x.\ln x}}\) và \(f({e^2}) = 0.\) Tính \(f({e^4}).\)
A.\(f({e^4}) = ln2.\) B.\(f({e^4}) = – ln2.\)
C.\(f({e^4}) = 3ln2.\) D.\(f({e^4}) = 2.\)
4.1: Cho hình phẳng (H) (phần gạch chéo trong hình vẽ). Tính thể tích V của khối tròn xoay tạo thành khi quay (H) quanh trục hoành.
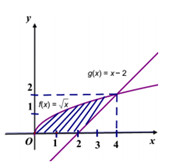
A.\(V = 8\pi .\) B.\(V = 10\pi .\)
C.\(V = \dfrac{{8\pi }}{3}.\) D.\(V = \dfrac{{16\pi }}{3}.\)
4.2: Cho đồ thị hàm số y = f(x). Diện tích S của hình phẳng (phần tô đen trong hình vẽ) được tính theo công thức nà dưới đây?
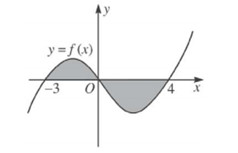
A.\(S = \int\limits_{ – 3}^0 {f(x)dx} – \int\limits_0^4 {f(x)dx} .\)
B.\(S = \int\limits_{ – 3}^4 {f(x)dx} .\)
C.\(S = – \int\limits_{ – 3}^0 {f(x)dx} + \int\limits_0^4 {f(x)dx} .\)
D.\(S = \int\limits_{ – 3}^1 {f(x)dx} + \int\limits_1^4 {f(x)dx} .\)
4.3: Tìm số thực m > 1 thỏa mãn \(\int\limits_1^m {x(2\ln x + 1)dx = 2{m^2}} .\)
A. m = e. B.m = 2.
C. m = 0. D.\(m = {e^2}.\)
4.4: Tập hợp các điểm biểu diễn của số phức z trên mặt phẳng tạo độ là đường tròn tâm I(0;1), bán kính R = 3. Mệnh đề nào dưới đây là đúng?
A.\(\left| {z – 1} \right| = 3.\)
B.\(\left| {z – i} \right| = 3.\)
C.\(\left| {z – i} \right| = \sqrt 3 .\)
D.\(\left| {z + i} \right| = 3.\)
4.5: Phương trình nào dưới đây nhận hai số phức \( – \sqrt 3 i\) và \(\sqrt 3 i\) là nghiệm ?
A.\({z^2} + 5 = 0.\) B. \({z^2} + 3 = 0.\)
C.\({z^2} + 9 = 0.\) D.\({z^2} + \sqrt 3 = 0.\)
4.6: Cho hai số phức \({z_1},{z_2}\) thỏa mãn \(\left| {{z_1} – 1 + i} \right| = 1\) và \({z_2} = 2i{z_1}.\) Tìm giá trị nhỏ nhất \({P_{\min }}\) của biểu thức \(P = \left| {2{z_1} – {z_2}} \right|.\)
A.\({P_{\min }} = 2 – \sqrt 2 .\)
B.\({P_{\min }} = 8 – \sqrt 2 .\)
C.\({P_{\min }} = 2 – 2\sqrt 2 .\)
D.\({P_{\min }} = 4 – 2\sqrt 2 .\)
4.7: Trong không gian với hệ tọa độ Oxyz, cho hai điểm A(3;2;1), M(3;0;0) và mặt phẳng (P): x + y + z – 3 = 0. Đường thẳng \(\Delta \) đi qua điểm M, nằm trong mặt phẳng (P) so cho khoảng cách từ điểm A đến đường thẳng \(\Delta \) là nhỏ nhất. Gọi vectơ \(\overrightarrow u = (a;b;c)\) là một vectơ chỉ phương của \(\Delta \) (a, b, c là các số nguyên có ước chung lớn nhất là 1). Tính P = a + b + c.
A. – 1. B. 1.
C. 2. D. 0.
4.8: Cho hai số phức \({z_1},{z_2}\) thỏa mãn \(\left| {{z_1}} \right| = \sqrt 2 ,\left| {{z_2}} \right| = 2.\) Gọi M, N lần lượt là các điểm biểu diễn của số phức \({z_1}\) và \({z_2}\). Biết góc tạo bởi hai vectơ \(\overrightarrow {OM} ,\overrightarrow {ON} \) bằng \({45^ \circ }.\) Tính giá trị của biểu thức \(P = \left| {\dfrac{{{z_1} + {z_2}}}{{{z_1} – {z_2}}}} \right|.\)
A.\(P = \sqrt 5 .\) B.\(P = \dfrac{1}{{\sqrt 5 }}.\)
C.\(P = \dfrac{{2 + \sqrt 2 }}{{2 – \sqrt 2 }}.\) D.\(P = \dfrac{{\sqrt 2 + 2}}{{\sqrt 2 – 2}}.\)
4.9: Trong không gian với hệ tọa độ Oxyz, cho hai điểm M(1;0;2), N(1;-1;-1) và mặt phẳng (P): 2x + 2y – z + 2 = 0. Một mặt cầu đi qua M, N tiếp xúc với mặt phẳng (P) tại điểm E. Biết E luôn thuộc một đường tròn cố định, tính bán kính của đường tròn đó.
A.\(R = \dfrac{{\sqrt {10} }}{2}.\) B.\(R = \sqrt {10.} \)
C.\(R = 10.\) D.\(R = 2\sqrt 5 .\)
5.0: Cho hàm số f(x) có đạo hàm liên tục \(\mathbb{R}\) và thỏa mãn f(x) > 0, \(\forall x \in \mathbb{R}.\) Biết f(0) = 1 và \(f'(x) = (6x – 3{x^2}).f(x).\) Tìm tất cả các giá trị thực của tham số m để phương trình f(x) = m có nghiệm duy nhất.
A.\(\left[ \begin{array}{l}m > {e^4}\\0 < m < 1\end{array} \right..\) B.\(1 < m < {e^4}.\)
C.\(\left[ \begin{array}{l}m > {e^4}\\m < 1\end{array} \right..\) D.\(1 \le m \le {e^4}.\)

|
1 |
2 |
3 |
4 |
5 |
|
A |
A |
C |
B |
A |
|
6 |
7 |
8 |
9 |
10 |
|
B |
B |
B |
D |
A |
|
11 |
12 |
13 |
14 |
15 |
|
D |
B |
D |
D |
D |
|
16 |
17 |
18 |
19 |
20 |
|
D |
C |
D |
B |
C |
|
21 |
22 |
23 |
24 |
25 |
|
B |
D |
A |
B |
D |
|
26 |
27 |
28 |
29 |
30 |
|
D |
D |
C |
A |
C |
|
31 |
32 |
33 |
34 |
35 |
|
B |
D |
B |
C |
C |
|
36 |
37 |
38 |
39 |
40 |
|
C |
D |
B |
D |
A |
|
41 |
42 |
43 |
44 |
45 |
|
D |
A |
D |
B |
B |
|
46 |
47 |
48 |
49 |
50 |
|
D |
D |
A |
D |
A |

![[Cao Bằng] Đề kiểm tra học kì 2 lớp 12 môn Văn năm 2015](https://dethikiemtra.com/wp-content/uploads/2015/06/thpt-nguyen-binh-cao-bang-100x75.jpg)