
1. Trong các mệnh đề sau, mệnh đề nào đúng?
A. Tồn tại một hình đa diện có số cạnh bằng số đỉnh
B. Tồn tại một hình đa diện có số cạnh và mặt bằng nhau.
C. Số đỉnh và số mặt của một hình đa diện luôn bằng nhau
2. Mệnh đề nào sau đây là mệnh đề đúng?
Số các cạnh của một hình đa diện luôn:
A. Lớn hơn \(6\)
B. Lớn hơn \(7\)
C. Lớn hơn hoặc bằng \(7\)
D. Lớn hơn hoặc bằng \(6\)
3. Trong các mệnh đề sau, mệnh đề nào sai?
A.Khối lăng trụ tam giác là khối đa diện.
B.Khối hộp là khối đa diện.
C. Lắp ghép 2 khối đa diện luôn được khối đa diện lồi.
D.Khối tứ diện là khối đa diện lồi.
4. Chọn khẳng định sai.
A. Mỗi cạnh của khối đa diện là cạnh chung của đúng \(2\) mặt của khối đa diện.
B. Hai mặt bất kì của khối đa diện luôn có ít nhất một điểm chung.
C. Mỗi đỉnh của khối đa diện là đỉnh chung của ít nhất \(3\) mặt.
D. Mỗi mặt của khối đa diện có ít nhất ba cạnh.
5. Phép đối xứng qua mặt phẳng biến một điểm thuộc mặt phẳng đó thành:
A. không tồn tại ảnh của điểm đó qua phép đối xứng
B. một điểm nằm ngoài mặt phẳng
C. một điểm bất kì thuộc mặt phẳng
D. một điểm trùng với nó.
6. Phép dời hình biến đoạn thẳng thành:
A. đoạn thẳng dài bằng nó
B. đoạn thẳng vuông góc với nó
C. đoạn thẳng song song với nó
D. đoạn thẳng dài gấp đôi nó
7. Phép dời hình biến đường thẳng thành:
A. đường tròn B. một điểm
C. đoạn thẳng D. đường thẳng
8. Trong các kí hiệu sau, kí hiệu nào không phải của khối đa diện đều?
A. \(\left\{ {3;3} \right\}\) B. \(\left\{ {4;3} \right\}\)
C. \(\left\{ {5;3} \right\}\) D. \(\left\{ {4;4} \right\}\)
9. Khối đa diện đều có 20 mặt thì có bao nhiêu cạnh?
A. 24 B. 12
C. 30 D. 60
10: Cho hình chóp tứ giác đều \(S.ABCD\) có chiều cao h, góc ở đỉnh của mặt bên bằng \({60^0}\). Thể tích hình chóp là:
A. \(\dfrac{{3{h^3}}}{2}\) B. \(\dfrac{{{h^3}}}{3}\)
C.\(\dfrac{{2{h^3}}}{3}\) D. \(\dfrac{{{h^3}\sqrt 3 }}{3}\)
11: Cho tứ diện \(ABCD\) có các cạnh \(AB,AC,AD\) đôi một vuông góc với nhau, \(AB = 6a,AC = 7a,AD = 4a\). Gọi \(M,N,P\) lần lượt là trung điểm của các cạnh \(BC,CD,DB\). Thể tích V của tứ diện \(AMNP\) là:
\(A.\,\,V = \dfrac{{7{a^3}}}{2}\) \(B.\,\,V = 14{a^3}\)
\(C.\,\,V = \dfrac{{28{a^3}}}{3}\) \(D.\,\,V = 7{a^3}\)
12: Thể tích khối hộp chữ nhật có diện tích đáy S và độ dài cạnh bên a là:
Advertisements (Quảng cáo)
\(A.\,\,V = S.a\) \(B.\,\,V = {S^2}a\)
\(C.\,\,V = \dfrac{1}{3}Sa\) \(D.\,\,V = \dfrac{{{S^2}}}{a}\)
13: Thể tích khối lập phương có cạnh 2a là:
\(A.\,\,{a^3}\) \(B.\,\,2{a^3}\)
\(C.\,\,\,6{a^3}\) \(D.\,\,\,8{a^3}\)
14: Cho hình lăng trụ \(ABC.A’B’C’\), \(\Delta ABC\) đều có cạnh bằng \(a,AA’ = a\)và đỉnh \(A’\) cách đều\(A,B,C\). Thể tích khối lăng trụ \(ABC.A’B’C’\) là:
\(A.\,\,\dfrac{{{a^3}\sqrt 2 }}{2}\) \(B.\,\,\dfrac{{{a^3}\sqrt 2 }}{4}\)
\(C.\,\,\dfrac{{{a^3}\sqrt 2 }}{8}\) \(D.\,\,\dfrac{{\sqrt 2 {a^3}}}{3}\)
15: Cho hình lăng trụ \(ABCD.A’B’C’D’\) có đáy \(ABCD\)là hình chữ nhật với \(AB = \sqrt 3 ,AD = \sqrt 7 \). Hai mặt bên \(\left( {ABB’A’} \right)\) và \(\left( {ADD’A’} \right)\) lần lượt tạo với đáy những góc \({45^0}\) và \({60^0}\). Tính thể tích khối hộp nếu biết cạnh bên bằng 1.
\(A.\,\,V = 3\) \(B.\,\,V = 2\)
\(C.\,\,V = 4\) \(D.\,\,V = 8\)

|
Câu |
1 |
2 |
3 |
4 |
5 |
|
Đáp án |
D |
D |
C |
B |
D |
|
Câu |
6 |
7 |
8 |
9 |
10 |
|
Đáp án |
A |
D |
D |
C |
C |
|
Câu |
11 |
12 |
13 |
14 |
15 |
|
Đáp án |
D |
A |
D |
B |
A |
1. Hình đa diện luôn có số đỉnh và số mặt nhỏ hơn số cạnh
Không phải hình đa diện nào cũng có số đỉnh bằng số mặt, ví dụ hình lập phương có 8 đỉnh và 6 mặt
Hình tứ diện có số đỉnh bằng số mặt (bằng 4).
Chọn D.
Chú ý khi giải:
Một số em sẽ chọn đáp án C khi lấy ví dụ tứ diện mà không chú ý đến trường hợp hình hộp.
2. Tứ diện là hình đa diện đơn giản nhất có cạnh bằng 6 nên số cạnh của hình đa diện luôn lớn hơn hoặc bằng 6.
Chọn D.
3. – Khối lăng trụ tam giác, khối hộplà các khối đa diện.
– Khối tứ diện là một khối đa diện lồi.
– Không phải khi nào lắp ghép 2 khối đa diện ta cũng được khối đa diện lồi.
Chọn C.
Chú ý khi giải:
Một số em sẽ nghĩ đáp án C là đúng nhưng thực chất khi lắp ghép hai khối đa diện ta chưa chắc đã nhận được khối đa diện lồi.
4. Các khẳng định A, C, D đúng
Chọn B.
5. Phép đối xứng qua mặt phẳng (P) là phép biến hình biến mỗi điểm thuộc (P) thành chính nó.
Chọn D.
6. Phép dời hình bảo toàn khoảng cách giữa 2 điểm nên đoạn thẳng sẽ có độ dài bằng đoạn thẳng đã cho.
Advertisements (Quảng cáo)
Chọn A.
7. Phép dời hình biến đường thẳng thành đường thẳng.
Chọn D.
Chú ý khi giải:
Một số em sẽ chọn đáp án C vì không đọc kỹ đáp án.
8. Có 5 khối đa diện, đó các loại \(\left\{ {3;3} \right\},\left\{ {4;3} \right\},\left\{ {3;4} \right\},\left\{ {5;3} \right\},\left\{ {3;5} \right\}\)
Vậy kí hiệu \(\left\{ {4;4} \right\}\) không phải kí hiệu của khối đa diện đều nào cả.
Chọn D.
9. Khối đa diện mười hai mặt đều thuộc loại \(\left\{ {3;5} \right\}\) nên mỗi mặt có 3 cạnh
Mỗi cạnh là cạnh chung của 2 mặt nên tổng số cạnh của đa diện là \(20.3:2 = 30\) (cạnh)
Chọn C.
Chú ý khi giải:
Một số em sẽ chọn nhầm đáp án D vì quên không chia cho 2 (mỗi cạnh lặp lại 2 lần).
10:
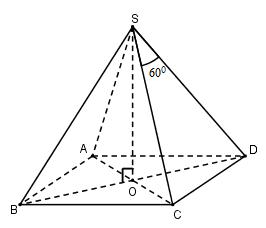
Gọi \(O = AC \cap BD\).
Vì chóp \(S.ABCD\) đều nên \(SO \bot \left( {ABCD} \right)\)
Đặt \(SA = SB = SC = SD = a\)
Tam giác \(SCD\) có:\(SC = SD;\widehat {CSD} = {60^0} \Rightarrow \Delta SCD\)đều\( \Rightarrow CD = SC = SD = a\)
\( \Rightarrow \) Hình vuông \(ABCD\) cạnh \(a \Rightarrow AC = BD = a\sqrt 2 \)\( \Rightarrow OC = \dfrac{1}{2}AC = \dfrac{{a\sqrt 2 }}{2}\)
\(SO \bot \left( {ABCD} \right) \Rightarrow SO \bot OC \Rightarrow \Delta SOC\) vuông tại O
\( \Rightarrow SO = \sqrt {S{C^2} – O{C^2}} \)
\(\Rightarrow h = \sqrt {{a^2} – \dfrac{{{a^2}}}{2}} = \dfrac{{a\sqrt 2 }}{2}\) \( \Rightarrow a = h\sqrt 2 \)
\( \Rightarrow {S_{ABCD}} = {a^2} = {\left( {h\sqrt 2 } \right)^2} = 2{h^2}\)
Vậy \({V_{S.ABCD}} = \dfrac{1}{3}SO.{S_{ABCD}} = \dfrac{1}{3}h.2{h^2} = \dfrac{{2{h^3}}}{3}\)
Chọn C.
11:
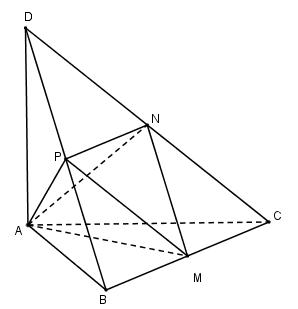
Ta có:
\(ABCD\) là tứ diện vuông tại \(A\) nên \({V_{ABCD}} = \dfrac{1}{6}AB.AC.AD = \dfrac{1}{6}.6a.7a.4a = 28{a^3}\).
Áp dụng công thức tính tỉ lệ thể tích các khối tứ diện ta có:
\(\dfrac{{{V_{DAPN}}}}{{{V_{DABC}}}} = \dfrac{{DA}}{{DA}}.\dfrac{{DP}}{{DB}}.\dfrac{{DN}}{{DC}} \)\(\,= \dfrac{1}{1}.\dfrac{1}{2}.\dfrac{1}{2} = \dfrac{1}{4}\)
\(\Rightarrow {V_{DAPN}} = \dfrac{1}{4}{V_{DABC}} = \dfrac{1}{4}.28{a^3} = 7{a^3}\)
\(\dfrac{{{V_{BAPM}}}}{{{V_{BADC}}}} = \dfrac{{BA}}{{BA}}.\dfrac{{BP}}{{BD}}.\dfrac{{BM}}{{BC}} \)\(\,= \dfrac{1}{1}.\dfrac{1}{2}.\dfrac{1}{2} = \dfrac{1}{4} \)
\(\Rightarrow {V_{BAPM}} = \dfrac{1}{4}{V_{BADC}} = \dfrac{1}{4}.28{a^3} = 7{a^3}\)
\(\dfrac{{{V_{CAMN}}}}{{{V_{CABD}}}} = \dfrac{{CA}}{{CA}}.\dfrac{{CM}}{{CB}}.\dfrac{{CN}}{{CD}} \)\(\,= \dfrac{1}{1}.\dfrac{1}{2}.\dfrac{1}{2} = \dfrac{1}{4}\)
\(\Rightarrow {V_{CAMN}} = \dfrac{1}{4}{V_{CABD}} = \dfrac{1}{4}.28{a^3} = 7{a^3}\)
Do đó \({V_{AMNP}} = {V_{ABCD}} – {V_{DAPN}} – {V_{BAPM}} – {V_{CAMN}} \)
\(= 28{a^3} – 7{a^3} – 7{a^3} – 7{a^3} = 7{a^3}\)
Chọn D.
12: Vì hình hộp chữ nhật cũng là hình lăng trụ nên thể tích của khối hộp cũng được tính bởi công thức \(V = Sh\), hay \(V = Sa\).
Chọn A.
13: Thể tích khối lập phương cạnh 2a là: \(V = {\left( {2a} \right)^3} = 8{a^3}\)
Chọn D.
Chú ý khi giải:
Một số em sẽ chọn nhầm đáp án A vì đọc không kĩ đề, một số em khác thì tính nhầm \({\left( {2a} \right)^3} = 6{a^3}\) và chọn C là sai.
14:
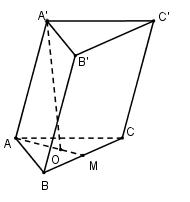
Gọi M là trung điểm của BC; O là tâm tam giác đều ABC
Vì A’ cách đều A, B, C nên \(A’O \bot \left( {ABC} \right) \Rightarrow A’O \bot AO \Rightarrow \Delta A’OA\) vuông tại O
Vì tam giác ABC đều cạnh a nên \(AM = \dfrac{{a\sqrt 3 }}{2} \Rightarrow AO = \dfrac{2}{3}AM = \dfrac{2}{3}.\dfrac{{a\sqrt 3 }}{2} = \dfrac{{a\sqrt 3 }}{3}\)
Xét tam giác vuông A’OA có: \(A’O = \sqrt {AA{‘^2} – A{O^2}} = \sqrt {{a^2} – \dfrac{{{a^2}}}{3}} = \dfrac{{a\sqrt 6 }}{3}\)
\({S_{ABC}} = \dfrac{{{a^2}\sqrt 3 }}{4}\)
Vậy \({V_{ABC.A’B’C’}} = A’O.{S_{ABC}} \)\(\,= \dfrac{{a\sqrt 6 }}{3}.\dfrac{{{a^2}\sqrt 3 }}{4} = \dfrac{{{a^3}\sqrt 2 }}{4}\)
Chọn B
15:
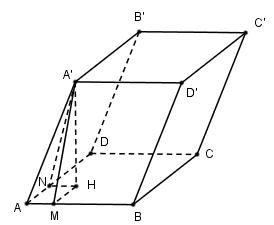
Kẻ \(A’H \bot \left( {ABCD} \right);HM \bot AB;HN \bot AD\)
Ta có: \(\left. \begin{array}{l}A’H \bot AB\\HM \bot AB\end{array} \right\} \Rightarrow AB \bot \left( {A’HM} \right) \)\(\Rightarrow AB \bot A’M\)
\(\left. \begin{array}{l}\left( {ABB’A’} \right) \cap \left( {ABCD} \right) = AB\\\left( {ABB’A’} \right) \supset A’M \bot AB\\\left( {ABCD} \right) \supset HM \bot AB\end{array} \right\} \\\Rightarrow \widehat {\left( {\left( {ABB’A’} \right);\left( {ABCD} \right)} \right)} = \widehat {\left( {A’M;HM} \right)} = \widehat {A’MH} = {45^o}\)
Chứng minh tương tự ta có \(\widehat {A’NH} = {60^0}\)
Đặt \(A’H = x\) khi đó ta có:
\(A’N = \dfrac{x}{{\sin 60}} = \dfrac{{2x}}{{\sqrt 3 }},\)
\(AN = \sqrt {AA{‘^2} – A'{N^2}} = \sqrt {1 – \dfrac{{4{x^2}}}{3}} = HM\)
Mà \(HM = x.\cot 45 = x\)
\( \Rightarrow x = \sqrt {1 – \dfrac{{4{x^2}}}{3}} \)
\(\Leftrightarrow {x^2} = 1 – \dfrac{{4{x^2}}}{3}\)
\(\Leftrightarrow \dfrac{{7{x^2}}}{3} = 1\)
\(\Rightarrow {x^2} = \dfrac{3}{7} \Rightarrow x = \sqrt {\dfrac{3}{7}} \)
\({S_{ABCD}} = \sqrt 3 .\sqrt 7 = \sqrt {21} \)
Vậy \({V_{ABCD.A’B’C’D’}} = A’H.{S_{ABCD}} \) \(= \sqrt {\dfrac{3}{7}} .\sqrt {21} = 3\)
Chọn A.






