Đề kiểm tra 45 phút Chương 1 – Khối đa diện Hình học 12: Số cạnh của một khối chóp tam giác là?

1. Số cạnh của một khối chóp tam giác là?

A. 4.                    B. 7.

C. 6.                    D. 5.

2. Khi tăng kích thước mỗi cạnh của khối hộp chữ nhật lên 5 lần thì thể tích khối hộp chữ nhật tăng bao nhiêu lần?

A. 125.                B. 25.

 C. 15.                 D. 5.

3. Cho hình chóp S.ABCD có đáy là hình vuông cạnh a và SA vuông góc với (ABC). Tính khoảng cách từ trọng tâm G của tam giác SAB đến (SAC)?

\(A.\,\,\,\dfrac{{a\sqrt 3 }}{6}\).         \(B.\,\,\dfrac{{a\sqrt 2 }}{6}\).

\(C.\,\,\,\dfrac{{a\sqrt 3 }}{2}\).         \(D.\,\,\,\dfrac{a \sqrt 2}{4}\)

4. Một chiếc xe ô tô có thùng đựng hàng hình hộp chữ nhật với kích thước 3 chiều lần lượt là 2m; 1,5m; 0,7m. Tính thể tích thùng đựng hàng của xe ôtô đó.

\(A.\,\,14{m^3}\).        \(B.\,\,4,2{m^3}\).

\(C.\,\,8{m^3}\).          \(D.\,\,2,1{m^3}\)

5. Cho khối lăng trụ tam giác đều \(ABC.{A_1}{B_1}{C_1}\) có tất cả các cạnh bằng a. Gọi M là trung điểm của \(AA_1\). Thể tích khối chóp \(M.BC{A_1}\) là:

\(A.\,\dfrac{{{a^3}\sqrt 3 }}{{12}}\)                     \(B.\,\dfrac{{{a^3}\sqrt 3 }}{{24}}\)

\(C.\,\dfrac{{{a^3}\sqrt 3 }}{6}\)                          \(C.\,\dfrac{{{a^3}\sqrt 3 }}{8}\)

6. Cho hình chóp tam giác S.ABC có đáy ABC là tam giác đều cạnh a, cạnh \(SA = SB = SC = \dfrac{{a\sqrt 6 }}{3}\). Tính thể tích V của khối chóp đã cho.

\(A.\,\,V = \dfrac{{{a^3}}}{{12}}\)       \(B.\,\,\,V = \dfrac{{{a^3}\sqrt 2 }}{{12}}\)

\(C.\,\,V = \dfrac{{{a^3}}}{2}\)       \(D.\,\,V = \dfrac{{{a^3}\sqrt 3 }}{6}\)

7. Công thức tính thể tích của khối lăng trụ có diện tích đáy B và chiều cao h

\(A.\,\,\,V = \dfrac{4}{3}Bh\)               \(B.\,\,\,V = \dfrac{1}{3}Bh.\)

\(C.\,\,\,V = \dfrac{1}{2}Bh.\)             \(D.\,\,\,V = Bh.\)

8. Trung điểm các cạnh của một tứ diện đều là

A. các đỉnh của một hình mười hai mặt đều.

B. các đỉnh của một hình bát diện đều.

C. các đỉnh của một hình hai mươi mặt đều.

D. các đỉnh của một hình tứ diện đều.

9. Cho lăng trụ tam giác ABC.A’B’C’ có thể tích là V, khi đó thể tích của khối chóp A’.ABC là

 \(A.\,\,\dfrac{V}{3}\)              \(B.\,\,\dfrac{V}{4}\)

\(C.\,\,\dfrac{V}{6}\)             \(D.\,\,\dfrac{V}{2}\)

10: Khối lập phương là khối đa diện đều loại

A. {5;3}.         B. {3;4}.

C. {4;3}.         D. {3;5}.

11: Công thức tính thể tích của khối chóp có diện tích đáy B và chiều cao h

\(A.\,\,\,V = \dfrac{1}{2}Bh.\)           \(B.\,\,\,V = Bh.\)

\(C.\,\,\,V = \dfrac{1}{3}Bh.\)          \(D.\,\,V = \dfrac{{\sqrt 3 }}{2}Bh.\)

12: Có bao nhiêu loại khối đa diện đều?

A. 20.           B. 3.

C. 12.           D. 5.

13: Cho khối chóp S.ABCD có đáy ABCD là hình vuông cạnh a, cạnh bên SA vuông góc với đáy và SA = a. Tính thể tích V của khối chóp đã cho.

 \(A.\,\,V = \dfrac{{{a^3}}}{6}\)      \(B.\,\,\,V = \dfrac{{{a^3}}}{3}\)

\(C.\,\,V = {a^3}\)       \(D.\,\,V = \dfrac{{{a^3}}}{9}\)

14: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh bằng a. SA vuông góc với đáy; góc tạo bởi SC và (SAB) là 30⁰ . Gọi E, F là trung điểm của BC và SD. Tính khoảng cách giữa hai đường thẳng chéo nhau DE và CF.

\(A.\,\,\dfrac{{3a\sqrt {13} }}{{13}}\)         \(B.\,\,\,\dfrac{{4a\sqrt {13} }}{{13}}\)

\(C.\,\,\,\dfrac{{a\sqrt {13} }}{{13}}\)           \(D.\,\,\dfrac{{2a\sqrt {13} }}{{13}}\)

15. Chọn khẳng định đúng trong các khẳng định sau:

A. Hình bát diện đều có 8 đình.

B. Hình bát diện đều có các mặt là bát giác đều.

C. Hình bát diện đều có các mặt là hình vuông.

D. Hình bát diện đều là đa diện đều loại {3; 4}.

16: Cho khối chóp có 20 cạnh. Số mặt của khối chóp đó bằng bao nhiêu?

A. 12                       B. 10

C. 13                       D. 11

17: Hình lập phương có bao nhiêu mặt phẳng đối xứng?

A.  8                          B. 7

C. 9                           D. 6

18. Thể tích khối bát diện đều có cạnh bằng a

\(\begin{array}{l}A.\,\dfrac{{{a^3}\sqrt 2 }}{3}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,B.\,\dfrac{{{a^3}\sqrt 2 }}{6}\\C.\,\dfrac{{{a^3}\sqrt 3 }}{4}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,D.\,\dfrac{{{a^3}\sqrt 3 }}{8}\end{array}\)

19. Khối đa diện đều loại {4; 3} có bao nhiêu đỉnh?

A. 10                        B. 6

 C. 8                         D. 4

20. Tính thể tích của khối lăng trụ tam giác đều có tất cả các cạnh bằng a

\(\begin{array}{l}A.\,\,\,\dfrac{{\sqrt 2 }}{4}{a^3}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,B.\,\,\,\dfrac{{\sqrt 2 }}{3}{a^3}\\C.\,\,\,\dfrac{{\sqrt 3 }}{2}{a^3}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,D.\,\,\,\dfrac{{\sqrt 3 }}{4}{a^3}\end{array}\)

1. Tứ diện có 6 cạnh.

Chọn C

2. \(\begin{array}{l}V = B.h = abh\\V’ = B’.h’ = 5a.5b.5h = 125abh = 125V\end{array}\)

Chọn A

3.

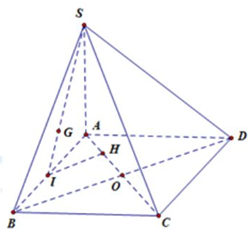
Gọi I là trung điểm của AB khi đó dựng \(IH \bot \left( {SAC} \right)\)

Khi đó \(IH = \dfrac{{OB}}{2} = \dfrac{{BD}}{4} = \dfrac{{a\sqrt 2 }}{4}\)

\(d\left( {G,\left( {SAC} \right)} \right) = \dfrac{2}{3}d\left( {I,\left( {SAC} \right)} \right)\)\(\, = \dfrac{2}{3}IH = \dfrac{{a\sqrt 2 }}{6}\)

Chọn B

4. Thể tích của thùng hàng đó là:

\(V = abc = 2.1,5.0,7 = 2,1\left( {{m^3}} \right)\)

Chọn D.

5.

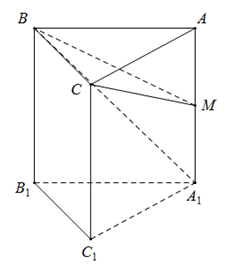
\(\Delta ABC\)là tam giác đều cạnh \(a\)nên có diện tích \({S_{ABC}} = \dfrac{{{a^2}\sqrt 3 }}{4}\)

Ta có \(AM = \dfrac{{A{A_1}}}{2} = \dfrac{a}{2}\)

Hai tứ diện \(MABC\)và \(M{A_1}BC\)có chung đỉnh\(C\), diện tích hai đáy \(MAB\)và \(M{A_1}B\)bằng nhau nên có thể tích bằng nhau, suy ra

\({V_{M.BC{A_1}}} = {V_{M.ABC}} = \dfrac{1}{3}AM.{S_{ABC}} \)\(\,= \dfrac{{{a^3}\sqrt 3 }}{{24}}\)

Chọn B.

6.

Gọi G là trọng tâm tam giác ABC, I là trung điểm của AB

\(\begin{array}{l}\left. \begin{array}{l}GA = GB = GC\\SA = SB = SC\end{array} \right\} \Rightarrow SG \bot \left( {ABC} \right)\\CG = \dfrac{2}{3}CI = \dfrac{2}{3}.\dfrac{{a\sqrt 3 }}{2} = \dfrac{{a\sqrt 3 }}{3}\\SG = \sqrt {S{C^2} – C{G^2}} \\ = \sqrt {{{\left( {\dfrac{{a\sqrt 6 }}{3}} \right)}^2} – {{\left( {\dfrac{{a\sqrt 3 }}{3}} \right)}^2}}  = \dfrac{{a\sqrt 3 }}{3}\\V = \dfrac{1}{3}SG.{S_{ABC}} \\\;\;\;\;= \dfrac{1}{3}.\dfrac{{a\sqrt 3 }}{3}.\dfrac{{{a^2}\sqrt 3 }}{4} = \dfrac{{{a^3}}}{{12}}\end{array}\)

Chọn A

7. Chọn D

8. Chọn B

9.

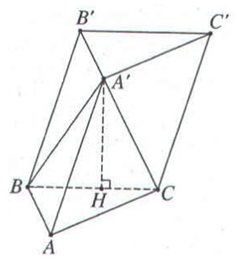
\(\begin{array}{l}{V_{ABC.A’B’C’}} = h.{S_{ABC}}\\{V_{A’.ABC}} = \dfrac{1}{3}h.{S_{ABC}}\\ \Rightarrow {V_{A’.ABC}} = \dfrac{V}{3}\end{array}\)

Chọn A.

10: Khối lập phương là khối đa diện đều loại {4,3}

Chọn C.

11: Chọn C

12: Có 5 khối đa diện đều.

Chọn D.

13:

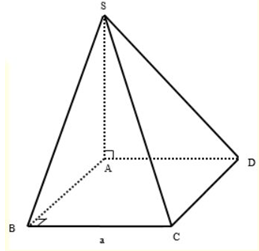
\(\begin{array}{l}{S_{ABCD}} = {a^2}\\{V_{S.ABCD}} = \dfrac{1}{3}SA.{S_{ABCD}}\\\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; = \dfrac{1}{3}a.{a^2} = \dfrac{{{a^3}}}{3}\end{array}\)

Chọn B

14:

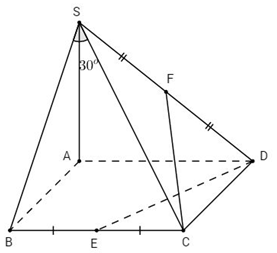
Góc giữa SC và (SAB) là góc BSC

\( \Rightarrow \widehat {BSC} = {30^o}\)

\(\begin{array}{l}SB = CB\cot {30^o} = a\sqrt 3 \\SA = \sqrt {S{B^2} – A{B^2}}  = \sqrt {3{a^2} – {a^2}}  = a\sqrt 2 \end{array}\)

Gắn hệ trục tọa độ như sau:

Gốc \(O \equiv A\left( {0;0;0} \right);\,Ox \equiv AB;\)

\(\,Oy \equiv AD;\,Oz \equiv AS\)

Tạo độ các điểm được xác định như sau:

\(\begin{array}{l}D\left( {0;a;0} \right);E\left( {a;\dfrac{a}{2};0} \right);C\left( {a;a;0} \right);F\left( {0;\dfrac{a}{2};\dfrac{a}{{\sqrt 2 }}} \right)\\\overrightarrow {DE} \left( {a; – \dfrac{a}{2};0} \right)\\\overrightarrow {CF} \left( { – a; – \dfrac{a}{2};\dfrac{a}{{\sqrt 2 }}} \right)\\\overrightarrow {DC} \left( {a;0;0} \right)\\\left[ {\overrightarrow {DE} ,\overrightarrow {CF} } \right] = \left( { – \dfrac{{{a^2}}}{{2\sqrt 2 }}, – \dfrac{{{a^2}}}{{\sqrt 2 }}; – {a^2}} \right)\\d = \dfrac{{\left| {\overrightarrow {DC} .\left[ {\overrightarrow {DE} ,\overrightarrow {CF} } \right]} \right|}}{{\left| {\left[ {\overrightarrow {DE} ,\overrightarrow {CF} } \right]} \right|}}\\\,\,\,\,\,\,\, = \dfrac{{\left| { – \dfrac{{{a^3}}}{{2\sqrt 2 }}} \right|}}{{\sqrt {{{\left( { – \dfrac{{{a^2}}}{{2\sqrt 2 }}} \right)}^2} + {{\left( { – \dfrac{{{a^2}}}{{\sqrt 2 }}} \right)}^2} + {{\left( { – {a^2}} \right)}^2}} }}\\\,\,\,\,\,\, = \dfrac{{a\sqrt {13} }}{{13}}\end{array}\)

Chọn C

15: Chọn D

16: Giả sử dáy của hình chóp có n cạnh \( \Rightarrow 2n = 20 \Leftrightarrow n = 10\)

Do đó số mặt của chóp là: 10 + 1 = 11

Chọn D.

17:

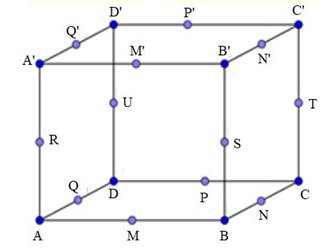
Xét khối lập phương ABCD.A’B’C’D’
Gọi M, N, P, Q lần lượt là trung điểm của AB, BC, CD, DA
M’, N’, P’, Q’ lần lượt là trung điểm của A’B’, B’C’, C’D’, D’A’
R, S, T, U lần lượt là trung điểm của AA’, BB’, CC’, DD’
Khối lập phương ABCD. A’B’C’D’ có 9 mp đối xứng như sau:
a) 3 mp đối xứng chia nó thành 2 khối hộp chữ nhật (là các mp MPP’M’, NQQ’N’, RSTU)
b) 6 mp đối xứng chia nó thành 2 khối lăng trụ tam giác (là các mp ACC’A’, BDD’B’, AB’C’D, A’BCD’, ABC’D’, A’B’CD)

Chọn C

18:

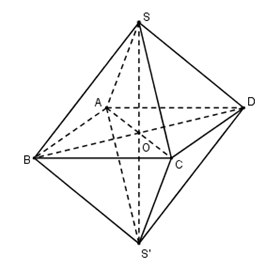
Thể tích khối bát diện đều \(V = 2{V_{S.ABCD}}\)

Gọi \(O = AC \cap BD \Rightarrow SO \bot \left( {ABCD} \right)\)

Vì ABCD là hình vuông nên \(AC = BD = a\sqrt 2 \)

\(\Rightarrow OA = \dfrac{1}{2}AC = \dfrac{{a\sqrt 2 }}{2}\)

\(SO \bot \left( {ABCD} \right) \Rightarrow SO \bot OA\)

\(\Rightarrow \Delta SOA\) vuông tại O

\( \Rightarrow SO = \sqrt {S{A^2} – O{A^2}}  = \sqrt {{a^2} – \dfrac{{{a^2}}}{2}} \)\(\, = \dfrac{{a\sqrt 2 }}{2}\)

\( \Rightarrow {V_{S.ABCD}} = \dfrac{1}{3}SO.{S_{ABCD}} \)

                      \(= \dfrac{1}{3}\dfrac{{a\sqrt 2 }}{2}.{a^2} = \dfrac{{{a^3}\sqrt 2 }}{6}\)

\( \Rightarrow V = 2\dfrac{{{a^3}\sqrt 2 }}{6} = \dfrac{{{a^3}\sqrt 2 }}{3}\)

Chọn A.

19: Lập phương loại {4;3} có M = 6 , Đ = 8

Chọn C.

20:

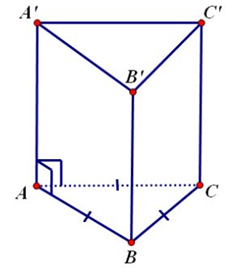
Thể tích khối lăng trụ tam giác đều có tất cả các cạnh a là:

\(V = \dfrac{{{a^2}\sqrt 3 }}{4}.a = \dfrac{{{a^3}\sqrt 3 }}{4}\)

Chọn D.