Trang Chủ Lớp 12 Bài tập SGK lớp 12

Bài tập 1,2,3,4 trang 9,10 SGK giải tích lớp 12 (Sự đồng biến, nghịch biến của hàm số )

Hướng dẫn giải và đáp án bài 1 trang 9; bài 2,3,4 trang 10 SGK giải tích lớp 12. Bài: Sự đồng biến, nghịch biến của hàm số – Chương 1.

Giải bài tập trong Sách giáo khoa:

Bài 1. Xét sự đồng biến, nghịch biến của các hàm số:

a) y = 4 + 3x – x² ; b) y = 1/3x³+ 3x² – 7x – 2 ;

c) y = x⁴– 2x² + 3 ; d) y = -x³ + x² – 5.

Đáp án bài 1: a) Tập xác định : D = R;

y’ = 3 – 2x => y’ = 0 ⇔ x = 3/2
Ta có Bảng biến thiên :

Hàmsố đồng biến trên khoảng (-∞; 3/2); nghịch biến trên khoảng ( 3/2; +∞ ).

b) Tập xác định D = R;
y’= x²+ 6x – 7 => y’ = 0 ⇔ x = 1, x = -7.

Bảng biến thiên :

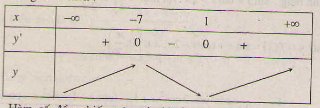
Hàmsố đồng biến trên các khoảng (-∞ ; -7), (1 ; +∞) ; nghịch biến trên các khoảng (-7 ; 1).

c) Tập xác định : D = R.

y’ = 4x³ – 4x = 4x(x²– 1) => y’ = 0 ⇔ x = -1, x = 0, x = 1.

Bảng biến thiên : (Học sinh tự vẽ)

Hàm số đồngbiến trên các khoảng (-1 ; 0), (1 ; +∞) ; nghịch biến trên các khoảng (-∞ ; -1), (0 ; 1).

d) Tập xác định : D = R. y’ = -3x²+ 2x => y’ = 0 ⇔ x = 0, x = 2/3.

Bảng biến thiên :

Advertisements (Quảng cáo)

Hàmsố đồng biến trên khoảng ( 0 ; 2/3) ; nghịch biến trên các khoảng (-∞ ; 0), ( 2/3; +∞).

Bài 2. Tìm các khoảng đơn điệu của các hàmsố:

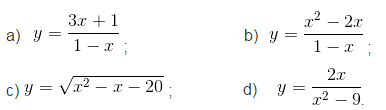
Đáp án bài 2: a) Tập xác định : D = R\{ 1 }

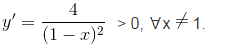
Hàm số đồng biến trên các khoảng : (-∞ ; 1), (1 ; +∞).

b) Tập xác định : D = R\{ 1 }.

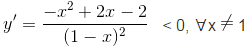
Hàmsố nghịch biến trên các khoảng : (-∞ ; 1), (1 ; +∞).

c) Tập xác định : D = (-∞ ; -4] ∪ [5 ; +∞).

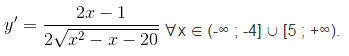
Advertisements (Quảng cáo)

Với x ∈ (-∞ ; -4) thì y’ < 0; với x ∈ (5 ; +∞) thì y’ > 0. Vậy hàm số nghịch biến trên khoảng (-∞ ; -4) và đồng biến trên khoảng (5 ; +∞).

d) Tập xác định : D = R\{ -3 ; 3 }.

Hàmsố nghịch biến trên các khoảng : (-∞ ; -3), (-3 ; 3), (3 ; +∞).

Bài 3. Chứng minh rằng hàmsố đồng biến trên khoảng (-1 ; 1) và nghịch biến trên các khoảng (-∞ ; -1) và (1 ; +∞).

Giải: Tập xác định : D = R.

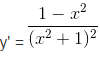
⇒ y’ = 0 ⇔ x=-1 hoặc x=1.

Bảng biến thiên :

Vậy hàm số đồng biến trên khoảng (-1 ; 1); nghịch biến trên các khoảng (-∞ ; -1), (1 ; +∞).

Bài 4. (trang 10 SGK Giải tích 12). Chứng minh rằng hàm số đồng biến trên khoảng (0 ; 1) và nghịch biến trên các khoảng (1 ; 2).

Giải: Tập xác định : D = [0 ; 2]; 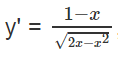, ∀x ∈ (0 ; 2); y’ = 0 ⇔ x = 1.

Bảng biến thiên :

Vậy hàm số đồng biến trên khoảng (0 ; 1) và nghịch biến trên khoảng (1 ; 2).

Bài 5. Chứng minh các bất đẳng thức sau:

a) tanx > x (0 < x < π/2);

b) tanx > x +x³/3 (0 < x <π/2 ).

Giải: a) Xét hàm số y = f(x) = tanx – x với x ∈ [0 ; π/2).

Ta có : y’ = 1/cos²x – 1 ≥ 0, x ∈ [0 ;π/2); y’ = 0 ⇔ x = 0. Vậy hàm số luôn đồng biến trên [0 ; π/2).

Từ đó ∀x ∈ (0 ; π/2) thì f(x) > f(0) ⇔ tanx – x > tan0 – 0 = 0 hay tanx > x.

b) Xét hàm số y = g(x) = tanx – x – x³/3. với x ∈ [0 ; π/2).

Ta có : y’ = 1/cos²x – 1 – x²= 1 + tan²x – 1 – x²= tan²x – x²

= (tanx – x)(tanx + x), ∀x ∈ [0 ;π/2 ).

Vì ∀x ∈ [0 ; π/2) nên tanx + x ≥ 0 và tanx – x >0 (theo câu a). Do đó y’ ≥ 0, ∀x ∈ [0 ; π/2). Dễ thấy y’ = 0 ⇔ x = 0. Vậy hàm số luôn đồng biến trên [0 ; π/2). Từ đó : ∀x ∈ [0 ; π/2) thì g(x) > g(0) ⇔ tanx – x – x³/3 > tan0 – 0 – 0 = 0 hay tanx > x + x³/3.