1.\(\lim \left( {2n + 3} \right)\) bằng
A.\( + \infty .\) B.\(3.\)
C.\(5.\) D. \( – \infty .\)
2. Biết \(\lim \dfrac{{1 + {3^n}}}{{{3^{n + 1}}}} = \dfrac{a}{b}\) ( a,b là hai số tự nhiên và\(\dfrac{a}{b}\) tối giản). Giá trị của \(a + b\)bằng
A.\(3.\) B.\(\dfrac{1}{3}.\)
C.\(0.\) D. \(4.\)
3.\(\mathop {\lim }\limits_{x \to 1} ({x^2} – 2x – 3)\) bằng
A.\( – 5.\) B.\(0.\)
C.\(4.\) D. \( – 4.\)
4. Biết \(\mathop {\lim }\limits_{x \to – \infty } \dfrac{{x + 2}}{{1 – 2x}} = – \dfrac{a}{b}\) ( a,b là hai số tự nhiên và\(\dfrac{a}{b}\) tối giản). Giá trị của \(a – b\)bằng
A.\(3.\) B.\( – 1.\)
C.\( – 3.\) D. \(1.\)
5.\(\lim \dfrac{{2n + 3}}{{{n^2} + 2n + 4}}\) bằng
A.\(2.\) B.\(1.\)
C.\(0.\) D. \( + \infty .\)
6.Biết rằng phương trình \({x^5} + {x^3} + 3x – 1 = 0\)có duy nhất 1 nghiệm \({x_0},\)mệnh đề nào dưới đây đúng?
A.\({x_0} \in \left( {0;1} \right).\)
B. \({x_0} \in \left( { – 1;0} \right).\)
C. \({x_0} \in \left( {1;2} \right).\)
D. \({x_0} \in \left( { – 2; – 1} \right).\)
7. Cho hàm số \(y = {x^3} – 2{x^2} + 3x + 2.\)Giá trị của \(y’\left( 1 \right)\)bằng
A.\(7.\) B.\(4.\)
C.\(2.\) D. \(0.\)
8. Đạo hàm của hàm số \(y = \sin 2x\)bằng
A.\(y’ = \cos 2x.\)
B. \(y’ = 2\cos 2x.\)
C. \(y’ = – 2\cos 2x.\)
D. \(y’ = – \cos 2x.\)
9. Đạo hàm của hàm số \(y = \dfrac{{x + 1}}{{x – 1}}\)bằng
A.\(y’ = \dfrac{{ – 2}}{{{{\left( {x – 1} \right)}^2}}}.\)
B. \(y’ = 1.\)
C. \(y’ = \dfrac{2}{{{{\left( {x – 1} \right)}^2}}}.\)
Advertisements (Quảng cáo)
D. \(y’ = \dfrac{{ – 2}}{{x – 1}}.\)
10.Đạo hàm của hàm số \(y = \sqrt {{x^2} + 1} \)bằng
A. \(y’ = \sqrt {2x} .\)
B. \(y’ = \dfrac{x}{{2\sqrt {{x^2} + 1} }}.\)
C. \(y’ = \dfrac{1}{{2\sqrt {{x^2} + 1} }}.\)
D. \(y’ = \dfrac{x}{{\sqrt {{x^2} + 1} }}.\)
11.Biết \(AB\)cắt mặt phẳng\(\left( \alpha \right)\)tại điểm\(I\)thỏa mãn\(IA = 3IB,\)mệnh đề nào dưới đây đúng?
A.\(4d\left( {A,\left( \alpha \right)} \right) = 3d\left( {B,\left( \alpha \right)} \right).\)
B. \(3d\left( {A,\left( \alpha \right)} \right) = d\left( {B,\left( \alpha \right)} \right).\)
C. \(3d\left( {A,\left( \alpha \right)} \right) = 4d\left( {B,\left( \alpha \right)} \right).\)
D. \(d\left( {A,\left( \alpha \right)} \right) = 3d\left( {B,\left( \alpha \right)} \right).\)
12. Mệnh đề nào dưới đây sai?
A. Đường thẳng vuông góc với mặt phẳngkhi và chỉ khi góc giữa chúng bằng \({90^{\rm{o}}}.\)
B. Góc giữa hai đường thẳng bằng góc giữa 2 vectơ chỉ phương của 2 đường thẳng đó.
C. Hai mặt phẳng vuông góc với nhau khi và chỉ khi góc giữa chúng bằng \({90^{\rm{o}}}.\)
D. Góc giữa hai mặt phẳng là góc giữa 2 đường thẳng lần lượt vuông góc với 2 mặt phẳng đó.
B. PHẦN TỰ LUẬN (7đ):
1.(1đ). Tính các giới hạn sau:
a.\(\mathop {\lim }\limits_{x \to – \infty } \left( {{x^3} – 2{x^2} + x + 1} \right);\)
b.\(\mathop {\lim }\limits_{x \to 3} \dfrac{{\sqrt {x + 1} – 2}}{{x – 3}}.\)
Câu 2 (1đ). Tính đạo hàm cấp 1 của mỗi hàm số sau:
Advertisements (Quảng cáo)
a.\(y = \left( {x + 2\sqrt x } \right)\left( {{x^2} + 4} \right);\)
b. \(y = {\cot ^2}\dfrac{2}{x} + \tan \dfrac{{x + 1}}{2}.\)
Câu 3 (1đ).Tìm giá trị của tham số a để hàm số \(f(x) = \left\{ \begin{array}{l}\dfrac{{{x^2} + 4x – 5}}{{x – 1}}\,\,khi\,\,x \ne 1\\2x + a\,\,\,\,\,\,\,\,\,\,\,\,\,khi\,\,x = 1\end{array} \right.\)liên tục tại\({x_0} = 1.\)
4. (1đ). Cho hàm số\(f\left( x \right) = \cos 2x.\)Gọi \(\left( C \right)\)là đồ thị của hàm số \(y = {f^{\left( {50} \right)}}\left( x \right).\) Viết phương trình tiếp tuyến của\(\left( C \right)\) tại điểm có hoành độ \(x = \dfrac{\pi }{6}.\)
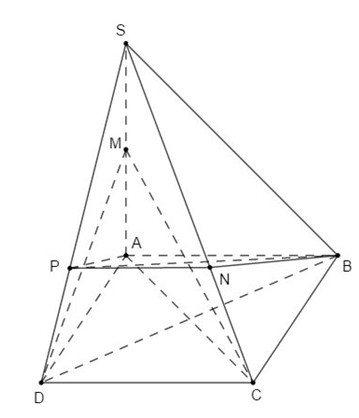
5. (3đ). Cho hình chóp\(S.ABCD\) có đáy \(ABCD\) là hình vuông cạnh \(a,\) \(SA \bot \left( {ABCD} \right)\) và góc giữa \(SD\) với mặt đáy bằng \({45^{\rm{o}}}.\) Gọi \(M,N,P\) lần lượt là các điểm trên cạnh \(SA,SC,SD\) sao cho \(SM = MA,\) \(SN = 2NC\) và \(SP = 2PD.\)
a. Chứng minh rằng \(\left( {SAC} \right) \bot BD;\)\(\left( {SAB} \right) \bot \left( {SBC} \right).\)
b. Chứng minh rằng \(AP \bot NP.\)
c. Tính côsin của góc giữa 2 mặt phẳng \(\left( {MCD} \right)\) và \(\left( {BNP} \right).\)

A. Phần trắc nghiệm:
| 1 | 2 | 3 | 4 | 5 | 6 |
| A | D | D | B | C | A |
| 7 | 8 | 9 | 10 | 11 | 12 |
| C | B | A | D | D | B |
B. Phần tự luận:
1.
a) \(\mathop {\lim }\limits_{x \to – \infty } \left( {{x^3} – 2{x^2} + x + 1} \right) = \)\(\mathop {\lim }\limits_{x \to – \infty } {x^3}\left( {1 – \dfrac{2}{x} + \dfrac{1}{{{x^2}}} + \dfrac{1}{{{x^3}}}} \right) = – \infty \)
b) \(\mathop {\lim }\limits_{x \to 3} \dfrac{{\sqrt {x + 1} – 2}}{{x – 3}} = \)\(\mathop {\lim }\limits_{x \to 3} \dfrac{{(\sqrt {x + 1} – 2)(\sqrt {x + 1} + 2)}}{{(x – 3)(\sqrt {x + 1} + 2)}} = \)\(\mathop {\lim }\limits_{x \to 3} \dfrac{1}{{\sqrt {x + 1} + 2}} = \dfrac{1}{4}\)
2.
a) \(y = \left( {x + 2\sqrt x } \right)\left( {{x^2} + 4} \right)\)
\(y’ = {\left( {x + 2\sqrt x } \right)^\prime }\left( {{x^2} + 4} \right) \)\(\,+ \left( {x + 2\sqrt x } \right){\left( {{x^2} + 4} \right)^\prime }\)
\( = \left( {1 + \dfrac{1}{{\sqrt x }}} \right)\left( {{x^2} + 4} \right)\)\(\, + 2x\left( {x + 2\sqrt x } \right)\)\( = 3{x^2} + 5x\sqrt x + \dfrac{4}{{\sqrt x }} + 4.\)
b) \(y = {\cot ^2}\dfrac{2}{x} + \tan \dfrac{{x + 1}}{2}\)
\(y’ = 2.\cot \dfrac{2}{x}{\left( {\cot \dfrac{2}{x}} \right)^\prime } + \dfrac{{{{\left( {\dfrac{{x + 1}}{2}} \right)}^\prime }}}{{{{\cos }^2}\dfrac{{x + 1}}{2}}}\)
\( = 2.\cot \dfrac{2}{x}\dfrac{{ – {{\left( {\dfrac{2}{x}} \right)}^\prime }}}{{{{\sin }^2}\dfrac{2}{x}}} + \dfrac{1}{{2c{\rm{o}}{{\rm{s}}^2}\dfrac{{x + 1}}{2}}}\)
\( = 4\cot \dfrac{2}{x}.\dfrac{1}{{{x^2}{{\sin }^2}\dfrac{2}{x}}} + \dfrac{1}{{2c{\rm{o}}{{\rm{s}}^2}\dfrac{{x + 1}}{2}}}\)
3.
\(f(x) = \left\{ \begin{array}{l}\dfrac{{{x^2} + 4x – 5}}{{x – 1}}\,\,\, & khi\,\,x \ne 1\\2x + a\,\,\,\,\,\,\,\,\,\,\,\,\,\, & khi\,\,x = 1\end{array} \right.\)
Ta có:
\(\mathop {\lim }\limits_{x \to 1} f(x) = \mathop {\lim }\limits_{x \to 1} \dfrac{{{x^2} + 4x – 5}}{{x – 1}}\)\( = \mathop {\lim }\limits_{x \to 1} \dfrac{{(x – 1)(x + 5)}}{{x – 1}} = \)\(\mathop {\lim }\limits_{x \to 1} \left( {x + 5} \right) = 6\)
\(f(1) = 2 + a\)
Để hàm số liên tục tại \({x_0} = 1\) thì \(\mathop {\lim }\limits_{x \to 1} f(x) = f\left( 1 \right) \Leftrightarrow \)\(2 + a = 6 \Leftrightarrow a = 4.\)
4.
Ta có \(\begin{array}{l}{f^{\left( {4k} \right)}} = {2^{4k}}c{\rm{os}}2x\\{f^{\left( {4k + 1} \right)}} = – {2^{4k + 1}}\sin 2x\\{f^{\left( {4k + 2} \right)}} = – {2^{4k + 2}}c{\rm{os}}2x\\{f^{\left( {4k + 3} \right)}} = {2^{4k + 3}}\sin 2x\end{array}\).
Do đó (C) là đồ thị hàm số \(y = {f^{\left( {50} \right)}}\left( x \right) = – {2^{50}}c{\rm{os}}2x\)
Ta có: \(y’ = {f^{\left( {51} \right)}}\left( x \right) = {2^{51}}\sin 2x.\)
Tiếp tuyến tại điểm \(x = \dfrac{\pi }{6}\) có phương trình:
\(y = y’\left( {\dfrac{\pi }{6}} \right)\left( {x – \dfrac{\pi }{6}} \right) + y\left( {\dfrac{\pi }{6}} \right)\)
\( \Leftrightarrow y = {2^{51}}\sin \dfrac{\pi }{3}\left( {x – \dfrac{\pi }{6}} \right) – {2^{50}}c{\rm{os}}\dfrac{\pi }{3}\)
\( \Leftrightarrow y = {2^{51}}\dfrac{{\sqrt 3 }}{2}\left( {x – \dfrac{\pi }{6}} \right) – {2^{50}}.\dfrac{1}{2}\)
\( \Leftrightarrow y = {2^{50}}\sqrt 3 \left( {x – \dfrac{\pi }{6}} \right) – {2^{49}}\)
\( \Leftrightarrow y = {2^{50}}.\sqrt 3 x – \dfrac{{{2^{50}}\sqrt 3 \pi }}{6} – {2^{49}}\)
5.
a)
\(\left\{ \begin{array}{l}BD \bot AC\\BD \bot SA\end{array} \right.\)\( \Rightarrow BD \bot (SAC)\)
\(\left\{ \begin{array}{l}BC \bot AB\\BC \bot SA\end{array} \right.\)\( \Rightarrow BC \bot (SAB) \Rightarrow \left( {SBC} \right) \bot \left( {SAB} \right).\)
b)
\(\dfrac{{SN}}{{NC}} = \dfrac{{SP}}{{PD}} = 2\)\( \Rightarrow NP//CD\left( 1 \right)\)
\(CD \bot \left( {SAD} \right) \Rightarrow CD \bot AP\left( 2 \right)\)
Từ (1) và (2) suy ra \(AP \bot NP.\)
c) Chỉ ra được mp\(\left( {SAD} \right)\) vuông góc với giao tuyến của 2 mp \(\left( {MCD} \right)\) và \(\left( {BNP} \right)\)
Tính được côsin bằng \(\dfrac{3}{5}.\).