1. : Trong một mặt phẳng có 5 điểm là các đỉnh của một hình ngũ giác đều. Hỏi tổng số đoạn thẳng và tam giác có thể lập được từ 5 điểm trên là:
A. 10. B. 80.
C. 20. D. 40.
2. : Trong các khẳng định sau, khẳng định nào đúng?
A. Nếu hai mặt phẳng phân biệt lần lượt chứa hai đường thẳng song song thì giao tuyến của chúng (nếu có) cùng song song với hai đường thẳng đó hoặc trùng với một trong hai đường thẳng đó.
B. Nếu ba mặt phẳng đôi một cắt nhau theo ba giao tuyến thì ba giao tuyến ấy hoặc đổng quy hoặc đôi một song song.
C. Nếu hai mặt phẳng phân biệt lần lượt chứa hai đường thẳng song song thì giao tuyến của chúng (nếu có) cũng song song với hai đường thẳng đó.
D. Hai đường thẳng cùng song song với một đường thẳng thứ ba thì song song với nhau.
3. : Rút ra một lá bài từ bộ bài 52 lá. Xác suất để rút được lá ách (A) là:
A. \(\dfrac{4}{{13}}\).
B. \(\dfrac{2}{{13}}\).
C. \(\dfrac{1}{{169}}\).
D. \(\dfrac{1}{{13}}\).
4. : Nếu \(C_n^3 = 35\) thì n có giá trị là:
A. 5. B. 7.
C. 6. D. 8.
5. : Cho đường thẳng a song song với mặt phẳng \(\left( \alpha \right)\). Nếu \(\left( \beta \right)\) chứa a và cắt \(\left( \alpha \right)\) theo giao tuyến b thì b và a là hai đường thẳng :
A. cắt nhau.
B. trùng nhau.
C. chéo nhau.
D. song song với nhau.
6. : Phương trình \(0! + 1.1! + 2.2! + 3.3! + … + n.n! = 362880\) có nghiệm n. Khi đó, hệ số của \({x^n}\) trong khai triển thành đa thức của \(P\left( x \right) = {\left( {{x^2} – {x^3} + 1} \right)^n}\) là:
A. 756.
B. 238.
C. 328.
D. 765.
7. : \(x = \dfrac{{8\pi }}{3} + k2\pi ,k \in Z\) là một họ nghiệm của phương trình nào sau đây?
A. \(2\cos x + 1 = 0\).
B. \(2\sin x + 1 = 0\).
C. \(2\cos x – 1 = 0\).
D. \(2\sin \,x + \sqrt 3 = 0\).
8. : Cho tứ diện ABCD. Trên các cạnh AB, BC, CD lần lượt lấy các điểm P, Q, R sao cho \(AP = \dfrac{1}{3}AB,\,\)\(BC = 3QC\), R không trùng với C, D. Gọi PQRS là thiết diện của mặt phẳng (PQR) với tứ diện ABCD. Khi đó PQRS là:
A. Hình thang cân.
B. Hình thang.
C. Một tứ giác không có cặp cạnh đối nào song song.
D. Hình bình hành.
9. : Cho phương trình \(\sin \,x – \sin \,2x + \sin 3x = 0\), nghiệm của phương trình là:
A. \(x = \pm \dfrac{\pi }{3} + k2\pi ,\,\,x = k\dfrac{\pi }{2},k \in Z\).
B. \(x = k\dfrac{\pi }{2} + k\pi ,k \in Z\).
C. Đáp số khác.
D. \(x = \pm \dfrac{\pi }{6} + k\pi ,k \in Z\).
1.0 : Số hạng tổng quát trong khai triển biểu thức \({\left( {x – \dfrac{2}{{{x^2}}}} \right)^{15}},\,\,\left( {x \ne 0} \right)\) là:
A. \({\left( { – 2} \right)^k}C_{15}^k{x^{15 – 3k}}\).
Advertisements (Quảng cáo)
B. \({2^k}C_{15}^k{x^{15 – 3k}}\).
C. \({2^k}C_{15}^k{x^{15 – 2k}}\).
D. \({\left( { – 2} \right)^k}C_{15}^k{x^{15 – 2k}}\).
1.1 : Gieo đồng tiền 2 lần. Số phần tử của biến cố để mặt ngửa xuất hiện ít nhất 1 lần là:
A. 6.
B. 5.
C. 3.
D. 4.
1.2 : Số hạng không chứa x trong khai triển \({\left( {x – \dfrac{1}{x}} \right)^{10}}\) là:
A. \( – C_{10}^5\).
B. \( – C_{10}^4\).
C. \(C_{10}^4\).
D. \(C_{10}^5\).
1.3 : Số số hạng trong khai triển \({\left( {1 + 3x} \right)^n}\), biết n là số tự nhiên thỏa mãn \(C_{n – 1}^4 – C_{n – 1}^3 – \dfrac{5}{4}A_{n – 2}^2 = 0\) là:
A. 13.
B. 11.
C. 10.
D. 12.
1.4 : A, B là hai biến cố của không gian mẫu \(\Omega \). Công thức nào sau đây sai?
A. \(P\left( {\overline A } \right) = 1 – P\left( A \right)\).
B. \(P\left( {\overline A .\overline B } \right) = P\left( {\overline A } \right).P\left( {\overline B } \right)\) (nếu A, B là hai biến cố độc lập).
C. \(P\left( {A \cup B} \right) = P\left( A \right) + P\left( B \right) – P\left( {A \cap B} \right)\).
D. \(P\left( A \right) = \dfrac{{n\left( \Omega \right)}}{{n\left( A \right)}}\).
1.5 : Xác suất bắn trúng mục tiêu của một vận động viên khi bắn viên đạn là 0,3. Người đó bắn hai viên một cách độc lập. Xác suất để một viên trúng và một viên trượt mục tiêu là:
A. 0,21.
B. 0,09.
C. 0,18.
D. 0,42.
1.6 : Cho tứ diện ABCD. P, Q lần lượt là trung điểm của AB, CD. Điểm R nằm trên cạnh BC sao cho BR = 2RC. Gọi S là giao điểm của mp (PQR) và AD. Khi đó:
Advertisements (Quảng cáo)
A.SA = 3SD.
B. SA = 2SD.
C. SA = SD.
D. 2SA = 3SD.
1.7 : Trong một môn học, cô giáo có 30 câu hỏi khác nhau trong đó 5 câu hỏi khó, 10 câu hỏi trung bình, 15 câu hỏi dễ. Hỏi có bao nhiêu cách để lập ra đề thi từ 30 câu hỏi đó, sao cho mỗi đề gồm 5 câu khác nhau và mỗi đề phải có đủ loại câu hỏi trong đó câu hỏi dễ không ít hơn 2 và số câu hỏi dễ luôn lớn hơn số câu hỏi trung bình là 2?
A. 56578.
B. 56875.
C. 22750.
D. 15837.
1.8 : Tính giá trị biểu thức \(S = C_{2017}^1 + C_{2017}^2 + C_{2017}^3 + C_{2017}^4 + … + C_{2017}^{2016}\).
A. \(S = {2^{2016}} – 1\).
B. \(S = {2^{2017}}\).
C. \(S = {2^{2017}} – 2\).
D. \(S = {2^{2017}} – 1\).
1.9 : Công thức tính số chỉnh hợp là:
A. \(A_n^k = \dfrac{{n!}}{{\left( {n – k} \right)!k!}}\).
B. \(A_n^k = \dfrac{{n!}}{{\left( {n – k} \right)!}}\).
C. \(C_n^k = \dfrac{{n!}}{{\left( {n – k} \right)!}}\).
D. \(C_n^k = \dfrac{{n!}}{{\left( {n – k} \right)!k!}}\).
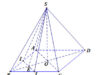
2.0 : (Chung giả thiết cho các câu từ 20 đến 23)
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. M, N, K lần lượt là trung điểm của các cạnh DC, BC, SA. Gọi H là giao điểm của AC và MN. Trong các khẳng định sau, khẳng định nào sai?
A. MN chéo SC.
B. MN // (SBD).
C. MN // (ABCD).
D. MN giao mặt (SAC) tại H.
2.1 : Giao tuyến của hai mặt phẳng (SAD) và (SBC) là đường thẳng d. Chọn câu trả lời đúng:
A. d // AB.
B. d // SO.
C.d qua S, O.
D. d // AD.
2.2 : Giao tuyến của (MNK) với (SAB) là đường thẳng KT, với T được xác định theo 4 phương án liệt kê dưới đây. Hãy chọn câu đúng:
A. T là giao điểm của MN với SB.
B. T là giao điểm của KN với SB.
C. T là giao điểm của MN với AB.
D. T là giao điểm của KN với AB.
2.3 : Gọi (P) là mặt phẳng qua H, song song với CD và SB, thiết diện tạo bởi (P) và hình chóp S.ABCD là hình gì?
A. Ngũ giác.
B. Hình bình hành.
C. Tứ giác không có cặp cạnh đối nào saong song.
D. Hình thang.
2.4 : Cho hình vuông ABCD. Trên cạnh AB lấy n điểm khác nhau, không trùng với A, B. Biết có 16 tam giác được tạo thành từ n + 4 điểm (A, B, C, D và n điểm nói trên). Giá trị của n bằng:
A. 5. B. 3.
C. 2. D. 4.
2.5 : Gieo một con súc sắc cân đối và đồng chất 2 lần. Xác suất của biến cố A sao cho tổng số chấm trong 2 lần bằng 8 là:
A. \(\dfrac{{13}}{{36}}\).
B. \(\dfrac{5}{{36}}\).
C. \(\dfrac{1}{3}\).
D. \(\dfrac{1}{6}\).
2.6 : Từ các số 1, 2, 3, 4, 5, 6, 7, 8, 9 có thể lập được bao nhiêu chữ số khác nhau sao cho hai số 1 và 2 luôn đứng cạnh nhau?
A. \(8!\). B. \(9!.2\).
C. \(8!.2\). D. \(9! – 2\).
2.7 : Cho hình chóp S.ABCD có đáy ABCD là hình thang (AB//CD), cạnh AB bằng 3a, AD = CD = a. Tam giác SAB cân tại S, SA = 2a. Mặt phẳng (P) song song SA, AB cắt các cạnh AD, BC, SC, SD theo thứ tự tại M, N, P, Q. Đặt AM = x ( 0 < x < a). Gọi x là giá trị để tứ giác MNPQ ngoại tiếp được một đường tròn, bán kính của đường tròn đó là:
A. \(\dfrac{{a\sqrt 7 }}{4}\).
B. \(\dfrac{{a\sqrt 7 }}{6}\).
C. \(\dfrac{{3a}}{4}\).
D. \(a\).
2.8 : Số cách sắp xếp 6 đồ vật khác nhau lên 6 chỗ theo hàng dọc là:
A. 720. B. 700.
C. 120. D. 6.
2.9 : Một mặt phẳng hoàn toàn được xác định nếu biết điều nào sau đây?
A. Một điểm và một đường thẳng thuộc nó.
. Ba điểm mà nó đi qua.
C. Ba điểm không thẳng hàng.
D. Hai đường thẳng thuộc mặt phẳng.
3.0 : Gieo 3 đổng tiền là một phép thử ngẫu nhiên có không gian mẫu là:
\(A.\left\{ {NNN,SSS,NNS,SSN,NSN,NSS,SNN} \right\}.\)
\(B.\left\{ {NN,NS,SN,SS} \right\}\).
\(C.\left\{ {NNN,SSS,NNS,SSN,NSN,SNS,NSS,SNN} \right\}.\)
\(D.\left\{ {NNN,SSS,NNS,SSN,NSN,SNS} \right\}.\)

| 1. C | 2. A | 3. D | 4. B | 5. D |
| 6. B | 7. A | 8. B | 9. A | 10. A |
| 11. A | 12. A | 13. B | 14. D | 15. D |
| 16. B | 17. C | 18. C | 19. B | 20. C |
| 21. D | 22. C | 23. D | 24. C | 25. B |
| 26. C | 27. B | 28. A | 29. C | 30. C |

![[Lương Ngọc Quyến] Đề thi học kì II Toán 11: Tìm số hạng đầu, công sai và tổng](https://dethikiemtra.com/wp-content/uploads/2017/04/de-thi-hoc-ki-2-lop-11-mon-toan-100x75.png)