
A. PHẦN TRẮC NGHIỆM (7đ)
1. : Tập xác định D của hàm số \(y = \dfrac{{2017}}{{1 + \cos x}}\)là
A. \(D = R{\rm{\backslash }}\left\{ {\pi + k2\pi ,k \in Z} \right\}\).
B. \(D = R{\rm{\backslash }}\left\{ {k2\pi ,k \in Z} \right\}\).
C. \(D = R{\rm{\backslash }}\left\{ { – \dfrac{\pi }{2} + k2\pi ,k \in Z} \right\}\).
D. \(D = R{\rm{\backslash }}\left\{ {\dfrac{\pi }{2} + k2\pi ,k \in Z} \right\}\).
2. : Hàm số \(y = {\sin ^2}x\left( {1 + \cos x} \right)\) là
A. Hàm số chẵn.
B. Hàm số lẻ.
C. Hàm số không chẵn, không lẻ.
D. Hàm số không xác định được tính chẵn lẻ.
3. : Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(y = \sin \,x + \cos x\). Giá trị của biểu thức \(P = M – m\) là:
A. \(P = 2\sqrt 2 \).
B. \(P = \sqrt 2 \).
C. \(P = 0\).
D. \(P = 2\).
4. : Tìm tất cả các giá trị thực của m để phương trình \(\cos x = m – 1\) có nghiệm.
A. \( – 1 \le m \le 1\).
B. \(m \ge 1\).
C. \(0 \le m \le 2\).
D. \(m \ge 2\).
5. : Tập nghiệm của phương trình \(\cos 4x = 0\) là
A. \(\left\{ {\dfrac{\pi }{2} + k\pi ,k \in Z} \right\}\).
B. \(\left\{ {\dfrac{\pi }{8} + k\pi ,k \in Z} \right\}\).
C. \(\left\{ {\dfrac{\pi }{8} + k\dfrac{\pi }{4},k \in Z} \right\}\).
D. \(\left\{ {\dfrac{\pi }{8} + k\dfrac{\pi }{2},k \in Z} \right\}\).
6. : Tập nghiệm của phương trình \(\tan 2x = \dfrac{{\sqrt 3 }}{3}\)là:
A. \(\left\{ {\dfrac{\pi }{6} + k\dfrac{\pi }{2},k \in Z} \right\}\).
B. \(\left\{ {\dfrac{\pi }{{12}} + k\dfrac{\pi }{2},k \in Z} \right\}\).
C. \(\left\{ {\dfrac{{2\pi }}{3} + k\pi ,k \in Z} \right\}\).
D. \(\left\{ {\dfrac{\pi }{3} + k\pi ,k \in Z} \right\}\).
7. : Tìm tất cả các giá trị thực của m để phương trình \(2\sin \,x – \left( {2m + 2} \right)\cos x = 2m – 3\) có nghiệm.
A. \(m < \dfrac{1}{{20}}\).
B. \(m \ge \dfrac{1}{{20}}\).
C. \(m \le \dfrac{1}{{20}}\).
D. \(m > \dfrac{1}{{20}}\).
8. : Tập nghiệm của phương trình \(2{\cos ^2}2x – 5\cos 2x + 2 = 0\) là:
A. \(\left\{ { \pm \dfrac{\pi }{6} + k\pi ,k \in Z} \right\}\).
B. \(\left\{ { \pm \dfrac{\pi }{6} + k2\pi ,k \in Z} \right\}\).
C. \(\left\{ { \pm \dfrac{\pi }{3} + k\pi ,k \in Z} \right\}\).
D. \(\left\{ { \pm \dfrac{\pi }{3} + k2\pi ,k \in Z} \right\}\).
9. : Từ các chữ số \(1;2;3;4;5;6\) có thể lập được bao nhiêu số chẵn có 3 chữ số đôi một khác nhau?
A. 60. B. 120.
C. 720. D. 48.
1.0 : Một hộp chứa các viên bi khác nhau gồm 6 viên bi đỏ, 9 viên bi xanh và 5 viên bi vàng. Hỏi có bao nhiêu cách chọn ra 3 viên bi có đủ cả ba màu?
A. 1140. B. 270.
C. 6840. D. 870.
1.1 : Trong các công thức sau, công thức nào sai?
A. \(C_n^k = \dfrac{{n!}}{{k!\left( {n – k} \right)!}}\).
B. \({P_n} = n!\).
C. \(C_n^k = C_n^{k – n}\).
Advertisements (Quảng cáo)
D. \(A_n^k = \dfrac{{n!}}{{\left( {n – k} \right)!}}\).
1.2 : Có bao nhiêu các sắp xếp một nhóm có 7 em học sinh thành một hàng dọc sao cho em nhóm trưởng luôn đứng đầu hàng hoặc cuối hàng?
A. 1140. B. 720.
C. 240. D. 120.
1.3 : Có bao nhiêu số tự nhiên có 3 chữ số đôi một khác nhau mà các chữ số đều là số chẵn?
A. 48. B. 60.
C. 360. D. 80.
1.4 : Hệ số của \({x^6}\) trong khai triển thành đa thức của \({\left( {2 – 3x} \right)^{10}}\) là:
A. \(C_{10}^6{2^4}{\left( { – 3x} \right)^6}\).
B. \( – C_{10}^6{2^4}{3^6}\).
C. \(C_{10}^6\).
D. \(C_{10}^6{2^4}{3^6}\).
1.5 : Hệ số của \({a^3}{b^4}\) trong khai triển thành đa thức của \({\left( {a + b} \right)^7}\)là:
A. 20. B. 21.
C. 35. D. 42.
1.6 : Phép thử tung ba đồng xu cân đối đồng chất. Khi đó số phần tử của không gian mẫu là:
A. 6. B. 8.
C. 12. D. 36.
1.7 : Chọn ngẫu nhiên một số tự nhiên có 2 chữ số nhỏ hơn 50. Tính xác suất của biến cố \(A\): “số được chọn là số nguyên tố”.
A. \(P\left( A \right) = \dfrac{{11}}{{40}}\).
B. \(P\left( A \right) = \dfrac{2}{{15}}\).
C. \(P\left( A \right) = \dfrac{6}{{25}}\).
D. \(P\left( A \right) = \dfrac{{12}}{{49}}\).
1.8 : Hai xạ thử bẵn mỗi người một viên đạn vào bia, xác suất bắn trúng vòng 10 của xạ thủ thứ nhất là 0,75 và xác suất bắn trúng vòng 10 của xạ thủ thứ hai là 0,85. Tính xác suất của biến cố A: “Có đúng một viên đạn trúng vòng 10”.
A. \(P\left( A \right) = 0,325\).
B. \(P\left( A \right) = 0,6375\).
C. \(P\left( A \right) = 0,0375\).
D. \(P\left( A \right) = 0,9625\).
1.9 : Trong mặt phẳng tọa độ Oxy, cho đường tròn \(\left( C \right):{\left( {x + 1} \right)^2} + {\left( {y – 2} \right)^2} = 4\) và vectơ \(\overrightarrow u \left( {1; – 3} \right)\). Ảnh của đường tròn (C) qua phép tịnh tiến theo vectơ \(\overrightarrow u \) là đường tròn
A. \(\left( {C’} \right):{x^2} + {\left( {y + 1} \right)^2} = 4\).
B. \(\left( {C’} \right):{\left( {x – 1} \right)^2} + {\left( {y + 1} \right)^2} = 4\).
C. \(\left( {C’} \right):{\left( {x – 2} \right)^2} + {\left( {y + 1} \right)^2} = 4\).
D. \(\left( {C’} \right):{\left( {x – 2} \right)^2} + {\left( {y – 1} \right)^2} = 4\).
2.0 : Cho tam giác đều ABC có tâm O. Phép quay tâm O, góc quay \(\varphi \) biến tam giác ABC thành chính nó. Khi đó một góc \(\varphi \) thỏa mãn là:
Advertisements (Quảng cáo)
A. \(\varphi = 60^\circ \).
B. \(\varphi = 90^\circ \).
C. \(\varphi = 120^\circ \).
D. \(\varphi = 180^\circ \).
2.1 : Trong mặt phẳng tọa độ Oxy, cho điểm \(A\left( {2; – 1} \right)\). Ảnh của A qua phép quay tâm O, góc quay \(90^\circ \) là:
A. \(A’\left( {1;2} \right)\).
B. \(A’\left( { – 1;2} \right)\).
C. \(A’\left( { – 2;1} \right)\).
D. \(A’\left( { – 1; – 2} \right)\).
2.2 : Phát biểu nào sau đây là sai?
A. Phép dời hình là phép biến hình bảo toàn khoảng cách giữa hai điểm bất kì.
B. Phép dời hình biến đường tròn thành đường tròn có cùng bán kính.
C. Phép dời hình biến đường thẳng thành đường thẳng song song với nó.
D. Phép dời hình biến ba điểm thẳng hàng thành ba điểm thẳng hàng và bảo toàn thứ tự giữa các điểm.
2.3 : Cho tam giác ABC có trọng tâm G. Gọi A’, B’, C’ lần lượt là trung điểm của các cạnh BC, CA, AB. Phép vị tự tâm G biến tam giác ABC thành tam giác A’B’C’ có tỉ số vị tự bằng bao nhiêu?
A. \( – \dfrac{1}{2}\). B. \(\dfrac{1}{2}\).
C. \(\dfrac{2}{3}\). D. \( – \dfrac{1}{3}\).
2.4 : Trong mặt phẳng tọa độ Oxy, cho đường tròn \(\left( C \right):{\left( {x – 1} \right)^2} + {\left( {y – 2} \right)^2} = 4\). Ảnh của \(\left( C \right)\) qua phép vị tự tâm \(I\left( {2; – 2} \right)\) tỉ số vị tự bằng 3 là đường tròn có phương trình:
A. \({\left( {x + 1} \right)^2} + {\left( {y – 10} \right)^2} = 36\).
B. \({\left( {x – 2} \right)^2} + {\left( {y – 6} \right)^2} = 36\).
C. \({\left( {x – 1} \right)^2} + {\left( {y – 10} \right)^2} = 36\).
D. \({\left( {x – 2} \right)^2} + {\left( {y + 4} \right)^2} = 36\).
2.5 : Yếu tố nào sau đây xác định một mặt phẳng duy nhất?
A. Ba điểm phân biệt.
B. Một điểm và một đường thẳng.
C. Hai đường thẳng cắt nhau.
D. Bốn điểm phân biệt.
2.6 : Trong các mệnh đề sau đây, mệnh đề nào sai?
A. Hai mặt phẳng có một điểm chung thì chúng có vô số điểm chung khác nữa.
B. Hai mặt phẳng có một điểm chung thì chúng có một đường thẳng chung duy nhất.
C. Hai mặt phẳng phân biệt có một điểm chung thì chúng có một đường thẳng chung duy nhất.
D. Hai mặt phẳng cùng đi qua 3 điểm phân biệt không thẳng hàng thì hai mặt phẳng đó trùng nhau.
2.7 : Tứ diện ABCD. Gọi M là trung điểm của BC. N là điểm nằm trên đoạn thẳng AB sao cho NB = 2NA, P là điểm nằm trên đoạn thẳng CD sao cho \(PC = 3PD\), S là giao điểm của BD và MP, Q là giao điểm của SN và AD. Tính tỉ số \(\dfrac{{QD}}{{QA}}\).
A. \(\dfrac{4}{5}\). B. \(\dfrac{3}{4}\).
C. \(\dfrac{2}{3}\). D. \(\dfrac{1}{2}\).
2.8 : Cho tứ diện ABCD. Gọi I, J lần lượt thuộc các cạnh AD, BC sao cho IA = 2ID và JB = 2JC. Gọi (P) là mặt phẳng qua IJ và song song với AB. Thiết diện của mặt phẳng (P) và tứ diện ABCD là:
A. Hình thang.
B. Hình bình hành.
C. Hình tam giác.
D. Tam giác cân.
B. PHẦN TỰ LUẬN (3đ)
1. a) Giải phương trình lượng giác \(2\cos \left( {3x – \dfrac{\pi }{3}} \right) – 1 = 0\).
b) Giải phương trình lượng giác \(2{\cos ^2}x + \sin 2x – 2 = 0\).
2. a) Một lớp có 35 học sinh. Cần chọn một đội gồm 8 học sinh đi dự đại hội đoàn cấp trên, trong đó có một trưởng đoàn, một phó đoàn, một thư kí và còn lại là các thành viên. Hỏi có bao nhiêu cách chọn học sinh đi dự đại hội?
b) Một chiếc hộp đựng 22 viên bi kích thước như nhau, trong đó có 7 viên bi màu xanh, 6 viên bi màu đen, 5 viên bi màu đỏ và 4 viên bi màu trắng. Chọn ngẫu nhiên ra 4 viên bi, tính xác suất để lấy được ít nhất 2 viên bi cùng màu.
3. Cho hình chóp \(S.ABCD\) có đáy ABCD là hình bình hành tâm O. Gọi E, F, G lần lượt là trung điểm của SA, BC, SD.
a) Xác định giao tuyến d của hai mặt phẳng \(\left( {SAB} \right)\) và \(\left( {SCD} \right)\).
b) Chứng minh rằng EF // (GAO).

A. PHẦN TRẮC NGHIỆM (7đ)
|
1. A |
2. A |
3. A |
4. C |
5. C |
|
6. B |
7. B |
8. A |
9. A |
10. B |
|
11. C |
12. A |
13. A |
14. D |
15. C |
|
16. B |
17. A |
18. A |
19. A |
20. C |
|
21. A |
22. C |
23. A |
24. A |
25. C |
|
26. B |
27. C |
28. B |
|
|
B. PHẦN TỰ LUẬN (3đ)
1. a) Giải phương trình lượng giác \(2\cos \left( {3x – \dfrac{\pi }{3}} \right) – 1 = 0\)
Ta có:
\(\eqalign{
& 2\cos \left( {3x – {\pi \over 3}} \right) – 1 = 0 \cr
& \Leftrightarrow \cos \left( {3x – {\pi \over 3}} \right) = {1 \over 2} \cr
& \Leftrightarrow \left[ \matrix{
3x – {\pi \over 3} = {\pi \over 3} + k2\pi \hfill \cr
3x – {\pi \over 3} = – {\pi \over 3} + k2\pi \hfill \cr} \right. \cr
& \Leftrightarrow \left[ \matrix{
x = {{2\pi } \over 9} + k{{2\pi } \over 3} \hfill \cr
x = k{{2\pi } \over 3} \hfill \cr} \right.\,\,\left( {k \in Z} \right) \cr} \)
Tập nghiệm của phương trình đã cho là:\(\left\{ {\dfrac{{2\pi }}{9} + k\dfrac{{2\pi }}{3},\,\,k\dfrac{{2\pi }}{3},k \in Z} \right\}\).
b) Giải phương trình lượng giác \(2{\cos ^2}x + \sin 2x – 2 = 0\)
Ta có:
\(\eqalign{
& 2{\cos ^2}x + \sin 2x – 2 = 0 \cr
& \Leftrightarrow 2{\cos ^2}x – 2 + \sin 2x = 0 \cr
& \Leftrightarrow – 2{\sin ^2}x + 2\sin x\cos x = 0 \cr} \)
\(\eqalign{
& \Leftrightarrow – 2\sin \,x\left( {\sin \,x – \cos x} \right) = 0 \cr
& \Leftrightarrow \left[ \matrix{
\sin \,x = 0 \hfill \cr
\sin x – \cos x = 0 \hfill \cr} \right. \cr
& \Leftrightarrow \left[ \matrix{
\sin \,x = 0 \hfill \cr
\tan x = 1 \hfill \cr} \right. \cr
& \Leftrightarrow \left[ \matrix{
x = k\pi \hfill \cr
x = {\pi \over 4} + k\pi \hfill \cr} \right.\,\,\left( {k \in Z} \right) \cr} \)
Tập nghiệm của phương trình đã cho là:\(\left\{ {k\pi ,\dfrac{\pi }{4} + k\pi ,k \in Z} \right\}\).
2. a) Số cách chọn 1 trưởng đoàn là: 35 cách
Số cách chọn 1 phó đoàn là: 34 cách
Số cách chọn 1 thư kí là: 33 cách
Số cách chọn 5 thành viên còn lại là: \(C_{32}^5 = 201376\) cách
\(\Rightarrow\) Có tất cả 35.34.33.201376 = 7 908 035 520 cách chọn học sinh đi dự đại hội.
b) Một chiếc hộp đựng 22 viên bi kích thước như nhau, trong đó có 7 viên bi màu xanh, 6 viên bi màu đen, 5 viên bi màu đỏ và 4 viên bi màu trắng. Chọn ngẫu nhiên ra 4 viên bi, tính xác suất để lấy được ít nhất 2 viên bi cùng màu.
Số phần tử của không gian mẫu là: \(n\left( \Omega \right) = C_{22}^4 = 7315\)
Gọi A: “lấy được ít nhất 2 viên bi cùng màu”
\(\Rightarrow n\left( A \right) = C_7^2C_6^1C_5^1 + C_7^1C_6^2C_5^1 + C_7^1C_6^1C_5^2\)\(\; = 21.6.5 + 7.15.5 + 7.6.10 = 1575\)
\( \Rightarrow P\left( A \right) = \dfrac{{n\left( A \right)}}{{n\left( \Omega \right)}} = \dfrac{{1575}}{{7315}} = \dfrac{{45}}{{209}}\)
Xác suất của biến cố A: \(P\left( A \right) = \dfrac{{n\left( A \right)}}{{n\left( \Omega \right)}}\).
Cách giải:
a) Có tất cả 7 908 035 520 cách chọn học sinh đi dự đại hội.
b) Gọi A: “lấy được ít nhất 2 viên bi cùng màu”
\(P\left( A \right) = \dfrac{{n\left( A \right)}}{{n\left( \Omega \right)}} = \dfrac{{45}}{{209}}\).
3.
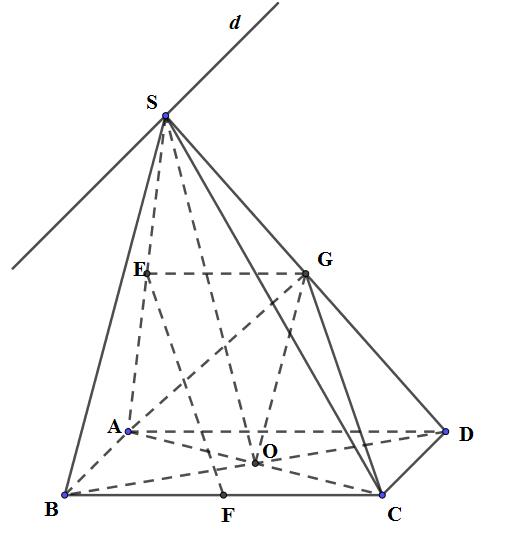
a) Ta có:
\(\left\{ \begin{gathered}
AB \subset \left( {SAB} \right) \hfill \\
CD \subset \left( {SCD} \right) \hfill \\
AB//CD \hfill \\
\left( {SAB} \right) \cap \left( {SCD} \right) = d \hfill \\
\end{gathered} \right. \Rightarrow d//AB//CD\)
Mặt khác \(S \in \left( {SAB} \right) \cap \left( {SCD} \right) \Rightarrow \) Giao tuyến d của hai mặt phẳng (SAB) và (SCD) là đường thẳng qua S và song song với AB.
b) O là tâm của hình bình hành ABCD , \( \Rightarrow\) O, A, C thẳng hàng \( \Rightarrow C \in \left( {GAO} \right)\)
Ta có: EG là đường trung bình của tam giác SAD \( \Rightarrow EG = \dfrac{1}{2}AD\)
Mà \(FC = \dfrac{1}{2}BC;\,\,AD = BC\)
\(\Rightarrow EG = FC \)
\(\Rightarrow EGCF\) là hình bình hành \( EF//\left( {GAC} \right)\) \( \Rightarrow EF//\left( {GAO} \right)\) (đpcm).






