
Phần I. Trắc nghiệm (2,0đ)
Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước phương án đó vào bài làm.
1. : Tập xác định D của hàm số \(y = 2\sin \left( {x – \dfrac{\pi }{3}} \right)\)
A. \(D = \left[ { – 1;1} \right]\)
B. \(D = \left[ { – 2;2} \right]\)
C. \(D = R\)
D. \(D = Z\)
2. : Tìm giá tị nhỏ nhất M của hàm số \(y = 1 – 2\cos x\).
A. \(M = – 1\)
B. \(M = 1\)
C. \(M = 3\)
D. \(M = – 3\)
3. : Trong mặt phẳng tọa độ Oxy, cho điểm \(M\left( {1; – 2} \right)\). Phép tịnh tiến theo vectơ \(\overrightarrow v \left( { – 1;1} \right)\) biến điểm M thành điểm N. Tìm toa độ điểm N.
A. \(N\left( {0; – 1} \right)\)
B. \(N\left( {2; – 3} \right)\)
C. \(N\left( { – 2;3} \right)\)
D. \(N\left( { – 1;0} \right)\)
4. : Cho tam giác ABC có trọng tâm G. Gọi M, N, P lần lượt là trung điểm của các cạnh AB, BC, CA. Phép vị tự nào sau đây biến \(\Delta ABC\) thành \(\Delta NPM\).
A. \({V_{\left( {A;\dfrac{1}{2}} \right)}}\)
B. \({V_{\left( {M;\dfrac{1}{2}} \right)}}\)
C. \({V_{\left( {G; – 2} \right)}}\)
D. \({V_{\left( {G; – \dfrac{1}{2}} \right)}}\)
5. : Có 10 cặp vợ chồng cùng tham dự chương trình Game show truyền hình thực tế. Có bao nhiêu cách chọn ra hai cặp đôi trong 10 cặp vợ chồng trên sao cho hai cặp đôi đó là hai cặp vợ chồng.
A. 19
B. 90
C. 45
Advertisements (Quảng cáo)
D. 190
6. : Trong khai triển của biểu thức \({\left( {{a^2} – \dfrac{1}{b}} \right)^7}\), số hạng thứ năm là:
A. \( – 35{a^6}{b^{ – 4}}\)
B. \(35{a^6}{b^{ – 4}}\)
C. \( – 21{a^4}{b^5}\)
D. \(21{a^4}{b^5}\)
7. : Cho hình chóp S.ABCD với đáy là tứ giác ABCD. Thiết diện của hình chóp cắt bởi mặt phẳng \(\left( \alpha \right)\) tùy ý không thể là:
A. Lục giác
B. Tứ giác
C. Ngũ giác
D. Tam giác
8. : Cho hình chóp S.ABCD có đáy là hình bình hành ABCD. Giao tuyến của 2 mặt phẳng \(\left( {SAD} \right)\) và \(\left( {SBC} \right)\) là đường thẳng song song với đường thẳng nào sau đây?
A. AC
B. BD
C. AD
D. SC
Phần II. Tự luận (8,0đ)
Advertisements (Quảng cáo)
1. (1,0đ): Giải phương trình \(\cos 5x.\cos x = \cos 4x\).
2. (1,5đ): Tìm số hạng không chứa x trong khai triển của biểu thức \({\left( {2x – \dfrac{1}{{{x^2}}}} \right)^{12}}\).
3. (1,5đ): Trong một đợt kiểm tra về vệ sinh an toàn thực phẩm của ngành ý tế tại chợ T, ban quản lý chợ cho lấy ra 12 mẫu thịt lớn trong đó có 3 mẫu ở quầy X, 4 mẫu ở quầy Y và 5 mẫu ở quầy Z. Mỗi mẫu này có khối lượng như nhau và để trong các hộp kín có kích thước giống hệt nhau. Đoàn kiểm tra lấy ngẫu nhiên ba hộp để phân tích, kiểm tra xem trong hộp thịt lợn có chứa chất tạo nạc Clenbuterol không. Tính xác suất để ba hộp lấy ra có đủ cả ba loại thịt ở các quầy X, Y và Z.
4. (3,0đ): Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Một mặt phẳng \(\left( \alpha \right)\) thay đổi luôn đi qua AB và cắt các cạnh SC, SD lần lượt tại M, N (M khác S, C và N khác S, D).
a) Chứng minh MN song song với mặt phẳng (ABCD).
b) Chứng minh giao điểm I của AM và BN thuộc một đường thẳng cố định.
c) Gọi K là giao điểm của AN và BM. Chứng minh \(\dfrac{{AB}}{{MN}} – \dfrac{{BC}}{{SK}} = 1\).
5. (1,0đ) Tìm tất cả các giá trị thực của tham số m để phương trình sau có nghiệm \(x \in \left[ {0;1} \right]\).
\(2{\sin ^2}\dfrac{{2x}}{{1 + {x^2}}} – \sin \dfrac{{2x}}{{1 + {x^2}}} – m = 0\).

Phần I. Trắc nghiệm (2,0đ)
|
1. C |
2. A |
3. A |
4. D |
5. B |
|
6. B |
7. A |
8. C |
|
|
Phần II. Tự luận (8,0đ)
1. \(\begin{array}{l}\cos 5x.\cos x = \cos 4x\\ \Leftrightarrow \dfrac{1}{2}\left( {\cos 6x + \cos 4x} \right) = \cos 4x\\ \Leftrightarrow \cos 6x + \cos 4x = 2\cos 4x\\ \Leftrightarrow \cos 6x = \cos 4x\\ \Leftrightarrow \left[ \begin{array}{l}6x = 4x + k2\pi \\6x = – 4x + k2\pi \end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}x = k\pi \\x = \dfrac{{k\pi }}{5}\end{array} \right. \Leftrightarrow x = \dfrac{{k\pi }}{5}\,\,\left( {k \in Z} \right)\end{array}\)
Vậy nghiệm của phương trình là \(x = \dfrac{{k\pi }}{5}\,\,\left( {k \in Z} \right)\).
2. \({\left( {2x – \dfrac{1}{{{x^2}}}} \right)^{12}}\)\(\, = \sum\limits_{k = 0}^{12} {C_{12}^k{{\left( {2x} \right)}^{12 – k}}{{\left( { – \frac{1}{{{x^2}}}} \right)}^k}} \)\(\, = \sum\limits_{k = 0}^{12} {C_{12}^k{2^{12 – k}}{x^{12 – k}}{{\left( { – 1} \right)}^k}{x^{ – 2k}}} \)\(\,= \sum\limits_{k = 0}^{12} {C_{12}^k{2^{12 – k}}{{\left( { – 1} \right)}^k}{x^{12 – 3k}}} \)
Để tìm hệ số của số hạng không chứa x \( \Leftrightarrow 12 – 3k = 0 \Leftrightarrow k = 4\).
Vậy số hạng không chứa x là: \(C_{12}^4{2^8}\).
3. Lấy ngẫu nhiên ra 3 hộp thịt từ 3 quầy có \(C_{12}^3 = 220\) cách \( \Rightarrow n\left( \Omega \right) = 220\).
Gọi A là biến cố: “3 hộp thịt được lấy đủ cả ba loại thịt ở các quầy X, Y, Z” \( \Rightarrow n\left( A \right) = 3.4.5 = 60\).
Vậy \(P\left( A \right) = \dfrac{{n\left( A \right)}}{{n\left( \Omega \right)}} = \dfrac{{60}}{{220}} = \dfrac{3}{{11}}\)
4.
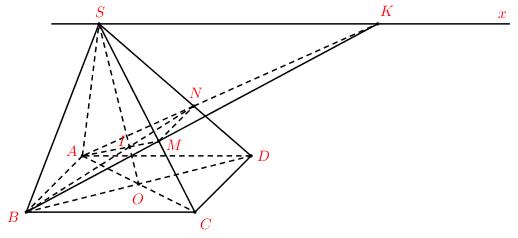
a) Ta có: AB // CD, \(CD \subset \left( {SCD} \right);\,\,AB \not\subset \left( {SCD} \right)\) nên \(AB//\left( {SCD} \right)\).
Do \(AB \subset \left( \alpha \right) \Rightarrow \left( \alpha \right) \cap \left( {SCD} \right) = MN//AB\).
Mặt khác \(AB \subset \left( {ABCD} \right)\) cùng giả thiết M khác S, C và N khác S, D \( \Rightarrow MN//\left( {ABCD} \right)\)
b) Gọi \(O = AC \cap BD\). Do \(I = AM \cap BN\) nên ta có
+) \(\left\{ \begin{array}{l}I \in AM\\AM \subset \left( {SAC} \right)\end{array} \right. \Rightarrow I \in \left( {SAC} \right)\)
+) \(\left\{ \begin{array}{l}I \in BN\\BN \subset \left( {SBD} \right)\end{array} \right. \Rightarrow I \in \left( {SBD} \right)\)
Suy ra I thuộc giao tuyến của 2 mặt phẳng (SAC); (SBD).
Mà \(\left( {SAC} \right) \cap \left( {SBD} \right) = SO \Rightarrow I \in SO\) cố định.
c) Gọi \(K = AN \cap BM\).
Xét \(\Delta AKB\) có AB // MN \( \Rightarrow \dfrac{{AB}}{{MN}} = \dfrac{{KB}}{{KM}} = \dfrac{{KM + BM}}{{KM}} = 1 + \dfrac{{BM}}{{KM}}\,\,\left( 1 \right)\)
Lại có \(\left\{ \begin{array}{l}BC \subset \left( {SBC} \right)\\AD \subset \left( {SAD} \right)\\BC//AD\end{array} \right. \Rightarrow \left( {SBC} \right) \cap \left( {SAD} \right) = Sx//AD//BC\)
Mà \(K = AN \cap BM;\,\,AN \subset \left( {SAD} \right);\,\,BM \subset \left( {SBC} \right)\)
\(\Rightarrow K \in Sx \Rightarrow SK//BC\).
Ta dễ dàng chứng minh được \(\Delta SKM \sim \Delta CBM \Rightarrow \dfrac{{BC}}{{SK}} = \dfrac{{BM}}{{KM}}\,\,\left( 2 \right)\)
Từ (1) và (2) \( \Rightarrow \dfrac{{AB}}{{MN}} = 1 + \dfrac{{BC}}{{SK}} \Rightarrow \dfrac{{AN}}{{MN}} – \dfrac{{BC}}{{SK}} = 1\)
5. Đặt \(u = \dfrac{{2x}}{{1 + {x^2}}}\). \(x \in \left[ {0;1} \right] \Rightarrow u \in \left[ {0;1} \right]\). Khi đó phương trình trở thành: \(2{\sin ^2}u – \sin u – m = 0\)
Đặt \(t = \sin u;\,\,u \in \left[ {0;1} \right] \Rightarrow t \in \left[ {0;\sin 1} \right]\), phương trình trở thành \(2{t^2} – t – m = 0 \Leftrightarrow 2{t^2} – t = m\,\,\left( * \right)\) (với \(t \in \left[ {0;\sin 1} \right]\)).
Số nghiệm của phương trình là số giao điểm của đồ thị hàm số \(f\left( t \right) = 2{t^2} – t\) (với \(t \in \left[ {0;\sin 1} \right]\)) và đường thẳng \(y = m\) song song với trục hoành.
Xét hàm số \(f\left( t \right) = 2{t^2} – t\) (với \(t \in \left[ {0;\sin 1} \right]\)) ta có BBT:
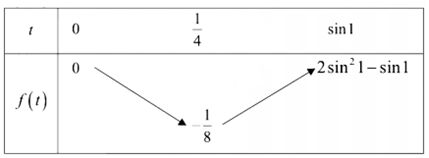
Khi đó phương trình (*) có nghiệm \(t \in \left[ {0;\sin 1} \right] \Leftrightarrow – \dfrac{1}{8} \le m \le 2{\sin ^2}1 – \sin 1\).





