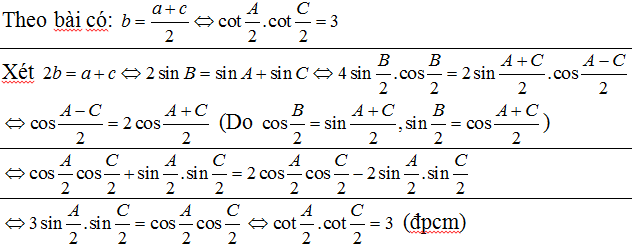1.Tìm số hạng đầu, công sai và tổng của 30 số hạng đầu tiên của cấp số cộng (un) biết:
2. a) Tính giới hạn: lim (√(n2 + 3n + 1) – n
b) Tìm m để hàm số :
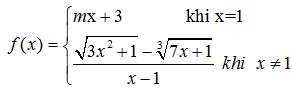liên tục tại x=1
c) Chứng minh phương trình x6 + 2sin 2x -1 = 0 luôn có nghiệm.
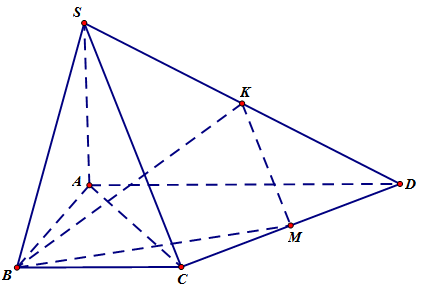
3.Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và B, mặt phẳng (SAB) và mặt phẳng (SAD) cùng vuông góc với mặt phẳng (ABCD),
AD = SA = 2a , AB = BC = a,
a) Chứng minh rằng: SA ⊥ (ABCD)
b) Chứng minh rằng: (SBC) ⊥ (SAB)
c) Tính góc giữa đường thẳng SC và mặt phẳng (ABCD).
d) Gọi M là trung điểm của cạnh C
D.Tính góc giữa hai đường thẳng BM và SC.
4. Cho tam giác ABC có AB = c, BC = a, CA = b. Chứng minh rằng ba cạnh a, b, c theo thứ tự tạo lập một cấp số cộng khi và chỉ khi ba số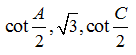 
theo thứ tự lập thành một cấp số nhân.
Advertisements (Quảng cáo)
ĐÁP ÁN VÀ HƯỚNG DẪN GIẢI ĐỀ THI HỌC KÌ 2
MÔN: TOÁN LỚP 11
1.
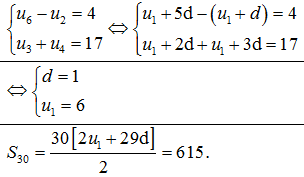
2.a)
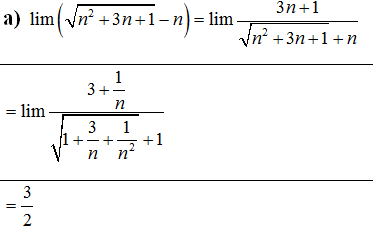
b) x= 1 thuộc tập xác định của hàm số
Advertisements (Quảng cáo)
Hàm số liên tục tại x=1 khi và chỉ khi 
+ f(x) = m + 3
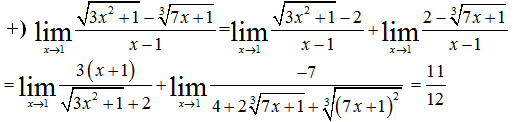
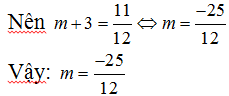
c) Xét hàm số g(x) = x6 + 2sin 2x -1 liên tục trên tập xác định R nên hàm số liên tục trên khoảng (0; π/2).
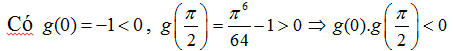
Nên phương trình x6 + 2sin 2x -1 = 0 luôn có nghiệm trong khoảng (0; π/2). (đpcm).
3. a)
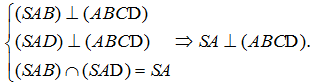
b)
c) Đường thẳng AC là hình chiếu của đường thẳng SC trên mp(ABCD)
Nên góc giữa đường thẳng SC và mặt phẳng (ABCD) bằng góc giữa 2 đường thẳng AC và SC => (SC,(ABCD)) => (SC,AC) = ∠SCA < 900 (vì tam giác SAC vuông tại A)
Vậy: góc giữa đường thẳng SC và mặt phẳng (ABCD) bằng α sao cho tan α = √2 , (a ≈ 54044’).
d) MK là đường trung bình của tam giác SCD => MK // SC => góc giữa hai đường thẳng BM và SC bằng góc giữa hai đường thẳng BM và MK.
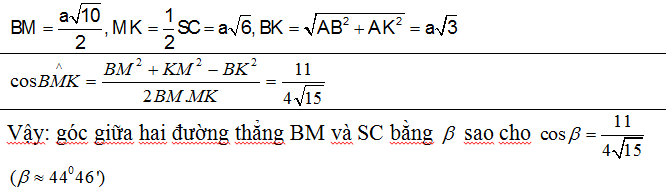
4. 
