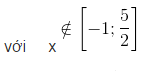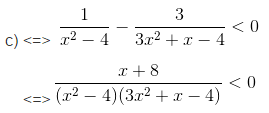Dấu của tam thức bậc hai – Chương 4 Toán Đại số 10
Giải bài 1,2,3,4 trang 105 SGK Đại số 10: Dấu của tam thức bậc hai
Bài 1. Xét dấu các tam thức bậc hai
a) 5x2 – 3x + 1; b) – 2x2 + 3x + 5;
c) x2 + 12x + 36; d) (2x – 3)(x + 5).
Giải:
a) ∆ = (- 3)2 – 4.5 < 0 => 5x2 – 3x + 1 > 0 ∀x ∈ R (vì luôn cùng dấu với 5 > 0).
b) – 2x2 + 3x + 5 = 0 <=> x1 = – 1, x2 = 5/2
– 2x2 + 3x + 5 = 0 với – 1 < x < 5/2
c) ∆’ = 62 – 36 = 0 => x2 + 12x + 36 > 0 ∀x ≠ – 6.
d) (2x – 3)(x + 5) = 0 <=> x1 = – 5, x2 = 3/2
Hệ số của tam thức bằng 2 > 0. Do đó:
Bài 2. Lập bảng xét dấu các biểu thức sau
a) f(x) = (3x2 – 10x + 3)(4x – 5);
b) f(x) = (3x2 – 4x)(2x2 – x – 1);
Advertisements (Quảng cáo)
c) f(x) = (4x2 – 1)(- 8x2 + x – 3)(2x + 9);
Giải: a) 3x2 – 10x + 3 = 0 <=> x1 = 1/3, x2 = 3
Bảng xét dấu:
Kết luận: f(x) < 0 với x ∈ (-∞; 1/3) ∪ (3; +∞).
b) Bảng xét dấu:
c) Ta có: – 8x2 + x – 3 < 0 ∀x (vì ∆ = 1 – 4.(- 3)(- 8) < 0, a = -8 <0).
Advertisements (Quảng cáo)
d) Ta có: 4x2 + x – 3 = 0 <=> x1 = – 1, x1 = 3/4
Bảng xét dấu:
Bài 3 trang 105. Giải các bất phương trình sau
a) 4x2 – x + 1 < 0; b) – 3x2 + x + 4 ≥ 0;
Giải: a) Tam thức f(x) = 4x2 – x + 1 có hệ số a = 4 > 0 biệt thức ∆ = 12 – 4.4 < 0. Do đó f(x) > 0 ∀x ∈ R.
Bất phương trình 4x2 – x + 1 < 0 vô nghiệm.
b) f(x) = – 3x2 + x + 4 = 0 <=> x1 = – 1, x2 = 4/3
– 3x2 + x + 4 ≥ 0 <=> – 1 ≤ x ≤ 4/3
c)
Lập bảng xét dấu vế trái:
Tập nghiệm của bất phương trình S = (-∞; – 8) ∪ (- 2; -4/3) ∪ (1; 2).
d) Tập nghiệm S =[- 2; 3].
Bài 4 trang 105 Đại số. Tìm các giá trị của tham số m để các phương trình sau vô nghiệm
a) (m – 2)x2 + 2(2m – 3)x + 5m – 6 = 0;
b) (3 – m)x2 – 2(m + 3)x + m + 2 = 0.
Giải: a) Với m = 2 phương trình trở thành 2x + 4 = 0 có 1 nghiệm. Loại giá trị m = 2.
Phương trình vô nghiệm nếu:
<=> m < 1 ∪ m > 3.
b) Với m = 3, phương trình trở thành: – 6x + 5 = 0 có nghiệm. Loại trường hợp m = 3.
Phương trình vô nghiệm vô khi và chỉ khi: