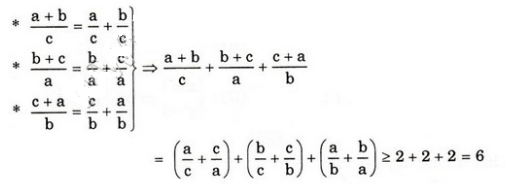Giải bài Ôn tập chương 4 Toán Đại số 10
Đáp án và Giải bài 1,2,3,4,5,6 trang 106; bài 7,8,9,10,11,12,13 trang 107 SGK Đại số 10: Ôn tập chương 4
Bài 1. Sử dụng dấu bất đẳng thức để viết các mệnh đề sau
a) x là số dương
b) y là số không âm
c) Với mọi số thực α, lαl là số không âm
d) Trung bình cộng của hai số dương a và b không nhỏ hơn trung bình nhân của chúng
Giải: a) x > 0
b) y ≥ 0
c) ∀α ∈ R, lal ≥ 0
Bài 2. Có thể rút ra kết luận gì về dấu của hai số a và b nếu biết
a) ab > 0 b) a/b > 0
c) ab < 0 d) a/b < 0
Bài 3. Trong các suy luận sau, suy luận nào đúng?
Giải: Có hai trường hợp:
Bài 4. Khi cân một vật với độ chính xác đến 0,05kg, người ta cho biết kết quả là 26,4kg. Hãy chỉ ra khối lượng thực của vật đó nằm trong khoảng nào.
Khối lượng thực của vật đó nằm trong:
(26,4 – 0,05 ; 26,4 + 0,05) (kg)
Bài 5 trang 106. Trên cùng một mặt phẳng tọa độ, hãy vẽ đồ thị hai hàm số y = f(x) = x + 1 và y = g(x) = 3 – x và chỉ ra các giá trị nào của x thỏa mãn:
a) f(x) = g(x)
b) f(x) > g(x)
c) f(x) < g(x)
Kiểm tra lại kết quả bằng cách giải phương trình, bất phương trình.
Advertisements (Quảng cáo)
Giải: a) f(x) = g(x)
⇔x + 1 = 3 – x ⇔ x = 1
b) f(x) > g(x)
⇔ x + 1 > 3 – x ⇔ x > 1
c) f(x) < g(x)
⇔ x + 1 < 3 – x ⇔ x < 1
Bài 6. Cho a,b,c là các số dương. Chứng minh rằng:
Giải:
Bài 7 trang 107. Điều kiện của một bất phương trình là gì? Thế nào là hai bất phương trình tương đương.
+ Điều kiện của một bất phương trình là tập hợp các giá trị của x để cho các phép tính trên bất đẳng thức có nghĩa
+ Hai bất phương trình có cùng tập nghiệm (có thể rỗng) là 2 bất phương trình tương đương. Ta thường gặp:
Phép cộng (trừ) (xem 1 trang 82 SGK)
Phép nhân (chia) (xem 2 trang 83 SGK)
Bài 8. Nêu quy tắc biểu diễn hình học tập nghiệm của bất phương trình ax + by ≤ c
Giải bất phương trình ax + by ≤ c
Bước 1: – Vẽ đồ thị Δ của ax + by = c
Bước 2: Lấy điểm Mo(x0;y0) ∉ Δ. Tính ax0 + by0
Bước 3: – So sánh ax0 + by0 với c
– Nếu ax0 + by0 ≤ c thì nửa mặt phẳng chứa Mo (xo;yo) là miền nghiệm của ax + by < c
– Nếu ax0 + by0 = c thì Δ là miền nghiệm
– Nếu ax0 + by0 > c thì nửa mặt phẳng bờ Δ chứa M không là miền nghiệm của ax + by ≤ c
Advertisements (Quảng cáo)
Bài 9. Phát biểu định lí về dấu của tam thức bậc hai
-Nếu biệt số Δ của tam thức bậc hai f(x) = ax² + bx + c ( a #0) là số âm thì a.f(x) > 0, ∀x ≠ -b/2a
– Nếu biệt số Δ > 0 thì
+ af(x) > 0 khi x ∉ (x1;x2)
+ f(x) < 0 khi x ∈ (x1;x2)
(x1,x2 là 2 nghiệm của f(x) với x1 < x2)
Bài 10 trang 107. Cho a > 0, b > 0 . Chứng minh rằng:
Giải:
Bài 11 trang 107 Toán Đại số 10. a) Bằng cách sử dụng hằng đẳng thức a² – b² = (a -b) (a +b) hãy xét dấu
f(x) = x4 – x2 + 6x – 9
và
b) Hãy tìm nghiệm nguyên của bất phương trình sau
x(x³ – x + 6) > 9
Giải bài 11:
Bảng xét dấu:
Bài 12. Cho a,b,c là độ dài ba cạnh của một tam giác. Sử dụng định lí về dấu của tam thức bậc hai, chứng minh rằng
b²x² – (b² + c² – a²)x + c² > 0 , với mọi x
Giải: Ta chỉ cần chứng minh tam thức:
b²x² – (b² + c² – a²)x + c² có biệt số Δ < 0, ∀x
Ta có: Δ = (b² + c² – a²)² – 4b²c²
= (b² + c² – a² + abc)(b² + c² – a² – 2bc)
= [(b + c)² – a²] [(b-c)² – a²] (1)
Mà a,b,c là ba cạnh của một tam giác nên
a + b > c => (b + c)² – a² > 0
Do đó, ta chỉ cần chứng minh (b – c)² – a² < 0
Ta có (b -c)² – a² = (b – c + a) (b – c – a) (2)
Mà a + b > c và b < a nên (2) cho (b – c)² – a² < 0
Vậy Δ < 0, ∀x
Bài 13. Biểu diễn hình học tập nghiệm của hệ bất phương trình bậc nhất hai ẩn: 
Giải:
Vẽ trên cùng một hệ trục tọa độ các đường thẳng:
Δ: 3x + y = 9
Δ1: x – y + 3 = 0
Δ2 : x + 2y = 8
Δ3: y = 6
Miền nghiệm là miền gạch chéo kể cả các đường biên của nó.