Cho ba điểm A, B, C liên tiếp trên một đường thẳng. Chứng minh rằng độ dài của nửa đường tròn đường kính AC bằng tổng các độ dài của hai nửa đường tròn có đường kính AB và B … trong Kiểm tra 15 phút môn Toán lớp 9 Chương 3 Hình học. Xem Đề và đáp án đầy đủ phía dưới đây
Cho ba điểm A, B, C liên tiếp trên một đường thẳng. Chứng minh rằng độ dài của nửa đường tròn đường kính AC bằng tổng các độ dài của hai nửa đường tròn có đường kính AB và BC.
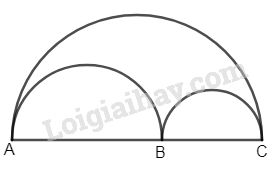
Gọi C1 là độ dài đường tròn đường kính AC, C2, C3 lần lượt là độ dài các đường tròn đường kính AB và BC.
Ta có : \(C_1= π.AC\);
Advertisements (Quảng cáo)
\(C_2= π.AB\);
\(C_3= π.BC\).
Vì B nằm giữa A và C nên \(AC = AB + BC\)
Advertisements (Quảng cáo)
Vậy \({C_2} + {C_3} = \pi AB + \pi BC \)\(\,= \pi \left( {AB + BC} \right) = \pi AC\)
\( \Rightarrow \dfrac{{{C_1}} }{ 2} =\dfrac {{{C_2} + {C_3}}}{ 2}\)
Nghĩa là độ dài của nửa đường tròn đường kính AC bằng tổng các độ dài của hai nửa đường tròn đường kính AB và BC.
