
Bài 1. Viết phương trình đường thẳng (d) qua điểm \(A\left( {1; – \sqrt 3 + 3} \right)\) và song song với đường thẳng \(y = – \sqrt 3 x.\) Tính góc tạo bởi đường thẳng (d) và trục \(Ox\).
Bài 2. Cho hàm số \(y = -x + 1\)
a. Vẽ đồ thị của hàm số
b. Tính góc tạo bởi đường thẳng \(y = -x + 1\) và trục hoành.

Bài 1. Đường thẳng (d) song song với đường thẳng \(y = – \sqrt 3 x\) nên phương trình của (d) có dạng : \(y = – \sqrt 3 x + b\) \((b ≠ 0)\)
\(A \in \left( d \right) \Rightarrow – \sqrt 3 + 3 = – \sqrt 3 .1 + b \)
Advertisements (Quảng cáo)
\(\Rightarrow b = 3\)
Vậy : \(y = – \sqrt 3 x + 3\)
Đường thẳng \(y = – \sqrt 3 x + 3\) (d) qua hai điểm \(M(0; 3)\), \(N\left( {\sqrt 3 ;0} \right)\) (xem hình vẽ)
Trong tam giác vuông OMN, ta có:
Advertisements (Quảng cáo)
\(\eqalign{ & OM = 3;ON = \sqrt 3 \cr & \Rightarrow \tan \widehat {MNO} = {{OM} \over {ON}} = \sqrt 3 \cr& \Rightarrow \widehat {MNO} = 60^\circ \cr& \Rightarrow \widehat {MNx} = 180^\circ – 60^\circ = 120^\circ . \cr} \)
Vậy góc giữa đường thẳng (d) và \(Ox\) bằng \(120^\circ \)
Bài 2.
a. Bảng giá trị:
|
x |
0 |
1 |
|
y |
1 |
0 |
Đường thẳng \(y = -x + 1\) qua hai điểm \(A(0; 1)\) và \(B(1; 0)\).
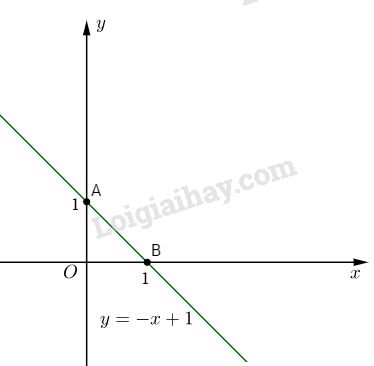
b. Tương tự bài 1, ta có góc giữa đường thẳng \(y = -x + 1\) và trục \(Ox\) bằng \(135^\circ \)






