Đề kiểm tra 15 phút lớp 9 môn Toán Chương 2 Hình học: Chứng minh AB là tiếp tuyến của đường tròn đường kính CD

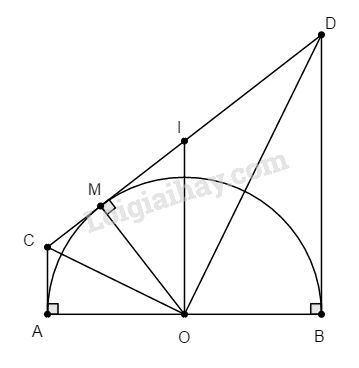
Cho nửa đường tròn (O; R) đường kính AB. Kẻ các tiếp tuyến tại A và B với nửa đường tròn. Qua điểm M thuộc nửa đường tròn (M khác A và B) kẻ tiếp tuyến thứ ba cắt các tiếp tuyến tại A và B lần lượt tại C và D.

a. Chứng minh rằng : \(CD = CA + BD\); \(\widehat {COD} = 90^\circ \)

b. Chứng minh AB là tiếp tuyến của đường tròn đường kính CD.

a. Ta có: \(CA = CM, DB = DM\) (tính chất của hai tiếp tuyến cắt nhau)

Mà \(CD = CM + DM \)\(\;⇒ CD = CA + BD\)

Lại có CO và DO là các tia phân giác của các góc kề bù \(\widehat {AOM}\) và \(\widehat {BOM}\) nên \(\widehat {COD} = 90^\circ \)

b. Gọi I là trung điểm của CD, ta có: OI là đường trung tuyến của tam giác vuông COD nên \(IO = IC = ID\).

hay OI là bán kính của đường tròn đường kính CD.

Dễ thấy tứ giác ABCD là hình thang vuông có OI là đường trung bình nên IO // AC và BD mà AC và BD cùng vuông góc với AB (gt)

\(⇒ IO ⊥ AB.\) Chứng tỏ AB là tiếp tuyến của đường tròn đường kính CD.