Cho tam giác đều ngoại tiếp đường tròn (I; r = 2cm).
a) Tính cạnh của tam giác đều.
b) Tính bán kính của đường tròn ngoại tiếp tam giác đó.
a)
Advertisements (Quảng cáo)
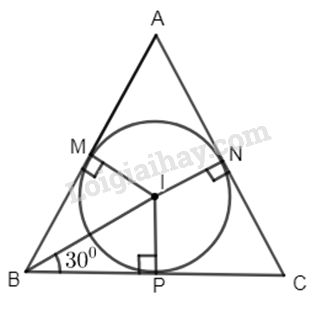
Ta có BM, BP là hai tiếp tuyến với đường tròn (I; r) nên BI là phân giác của \(\widehat {ABC}\)
\( \Rightarrow \widehat {IBP} = 30^\circ \).
Xét tam giác vuông IBP, ta có :
\(BP = IP.\cot 30^\circ = r\sqrt 3 \)
Advertisements (Quảng cáo)
Do đó : \(BC = 2r\sqrt 3 = 4\sqrt 3 \) cm
Vậy cạnh của tam giác đều ngoại tiếp đường tròn (I; r = 2cm) là \(4\sqrt 3 \) cm.
b) ∆IBP vuông tại P có \(\widehat {IBP} = 30^\circ \) nên \(BI = 2IP = 2r = 2.2 = 4\) (cm)
Tương tự ta tính được \(AI = CI = 4\) (cm)
\( \Rightarrow AI = BI = CI = 4\) (cm) nên I chính là tâm của đường tròn ngoại tiếp ∆ABC.
Do đó bán kính của đường tròn ngoại tiếp ∆ABC là 4 (cm).
