
Cho hai đường tròn (O) và (O’) tiếp xúc ngoài tại A. Đường thẳng OO’ cắt (O) và (O’) lần lượt tại B và C (khác A). Gọi DE là tiếp tuyến chung ngoài của (O) và (O’). Trong đó, \(D ∈ (O), E ∈ (O’)\). Gọi H là giao điểm của hai đường thẳng BD và CE. Chứng minh rằng :
a. \(\widehat {DHE} = 90^\circ \)
b. HA là tiếp tuyến chung của hai đường tròn (O) và (O’).

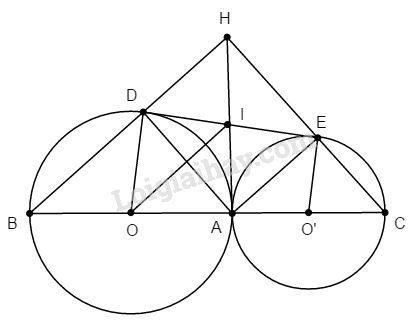
a. DE là tiếp tuyến chung ngoài của (O) và (O’) nên \(DE ⊥ OD\).
và \(DE ⊥ O’E ⇒ OD // O’E.\)
Advertisements (Quảng cáo)
Do đó: \(\widehat {DOO’} + \widehat {EO’O} = 180^\circ \) (cặp góc trong cùng phía)
\( \Rightarrow \widehat {DOB} + \widehat {EO’C} = 180^\circ \)
Các tam giác BOD và CO’E cân tại O và O’ nên:
\(2\widehat B + 2\widehat C = 180^\circ \)
\(\Rightarrow 2\left( {\widehat B + \widehat C} \right) = 180^\circ \Rightarrow \widehat B + \widehat C = 90^\circ \)
Advertisements (Quảng cáo)
Trong tam giác BHC ta có \(\widehat {BHC} = 90^\circ \,\,hay\,\,\widehat {DHE} = 90^\circ .\)
b. Dễ thấy tứ giác HDAE là hình chữ nhật (có ba góc vuông).
Gọi I là giao điểm hai đường chéo AH và DE, ta có \(ID = IA\) ( tính chất hai đường chéo hình chữ nhật).
Các tam giác ODI và OAI có : OI chung, \(DI = AI\) (cmt), \(OD = OA (=R)\)
Vậy \(∆ODI = ∆OAI\) (c.c.c)
\( \Rightarrow \widehat {OAI} = \widehat {ODI} = 90^\circ \) hay \(IA ⊥ BC\) tại A
\(⇒ HA\) là tiếp tuyến chung của (O) và (O’)

![[THCS Bình Giang] kiểm tra môn Sử lớp 9: Em hãy trình bày ngắn gọn diễn biến, kết quả của chiến dịch lịch sử Điện Biên Phủ năm 1954?](https://dethikiemtra.com/wp-content/uploads/2019/03/dongphongnha-100x75.jpg)




