Chia sẻ đề kiểm tra Toán 15 phút Chương 1 Hình học 9: Tính các cạnh của tam giác ABC vuông tại A

Cho \(∆ABC\) vuông tại A, biết \({{AB} \over {AC}} = {2 \over 3},\) đường cao \(AH = 6cm\). Tính các cạnh của tam giác

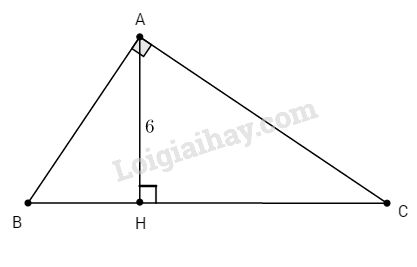
Ta có: \(∆AHB\) đồng dạng \(∆CHA\) (g.g) (vì có \(\widehat {BAH} = \widehat C\) (cùng phụ với \(\widehat B\) ))

\( \Rightarrow {{HA} \over {HC}} = {{AB} \over {AC}} = {2 \over 3} \)

\(\Rightarrow HC = {3 \over 2}HA = {3 \over 2}.6 = 9\,\left( {cm} \right)\)
Tương tự: \({{HA} \over {HB}} = {{AC} \over {AB}} = {3 \over 2}\)

\(\Rightarrow HB = {2 \over 3}HA = {2 \over 3}.6 = 4\,\left( {cm} \right)\)

Do đó: \(BC = HB + HC = 4 + 9 = 13 (cm)\)

\(∆ABC\) vuông tại A, đường cao AH.

\( \Rightarrow A{B^2} = BC.BH\) (định lí 1)

\( \Rightarrow AB = \sqrt {BC.BH}  = \sqrt {13.4}  = 2\sqrt {13} \)\(\;(cm)\)

Tương tự, ta có:

\(AC = \sqrt {BC.CH}  = \sqrt {13.9}  = 3\sqrt {13} \)\(\,\left( {cm} \right)\)

Cách khác: Gọi cạnh huyền là a và hai cạnh góc vuông là b, c; đường cao là h.

Ta có: \({c \over b} = {2 \over 3} \Rightarrow b = {3 \over 2}c\)

Mặt khác ∆ABC vuông có h là đường cao:

\(\eqalign{  & {1 \over {{h^2}}} = {1 \over {{b^2}}} + {1 \over {{c^2}}}\cr&hay\,\,{1 \over {{6^2}}} = {1 \over {{{\left( {{3 \over 2}c} \right)}^2}}} + {1 \over {{c^2}}}\cr& \Leftrightarrow {1 \over {{6^2}}} = {4 \over {9{c^2}}} + {1 \over {{c^2}}}  \cr  &  \Leftrightarrow {c^2} = 16 + 36\cr& \Leftrightarrow {c^2} = 52 \Leftrightarrow c = 2\sqrt {13} \,\left( {cm} \right) \cr} \)

Do đó \(b = {3 \over 2}.2\sqrt {13}  = 3\sqrt {13} \,\left( {cm} \right)\)