Luyện tập Diện tích hình tròn, hình quạt – Chương 3 hình 9: giải bài 83, 84 trang 99; Bài 85, 86, 87 trang 100 SGK Toán 9 tập 2.
Bài 83. a) Vẽ hình 62 (tạo bởi các cung tròn) với HI = 10cm và HO = 2cm. Nêu cách vẽ.

b) Tính diệntích hình HOABINH (miền gạch sọc)
c) Chứng tỏ rằng hình-tròn đường kính NA có cùng diệntích với hình HOABINH đó.
HD: a) Vẽ nửa đường-tròn đường kính HI = 10 cm, tâm M
Trên đường kính HI lấy điểm O và điểm B sao cho HO = BI = 2cm.
Vẽ hai nửa đường-tròn đường kính HO, BI nằm cùng phía với đường-tròn (M).
vẽ nửa đườngtròn đường kính OB nằm khác phía đối với đườngtròn (M). Đường thẳng vuông góc với HI tại M cắt (M) tại N và cắt đg tròn đường kính OB tại A.
b) S.hình HOABINH là:
½.π 52 +½ .π.32 – π.12 = 25/2π + 9/2π – π = 16π (cm2) (1)
c) S.hìnhtròn đường kính NA bằng:
π. 42 = 16π (cm2) (2)
So sánh (1) và (2) ta thấy hình-tròn kính NA có cùng diệntích với hình HOABINH
Bài 84. a) Vẽ lại hình tạo bởi các cung tròn xuất phát từ đỉnh C của tam giác đều ABC cạnh 1 cm. Nêu cách vẽ (h.63).
Advertisements (Quảng cáo)

b) Tính diệntích miền gạch sọc.
HD: a) Vẽ tam giác đều ABC cạnh 1cm
Vẽ 1/3 đg.tròn tâm A, bán kính 1cm, ta được cung CD
Vẽ 1/3 đg.tròn tâm B, bán kính 2cm, ta được cung DE
Vẽ 1/3 đg.tròn tâm C, bán kính 3cm, ta được cung EF
b) S.hìnhquạt CAD = 1/3. π.12
S.hìnhquạt DBE = 1/3 π.22
S.hình quạt ECF = 1/3 π.32
Advertisements (Quảng cáo)
S.phần gạch sọc = 1/3 π.12+ 1/3 π.22 + 1/3 π.32
= 1/3 π (12 + 22 + 32) = 14/3π ≈14,65 (cm2)
Bài 85. Hình viên phân là h.tròn giới hạn bởi một cung tròn và dây căng cung ấy. Hãy tính diện-tích hình viên phân AmB, biết góc ở tâm góc ∠AOB = 60o và bán kính đg tròn là 5,1 cm (h.64)
 ∆OAB là tam giác đều có cạnh bằng R = 5,1cm. Áp dụng công thức tính diệntích tam giác đều cạnh a là a2√3 / 4
∆OAB là tam giác đều có cạnh bằng R = 5,1cm. Áp dụng công thức tính diệntích tam giác đều cạnh a là a2√3 / 4
ta có S∆OBC = R2√3 / 4 (1)
S.hìnhquạt tròn AOB là: ΠR260o/360o = ΠR2/6 (2)
Từ (1) và (2) suy ra S.hìnhviênphân là: ΠR2/6 – R2√3 / 4 = R2(Π/6 – √3/4)
Thay R = 5,1 ta có Sviên phân ≈ 2,4 (cm2)
Bài 86. Hình vành khăn là phần h.tròn nằm giữa hai đường tròn đồng tâm (h.65).
a) Tính S.hìnhvànhkhăn theo R1 và R2 (giả sử R1 > R2).
b) Tính S.hìnhvànhkhăn khi R1 = 10,5 cm, R2 = 7,8 cm.

Giải: a)S.hìnhtròn (O;R1) là S1 = πR12.
S.hìnhtròn (O;R2) là S2 = πR22.
S.hìnhvànhkhăn là: S = S1 – S2 = πR12– πR22 = π( R12 – R22)
b) Thay số: S = 3,14. (10,52 – 7,82) = 155,1(cm2)
Bài 87 trang 100. Lấy cạnh BC của một tam giác đều làm đường kính, vẽ một nửa đường tròn về cùng một phía với tam giác ấy đối với đường thẳng BC. Cho biết cạnh BC = a, hãy diện tích hình viên phân được tạo thành.
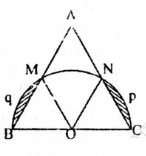
Gọi nửa đường-tròn tâm O đường kính BC căt hai cạnh AB và AC lần lượt tại M và N.
∆ONC có OC = ON, ∠C = 60o nên ∆ONC là tam giác đều, do đó ∠NOC = 60o.

S.hình viên phân:

Vậy S.hình viên phhân bên ngoài tam giác là: 



![[Thi văn kì 2 lớp 9 có đáp án] Cảm nhận của em về ước nguyện của Viễn Phương trong đoạn thơ…](https://dethikiemtra.com/wp-content/uploads/2019/04/vieng-lang-bac-100x75.jpg)