A. PHẦN TRẮC NGHIỆM (2đ)
1. Dãy số nào sau đây có giới hạn bằng 0?
A. \({\left( {\dfrac{5}{3}} \right)^n}\) B. \({\left( {\dfrac{1}{3}} \right)^n}\)
C. \({\left( { – \dfrac{5}{3}} \right)^n}\) D. \({\left( { – \dfrac{4}{3}} \right)^n}\)
2. Kết quả \(\lim \left( {5n – 3{n^3}} \right)\) bằng bao nhiêu ?
A. \( – \infty \) B. – 4
C. – 6 D. \( + \infty \)
3. Kết quả \(\mathop {\lim }\limits_{x \to 2} \dfrac{{{x^2} – 3x + 2}}{{2x – 4}}\) bằng bao nhiêu ?
A. \( + \infty \) B. \(\dfrac{3}{2}\)
C. \(\dfrac{1}{2}\) D. \( – \dfrac{1}{2}\)
4. Kết quả \(\mathop {\lim }\limits_{x \to – \infty } \dfrac{{{x^2} – x + 2}}{{{x^3} + 2x – 2}}\) bằng bao nhiêu ?
A. \( + \infty \) B. \(6\)
C. 0 D. \( – 1\)
5. Số gia của hàm số \(y = {x^3}\), ứng với: \({x_o} = 2\) và \(\Delta x = 1\) là:
A. 19 B. -7
C. 7 D. 0
6. Vi phân của hàm số \(y = \sin 3x\) là:
A. \(dy = – 3\cos 3x.dx\)
B. \(dy = 3\sin 3x.dx\)
C. \(dy = 3\cos 3x.dx\)
D. \(dy = – 3\sin 3x.dx\)
7. Đạo hàm của hàm số \(y = \sqrt {2x + 3} \) là:
A. \(\dfrac{{2x + 3}}{{2\sqrt {2x + 3} }}\) B. \(2\sqrt {2x + 3} \)
C. \(\dfrac{1}{{2\sqrt {2x + 3} }}\) D. \(\dfrac{1}{{\sqrt {2x + 3} }}\)
8. Tiếp tuyến của đồ thị hàm số \(y = – {x^3} + 2017\) tại điểm \(M\left( { – 2;2009} \right)\) có hệ số góc bằng bao nhiêu?
A. 12 B. -12
C. 192 D. -192
9. Khẳng định nào sau đây là đúng?
A.Vectơ chỉ phương của đường thẳng là vectơ có giá song song đường thẳng đó.
B. Góc giữa hai đường thẳng a và b là góc giữa hai đường thẳng a’ và b’ đi qua một điểm.
C. Hai đường thẳng vuông góc với nhau nếu góc giữa chúng bằng \({90^0}.\)
D. Hai đường thẳng vuông góc với nhau thì cắt nhau.
1.0: Khẳng định nào sau đây là đúng?
Advertisements (Quảng cáo)
A. Giữa hai mặt phẳng bất kì trong không gian có 4 vị trí tương đối
B. Nếu một đường thẳng vuông góc với hai đường thẳng cắt nhau cùng nằm trong một mặt phẳng thì nó vuông góc với mặt phẳng ấy.
C. Giữa hai đường thẳng bất kì trong không gian có 3 vị trí tương đối
D. Nếu một đường thẳng vuông góc với một đường thẳng nằm trong một mặt phẳng thì nó vuông góc với mặt phẳng ấy.
B. PHẦN TỰ LUẬN (8đ)
1. (1,0đ). Tính các giới hạn sau
a. \(\mathop {\lim }\limits_{x \to 2} \dfrac{{2 – x}}{{\sqrt {x + 7} – 3}}\)
b. \( \mathop {\lim }\limits_{x \to – 1} \dfrac{{\sqrt {4x + 8} – \sqrt[3]{{4{x^2} + 20x + 24}}}}{{{{\left( {x + 1} \right)}^2}}}\)
2. (1.0đ) Xét tính liên tục của hàm số
\(f(x) = \left\{ \begin{array}{l}\dfrac{{2{x^2} + 3x – 5}}{{x – 1}}{\rm{ }} khi{\rm{ }}x > 1\\3x{\rm{ + 1 }} khi{\rm{ }}x \le 1\end{array} \right.\) tại \(x = 1\)
3. (2,0đ)
a. Cho hàm số \(f\left( x \right) = \dfrac{{{x^4}}}{4} – \dfrac{{{x^3}}}{3} – \dfrac{{{x^2}}}{2} + \dfrac{1}{5}\). Giải bất phương trình
b. Cho hàm số \(f\left( x \right) = \sin 2x + x – 12\). Giải phương trình \(f’\left( x \right) = 0\)
4. (1đ)
Gọi ( C) là đồ thị hàm số : \(y = {x^3} + 4x + 2\). Viết phương trình tiếp tuyến của (C ) biết tiếp tuyến vuông góc với đường thẳng \(y = – \dfrac{1}{7}x – 4\)
5. (3,0đ).
Cho hình chóp S. ABCD có đáy ABCD là hình vuông cạnh 2a. Hình chiếu vuông góc của S lên (ABCD) trùng với trung điểm H của AB. Cạnh bên SA bằng \(a\sqrt 5 \)
a. Chứng minh rằng (SAD) vuông góc với (SAB).
b. Tính khoảng cách giữa AB và (SCD)
c. Tính khoảng cách giữa hai đường thẳng BD và SC

A. Phần trắc nghiệm (2đ)
Advertisements (Quảng cáo)
|
1. |
2. |
3. |
4. |
5. |
|
B |
A |
C |
A |
A |
|
6. |
7. |
8. |
9. |
10 |
|
C |
B |
D |
C |
B |
B. Phần tự luận (8đ)
1.
a. \(\mathop {\lim }\limits_{x \to 2} \dfrac{{2 – x}}{{\sqrt {x + 7} – 3}} \)
\(= \mathop {\lim }\limits_{x \to 2} \dfrac{{\left( {2 – x} \right)\left( {\sqrt {x + 7} + 3} \right)}}{{x – 2}}\)
\( = \mathop {\lim }\limits_{x \to 2} \left( {\sqrt {x + 7} + 3} \right) = 6\)
b. \( \mathop {\lim }\limits_{x \to – 1} \dfrac{{\sqrt {4x + 8} – \sqrt[3]{{4{x^2} + 20x + 24}}}}{{{{\left( {x + 1} \right)}^2}}}\)
\( = \mathop {\lim }\limits_{x \to – 1} \dfrac{{\sqrt {4x + 8} – \left( {x + 3} \right) + \left( {x + 3} \right) – \sqrt[3]{{4{x^2} + 20x + 24}}}}{{{{\left( {x + 1} \right)}^2}}}\)
\( = \mathop {\lim }\limits_{x \to – 1} \dfrac{{\sqrt {4x + 8} – \left( {x + 3} \right)}}{{{{\left( {x + 1} \right)}^2}}} + \mathop {\lim }\limits_{x \to – 1} \dfrac{{\left( {x + 3} \right) – \sqrt[3]{{4{x^2} + 20x + 24}}}}{{{{\left( {x + 1} \right)}^2}}}\)
\(\begin{array}{l} = \mathop {\lim }\limits_{x \to – 1} \dfrac{{ – {x^2} – 2x – 1}}{{{{\left( {x + 1} \right)}^2}\left[ {\sqrt {4x + 8} + x + 3} \right]}}\\ + \mathop {\lim }\limits_{x \to – 1} \dfrac{{{x^3} + 5{x^2} + 7x + 3}}{{{{\left( {x + 1} \right)}^2}\left[ {{{\left( {x + 3} \right)}^2} + \left( {x + 3} \right)\sqrt[3]{{4{x^2} + 20x + 24}} + \sqrt[3]{{{{\left( {4{x^2} + 20x + 24} \right)}^2}}}} \right]}}\end{array}\)
\(\begin{array}{l} = \mathop {\lim }\limits_{x \to – 1} \dfrac{{ – 1}}{{\left[ {\sqrt {4x + 8} + x + 3} \right]}}\\ + \mathop {\lim }\limits_{x \to – 1} \dfrac{{x + 3}}{{\left[ {{{\left( {x + 3} \right)}^2} + \left( {x + 3} \right)\sqrt[3]{{4{x^2} + 20x + 24}} + \sqrt[3]{{{{\left( {4{x^2} + 20x + 24} \right)}^2}}}} \right]}}\end{array}\)
\( = \dfrac{{ – 1}}{{12}}\)
2. Xét tính liên tục của hàm số tại điểm đã chỉ ra.
TXĐ: \(D = \mathbb{R}\)
\(\mathop {\lim }\limits_{x \to {1^ + }} f(x) = \mathop {\lim }\limits_{x \to {1^ + }} \dfrac{{2{x^2} + 3x – 5}}{{x – 1}}\)\(\, = \mathop {\lim }\limits_{x \to {1^ + }} \left( {2x + 5} \right) = 7\)
\(\mathop {\lim }\limits_{x \to {1^ – }} f(x) = \mathop {\lim }\limits_{x \to {1^ + }} \left( {3x + 1} \right) = 7 \)\(\,= \mathop {\lim }\limits_{x \to {1^ – }} f\left( x \right)\)
\( \Rightarrow \mathop {\lim }\limits_{x \to 1} f(x) = 7\)
\(f(1) = 7 = \mathop {\lim }\limits_{x \to 1} f(x)\)
Vậy hàm số liên tục tại \(x = 1\)
3.
a. \(f\left( x \right) = \dfrac{{{x^4}}}{4} – \dfrac{{{x^3}}}{3} – \dfrac{{{x^2}}}{2} + \dfrac{1}{5}\). Giải bất phương trình
\(f’\left( x \right) = {x^3} – {x^2} – x\)
\(f”\left( x \right) = 3{x^2} – 2x – 1\)
b. Cho hàm số \(f\left( x \right) = \sin 2x + x – 12\). Giải phương trình \(f’\left( x \right) = 0\)
\(f’\left( x \right) = 2{\rm{co}}{\mathop{\rm s}\nolimits} 2x + 1\)
\(f’\left( x \right) = 0 \)
\(\Leftrightarrow 2{\rm{co}}{\mathop{\rm s}\nolimits} 2x + 1 = 0\)
\(\Leftrightarrow {\rm{co}}{\mathop{\rm s}\nolimits} 2x = – \dfrac{1}{2}\)
\( \Leftrightarrow 2x = \pm \dfrac{{2\pi }}{3} + k2\pi \)
\(\Leftrightarrow x = \pm \dfrac{\pi }{3} + k\pi \)
4. Đường thẳng \(y = – \dfrac{1}{7}x – 4\) có hệ số góc bằng \( – \dfrac{1}{7}\)
\(y = {x^3} + 4x + 2 \Rightarrow y’ = 3{x^2} + 4\)
Tiếp tuyến vuông góc với đường thẳng \(y = – \dfrac{1}{7}x – 4\)nên tiếp tuyến có hệ số góc k thỏa \( – \dfrac{1}{7}.k = – 1 \Rightarrow k = 7\)
\( \Rightarrow 3{x^2} + 4 = 7 \Rightarrow x = \pm 1\)
Với \(x = 1 \Rightarrow y\left( 1 \right) = 7\) \( \Rightarrow PTTT: y = 7x\)
Với \(x = – 1 \Rightarrow y\left( { – 1} \right) = – 3\) \( \Rightarrow PTTT: y = 7x + 4\)
Vậy có 2 tiếp tuyến cần tìm là: \(y = 7x; y = 7x + 4\)
5.
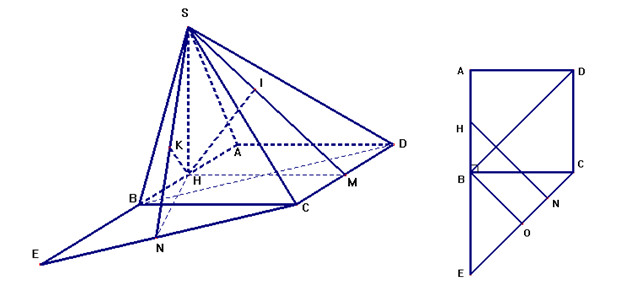
a. Ta có: \(AD \bot AB\)(vì ABCD là hình chữ nhật)
\(AD \bot AH \)(vì AH vuông góc với (ABCD))
\(\begin{array}{l} \Rightarrow AD \bot \left( {SAB} \right)\\ \Rightarrow \left( {SAD} \right) \bot \left( {SAB} \right)\end{array}\)
b. Trong \(\left( {ABCD} \right)\) kẻ \(HM \bot CD \Rightarrow CD \bot \left( {SHM} \right)\)
\( \Rightarrow \left( {SHM} \right) \bot \left( {SCD} \right); \left( {SHM} \right) \cap \left( {SCD} \right) = SM\)
Trong \(\left( {SHM} \right)\)kẻ \(HI \bot SC \Rightarrow HI \bot \left( {SCD} \right) \Rightarrow HI = d\left( {H,\left( {SCD} \right) } \right)\)
Có \(HM = 2a; SH = \sqrt {S{A^2} – H{A^2}} = 2a\)
\(HI = \dfrac{{SM.SH}}{{\sqrt {S{M^2} + S{H^2}} }} = \dfrac{{2a.2a}}{{\sqrt {4{a^2} + 4{a^2}} }} = a\sqrt 2 \)\(d\left( {H,\left( {SCD} \right) } \right) = a\sqrt 2 \)
c. Trong \(\left( {ABCD} \right)\) kẻ \(CE//BD; CE = BD, E \in AB\)
\(BD//CE \)\(\,\Rightarrow d\left( {BD,SC} \right) = d\left( {BD,\left( {SCE} \right)} \right) \)\(\,= d\left( {B,\left( {SCE} \right)} \right) = \dfrac{2}{3}d\left( {H,\left( {SCE} \right)} \right)\)
Trong \(\left( {ABCD} \right)\) kẻ \(HN \bot CE\), trong \(\left( {SCE} \right)\)kẻ \(HK \bot SN\)
\( \Rightarrow d\left( {H, \left( {SCE} \right)} \right) = HK\)
Kẻ \(BO \bot CE \Rightarrow BO = \dfrac{1}{2}AC = a\sqrt 2 \)
\(\Delta BEO\) đồng dạng với \(\Delta HEN\) \( \Rightarrow \dfrac{{HN}}{{BO}} = \dfrac{{BE}}{{HE}} = \dfrac{3}{2} \) \(\Rightarrow HN = \dfrac{3}{2}BO = \dfrac{{3a\sqrt 2 }}{2}\)
\(d\left( {H,\left( {SCE} \right) } \right) = HK \)\(\,= \dfrac{{SH.HN}}{{\sqrt {S{H^2} + H{N^2}} }} = \dfrac{{2a.\dfrac{{3a\sqrt 2 }}{2}}}{{\sqrt {4{a^2} + {{\dfrac{{9a}}{2}}^2}} }} \)\(\,= \dfrac{{6a\sqrt {17} }}{{17}}\)