1. Cho tứ diện \(ABCD\) có cạnh \(AD\) vuông góc với mặt phẳng \(\left( {ABC} \right)\) và cạnh \(BD\) vuông góc với cạnh \(BC\). Khi quay các cạnh tứ diện đó xung quanh trục là cạnh \(AB\), có bao nhiêu hình nón được tạo thành?
A. \(1.\) B. \(2.\)
C. \(3.\) D. \(4\).
2. Cho hình nón có đỉnh \(S\), độ dài đường sing bằng \(2a\). Một mặt phẳng qua đỉnh \(S\) cắt hình nón theo một thiết diện, diện tích lớn nhất của thiết diện là
A. \(2{a^2}.\) B. \({a^2}.\)
C. \(4{a^2}.\) D. \(\sqrt 3 {a^2}.\)
3. Cho hình nón có thiết diện qua trục là một tam giác đều. Khai triển hình nón theo một đường sinh, ta được một hình quạt tròn có góc ở tâm là \(\alpha \). Trong các kết luận sau, kết luận nào đúng ?
A. \(\alpha = \dfrac{\pi }{2}.\) B. \(\alpha = \dfrac{{2\pi }}{3}.\)
C. \(\alpha = \dfrac{{3\pi }}{4}.\) D. \(\alpha = \pi .\)
4. Cho hình trụ \(\left( H \right)\) có hai đáy là hai đường tròn \(\left( {O;\,r} \right)\) và \(\left( {O’;\,r} \right)\). Hình nón \(\left( N \right)\) có đỉnh là \(O\) và đáy của hình nón là đường tròn \(\left( {O’;\,r} \right)\). Lúc đó, tỉ số thể tích của khối trụ \(\left( H \right)\) và khối nón \(\left( N \right)\) bằng
A. \(\dfrac{1}{3}.\) B. \(3.\)
C. \(\dfrac{1}{2}.\) D. \(2.\)
5. Một hình thang vuông \(ABCD\) có đường cao \(AD = a\), đáy lớn \(CD = 2a\). Cho hình thang đó quay quanh \(CD\), ta được khối tròn xoay có thể tích bằng
A. \(V = \dfrac{4}{3}\pi {a^3}.\) B. \(V = 2\pi {a^3}.\)
C. \(V = \dfrac{1}{3}\pi {a^3}.\) D. \(V = 3\pi {a^3}.\)
6. Cho hình lăng trụ tứ giác đều có tất cả các cạnh bằng \(a\sqrt 2 \), cạnh bên bằng \(2a\). Xét hình trụ tròn xoay ngoiaj tiếp hình lăng trụ đó. Xét hai khẳng định sau
Thiết diện qua trục của hình trụ là một hình vuông.
Thể tích khối trụ là \(V = \pi {a^3}.\)
Hãy chọn phương án đúng.
A. Chỉ (I) đúng.
B. Chỉ (II) đúng.
C. Cả (I) và (II) đều sai.
D. cả (I) và (II) đều đúng.
7. Diện tích xung quanh của hình trụ bằng
A. một nửa tích của chu vi đáy với độ dài đường cao của nó.
B. hai lần tích của chu vi đáy với độ dài đường cao của nó.
C. một nửa tích của chu vi đáy với độ dài đường sinh của nó.
D. tích của chu vi đáy với độ dài đường sinh của nó.
8. Một khối cầu có diện tích đường tròn lớn là \(2\pi \) thì diện tích của khối cầu đó là
A. \(\dfrac{8}{3}\pi .\) B. \(4\pi .\)
C. \(8\pi .\) D. \(16\pi .\)
9. Cho điểm \(M\) nằm trong mặt cầu \(\left( S \right)\). Mệnh đề nào sau đây sai ?
A. Mọi mặt phẳng đi qua \(M\) đều cắt \(\left( S \right)\) theo một đường tròn.
B. Có một mặt phẳng đi qua \(M\) không cắt \(\left( S \right)\).
C. Mọi đường thẳng đi qua \(M\) đều cắt \(\left( S \right)\) tại hai điểm phân biệt.
D. Đường thẳng đi qua \(M\) và tâm \(O\) của mặt cầu cắt \(\left( S \right)\) tại hai điểm đối xứng nhau qua \(O\).
10: Hai khối cầu \(\left( {{O_1};\,{R_1}} \right)\) và \(\left( {{O_2};\,{R_2}} \right)\) có diện tích lần lượt là \({S_1},\,{S_2}\). Nếu \({R_2} = 2{R_1}\) thì \(\dfrac{{{S_2}}}{{{S_1}}}\) bằng
A. \(16.\) B. \(8.\)
C. \(4.\) D. \(2.\)
11: Trong số các mệnh đề sau, mệnh đề nào đúng?
Advertisements (Quảng cáo)
A. Tồn tại duy nhất một mặt cầu đi qua hai đường tròn nằm trong hai mặt phẳng cắt nhau.
B. Tồn tại duy nhất một mặt cầu đi qua hai đường tròn nằm trong hai mặt phẳng song song.
C. Tồn tại duy nhất một mặt cầu đi qua hai đường tròn cắt nhau.
D. Tồn tại duy nhất một mặt cầu đi qua hai đường tròn cắt nhau nằm trong hai mặt phẳng phân biệt.
12: Một đường thẳng \(d\) thay đổi, qua \(A\) và tiếp xúc với \(S\left( {O;R} \right)\) tại \(M\). Gọi \(H\) là hình chiếu của \(M\) lên đường thẳng \(OA\). Khi đó, điểm \(M\) thuộc mặt phẳng nào trong các mặt phẳng sau đây?
A. Mặt phẳng vuông góc với \(OA\) tại O.
B. . Mặt phẳng vuông góc với \(OA\) tại trung điểm \(OA\).
C. Mặt phẳng vuông góc với \(OA\) tại \(H\).
D. Mặt phẳng vuông góc với \(OA\) tại \(A\).
13: Một đường thẳng \(d\) thay đổi, qua \(A\) và tiếp xúc với \(S\left( {O;r} \right)\) tại \(M\), với \(OM = 2r\). Gọi \(H\) là hình chiếu của \(M\) lên đường thẳng \(OA\). Khi đó, độ dài đoạn thẳng \(MH\) bằng
A. \(\dfrac{{r\sqrt 2 }}{2}\). B. \(\dfrac{{r\sqrt 3 }}{3}\).
C. \(\dfrac{{r\sqrt 3 }}{2}\). D. \(\dfrac{{3r\sqrt 3 }}{4}\).
14: Giao tuyến của hai mặt cầu \(\left( S \right)\) và \(\left( {S’} \right)\) có thể là?
A. Đoạn thẳng, điểm.
B. Điểm, hình tròn.
C. Điểm, đường tròn.
D. Điểm, đường tròn, tập hợp rỗng.
15: Cho mặt nón \(\left( N \right)\) với góc ở đỉnh là \(60^\circ \). Trong các khẳng định sau, khẳng định nào sai?
A. Góc giữa đường sinh bất kì và trục của mặt nón \(\left( N \right)\) bằng \(30^\circ \).
B. Góc giữa hai đường sinh bất kì của mặt nón \(\left( N \right)\) bằng \(60^\circ \).
C. Mặt nón \(\left( N \right)\) chứa vô số đường sinh.
D. Góc giữa hai đường sinh đối xứng nhau qua trục của mặt nón \(\left( N \right)\) là \(60^\circ \).
16: Cho hai điểm cố định \(A,B\) cố định, \(M\) là điểm di động trong không gian sao cho góc giữa đường thẳng \(AB\) và \(AM\) bằng \(30^\circ \). Trong các mệnh đề sau, mệnh đề nào đúng ?
A. \(M\) thuộc mặt cầu cố định.
B. \(M\) thuộc mặt trụ cố định.
C. \(M\) thuộc mặt phẳng cố định.
Advertisements (Quảng cáo)
D. \(M\) thuộc mặt nón cố định.
17: Mệnh đề nào sau đây là mệnh đề sai?
A. Hình trụ luôn chứa một đường tròn.
B. Hình nón luôn chứa một đường tròn.
C. Hình nón luôn chứa một đường thẳng.
D. Mặt trụ luôn chứa một đường thẳng.
18: Cho hình lập phương \(ABCD.A’B’C’D’\) có cạnh \(a\). Diện tích xung quanh của hình nón tròn xoay sinh bởi đường gấp khúc \(AC’A’\) khi quay quanh trục \(AA’\) bằng?
A. \(\pi {a^2}\sqrt 2 .\) B. \(\pi {a^2}\sqrt 3 .\)
C. \(\pi {a^2}\sqrt 5 .\) D. \(\pi \sqrt 6 {a^2}.\)
19: Một hình nón có đường sinh bằng \(8{\rm{ cm}}\), diện tích xung quanh bằng \(240\pi {\rm{ c}}{{\rm{m}}^2}\). Đường kính của đường tròn đáy hình nón bằng
A. \(2\sqrt {30} {\rm{ cm}}{\rm{.}}\) B. \(30{\rm{ cm}}{\rm{.}}\)
C. \(60{\rm{ cm}}{\rm{.}}\) D. \(50{\rm{ cm}}{\rm{.}}\)
20: Cho điểm \(M\) cố định thuộc mặt phẳng \(\left( \alpha \right)\) cho trước, xét đường thẳng \(d\) thay đổi đi qua \(M\) và tạo với \(\left( \alpha \right)\) một góc \(60^\circ \).Tập hợp các đường thẳng \(d\) trong không gian là
A. mặt phẳng. B. hai đường thẳng.
C. mặt nón. D. mặt trụ.
|
Câu |
1 |
2 |
3 |
4 |
5 |
|
Đáp án |
B |
A |
D |
B |
A |
|
Câu |
6 |
7 |
8 |
9 |
10 |
|
Đáp án |
A |
D |
C |
B |
C |
|
Câu |
11 |
12 |
13 |
14 |
15 |
|
Đáp án |
D |
C |
B |
D |
B |
|
Câu |
16 |
17 |
18 |
19 |
20 |
|
Đáp án |
D |
C |
D |
C |
C |
1.
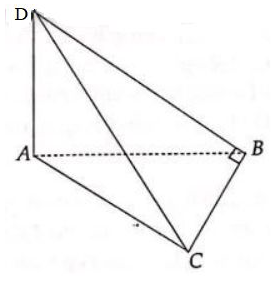
Khi quay quanh cạnh AB thì ta có một hình chóp đỉnh B, đáy là đường tròn tâm A, bán kính AD.
Tiếp tục ta có \(BD \bot BC,\,DA \bot BC \Rightarrow BC \bot AB\)
Vậy khi quay quanh AB, ta có thêm hình chóp đỉnh A đáy là đường tròn tâm B bán kính BC.
Chọn B.
2. Chiều cao của hình nón là: \(h = \sqrt {{l^2} – {r^2}} = \sqrt {{{\left( {2a} \right)}^2} – {{\left( {a\sqrt 2 } \right)}^2}} \)\(\,= a\sqrt 2 \)
Thiết diện lớn nhất đi qua S và trục của hình nón có diện tích là:
\(S = \dfrac{1}{2}h.2r = \dfrac{1}{2}a\sqrt 2 .2.a\sqrt 2 = 2{a^2}\)
Chọn A
3. Gọi hình nón có bán kính đáy là r
Đọ dài đường sinh là \(l = 2r\)
Khi đó, khai triển hình nón theo đường sinh ta được hình quạt có bán kính \(R = l = 2r\) và độ dài cung tròn là: \(L = C = 2\pi r\)
Mặt khác: \(L = \alpha R \Rightarrow \alpha = \dfrac{{2\pi r}}{{2r}} = \pi \)
Chọn D.
4.
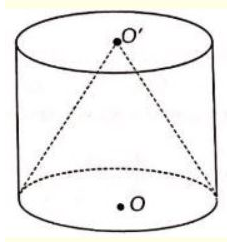
Ta có thể tích của khối trụ (H) là: \({V_1} = S.h\)
Thể tích của khối nón (N) là: \({V_2} = \dfrac{1}{3}S.h\)
\( \Rightarrow \dfrac{{{V_1}}}{{{V_2}}} = 3\) . Chọn B.
5. Thể tich khối tròn xoay tạo ra khi quay hình thang ABCD quanh trục CD là:
\(V = \dfrac{1}{3}a.\pi {a^2} + a.\pi {a^2} = \dfrac{4}{3}\pi {a^3}\)
Chọn A.
6. Độ dài đường chéo của hình vuông mặt đáy lăng trụ tứ giác đều là:
\(d = \sqrt {{{\left( {a\sqrt 2 } \right)}^2} + {{\left( {a\sqrt 2 } \right)}^2}} = 2a\)
Bán kính đường tròn đáy của hình trụ ngoại tiếp lăng trụ là: \(r = \dfrac{d}{2} = \dfrac{{2a}}{2} = a\)
Do đó thiết diện đi qua trục là 1 hình vuông.
Thể tích hình trụ là: \(V = B.h = \pi {a^2}.2a = 2\pi {a^3}\)
Do đó (I) đúng. Chọn A.
8. Gọi bán kính của khối cầu là r
Ta có diện tích đường tròn lớn là \(\pi {r^2} = 2\pi \Rightarrow r = \sqrt 2 \)
Diện tích của khối cầu đó là: \(S = 4\pi {r^2} = 4.\pi {\left( {\sqrt 2 } \right)^2} = 8\pi \)
Chọn C.
10: Ta có:
\(\begin{array}{l}{S_1} = 4\pi {R_1}^2\\{S_2} = 4\pi {R_2}^2\\ \Rightarrow \dfrac{{{S_2}}}{{{S_1}}} = \dfrac{{{R_2}^2}}{{{R_1}^2}} = {\left( {\dfrac{{{R_2}}}{{{R_1}}}} \right)^2} = {2^2} = 4\end{array}\)
Chọn C.
18:
Bán kính đáy của hình nón sẽ là: \(R = A’C’ = a\sqrt 2 \)
Đường sinh \(l = AC’ = \sqrt {A{B^2} + B{C^2} + CC{‘^2}} \)\(\, = a\sqrt 3 \)
Diện tích xung quanh của khối nón là: \({S_{xq}} = \pi Rl = \pi .a\sqrt 2 .a\sqrt 3 = \pi \sqrt 6 {a^2}\)
Chọn D.
19: Gọi r là bán kính của đường tròn đáy hình nón.
\(\begin{array}{l}{S_{xq}} = \pi rl = \pi r.8 = 240\pi \\ \Rightarrow r = 30\left( {cm} \right)\end{array}\)
Đường kính của đường tròn đáy hình nón là: \(d = 2r = 2.30 = 60\left( {cm} \right)\)
Chọn C
