
Bài 1: Cho hàm số \(y = f\left( x \right) = {x^2}.\)
a) Vẽ đồ thị của hàm số.
b) Tìm giá trị lớn nhất, nhỏ nhất của hàm số khi x thỏa mãn \(0 \le x \le 2.\)
Bài 2: Tìm giá trị của m, biết rằng hàm số \(y = \left( {1 – m} \right){x^2}\) đồng biến khi \(x > 0.\)
Bài 3: Cho hàm số \(y = \left( {m – 1} \right){x^2}\). Tìm giá trị của m biết đồ thị (P) của hàm số đi qua điểm \(A(2; − 4).\)

Advertisements (Quảng cáo)
Bài 1: a) Bảng giá trị :
|
x |
− 2 |
− 1 |
0 |
1 |
2 |
|
y |
4 |
1 |
0 |
1 |
4 |
Đồ thị của hàm số là một parabol có đỉnh là O và nhận trục Oy làm trục đối xứng.
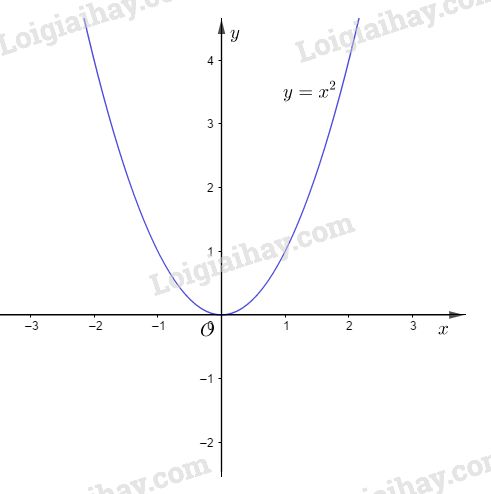
b) Ta có \(a = 1 > 0\) nên hàm số đồng biến khi \(x > 0.\)
Advertisements (Quảng cáo)
Vậy \(0 \le x \le 2 \Rightarrow f\left( 0 \right) \le f\left( x \right) \le f\left( 2 \right)\)\(\; \Rightarrow 0 \le {x^2} \le 4.\)
Vậy giá trị nhỏ nhất của hàm số bằng 0, khi \(x = 0\); giá trị lớn nhất của hàm số bằng 4, khi \(x = 2.\)
Bài 2: Hàm số đồng biến khi \(x > 0 \Leftrightarrow 1 – m > 0 \Leftrightarrow m < 1.\)
Bài 3: Ta có \(A \in (P) \Rightarrow – 4 = \left( {m – 1} \right){.2^2} \)
\(\;\Rightarrow m – 1 = – 1 \Rightarrow m = 0.\)

![[Phòng GD Gò Dầu] kiểm tra cuối năm môn Văn lớp 9 năm 2020: hân tích khổ thơ thứ 4,5 trong bài thơ “Mùa xuân nho nhỏ” của nhà thơ Thanh Hải](https://dethikiemtra.com/wp-content/uploads/2020/09/anh-dep-ve-thay-co-1-100x75.jpg)




