
Bài 1: Cho đồ thị hai hàm số \(y = {x^2}\) (P) và \(y = 2x \) (d). Tìm tọa độ giao điểm của (P) và (d).
Bài 2: Cho hàm số \(y = – {1 \over 4}{x^2}.\) Biết rằng điểm \(M(m; − 1)\) thuộc đồ thị của hàm số. Tìm m.
Bài 3: a) Vẽ đồ thị của hàm số \(y = 2{x^2}.\)
b) Với giá trị nào của m thì đường thẳng \(y = m\) không cắt đồ thị của hàm số \(y = 2{x^2}.\)

Bài 1: Phương trình hoành độ giao điểm của (P) và (d) :
Advertisements (Quảng cáo)
\({x^2} = 2x \Leftrightarrow {x^2} – 2x = 0 \)
\(\Leftrightarrow x\left( {x – 2} \right) = 0 \)
\(\Leftrightarrow \left[ \matrix{ x = 0 \hfill \cr x = 2 \hfill \cr} \right.\)
Ta có các giao điểm : \(O(0; 0)\) và \(M(2; 4)\).
Advertisements (Quảng cáo)
Bài 2: \(M(m; − 1)\) thuộc đồ thị nên \( – 1 = – {1 \over 4}{m^2} \Leftrightarrow {m^2} = 4 \Leftrightarrow m = \pm 2.\)
Bài 3: a) Bảng giá trị :
|
x |
− 1 |
\( – {1 \over 2}\) |
0 |
\({1 \over 2}\) |
1 |
|
y |
2 |
\({1 \over 2}\) |
0 |
\({1 \over 2}\) |
2 |
Đồ thị của hàm số là parabol có đỉnh là O và nhận trục Oy làm trục đối xứng.
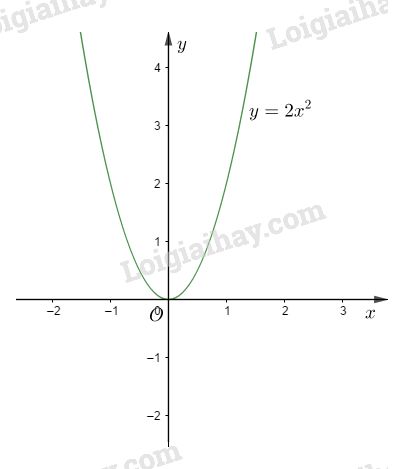
b) Đồ thị (P) của hàm số \(y = 2{x^2}\) nằm phía trên của trục \(Ox\). Đường thẳng (d): \(y = m\) là đường thẳng song song với trục \(Ox\). Vậy \(m < 0\) thì (d) và (P) không cắt nhau.





