Đáp án và hướng dẫn giải Bài 1,2,3 SGK trang 28 giải tích lớp 11 (Bài tập phương trình lượng giác cơ bản) Chương 1 giải tích lớp 11.
Bài 1: Giải các phương trình sau:
a) sin (x + 2) = 1/3
b) sin 3x = 1 ;
c) sin (2x/3-π/3) = 0
d) sin (2x + 200) = (-√3)/2
Giải: a) sin (x + 2) = 1/3


b) sin 3x = 1 ⇔ 3x = π/2 + k2π
⇔ x = π/6 + k(2π/3) , (k ∈ Z).
c) sin (2x/3-π/3)=0
⇔ 2x/3-π/3 =kπ
⇔ x = π/2 +k(3π/2) , (k ∈ Z).
Advertisements (Quảng cáo)
d) Vì -√3/2 = sin(-600) nên pt đã cho tương đương với
sin (2x +200) = sin(-600)
⇔  ⇔
⇔ 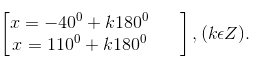
Bài 2: Với những giá trị nào của x thì giá trị của các hàm số y = sin3x và y = sinx bằng nhau?
Giải: x thỏa mãn yêu cầu bài ra khi và chỉ khi
⇔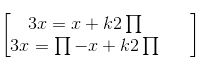
⇔
Advertisements (Quảng cáo)
Bài 3: Giải các phương trình sau:
a) cos (x – 1) = 2/3 ;
b) cos 3x = cos 120 ;
c) cos (3x/2 – π/4) = -1/2 ;
d) cos22x =1/4

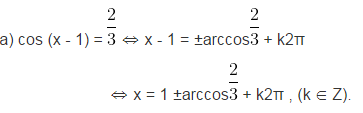
![]()

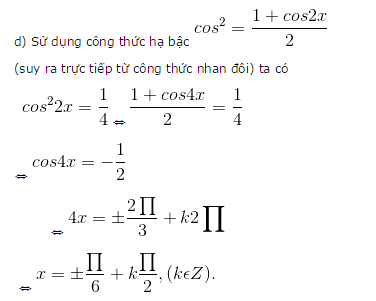
Ôn lại Lý thuyết
1. Phương trình cơ bản
Lưu ý: Nếu trong đề toán đã ngầm quy định ẩn số được tính bằng đơn vị đo nào thì khi viết công thức nghiệm các em nhất thiết phải dùng đúng đơn vị đo đó. Chẳng hạn, khi đề toán là giải pt cos(x + 450) = -0,5 thì đã ngầm yêu cầu tính số đo bằng độ của cung x thỏa mãn pt đã cho. Trong trường hợp đó, trong công thức nghiệm, thay cho π ta phải viết là 1800 .
2. Sử dụng máy tính bỏ túi
Vài năm trước đây, khi biên soạn SGK theo chương trình mới, các tác giả còn e ngại việc sử dụng máy tính bỏ túi chưa phổ biến trong học sinh. Tuy nhiên, đất nước đổi mới và hội nhập với thế giới đã làm tình hình thay đổi nhanh chóng : đa số học sinh phổ thông đã có và sử dụng máy tính bỏ túi như một dụng cụ học tập bình thường. Biết sử dụng máy tính bỏ túi, việc thực hiện rất nhiều tính toán trở nên nhanh chóng, nhẹ nhàng và đặc biệt giúp học sinh bớt phải nhớ nhiều kiến thức (chẳng hạn trong tính toán xác suất thống kê, giải pt, bất pt, … ). Hiện nay học sinh thường sử dụng máy CASIO fx-500 MS, CASIO fx-570 MS, CASIO fx-570 ES nên dưới đây chúng tôi sẽ giới thiệu cách sử dụng cả ba loại máy tính này.
Chú ý :
-
- Nếu máy tính đang trong chế độ tính toán thì có thể bỏ qua bước thứ nhất (vào chế độ tính toán). Tương tự, nếu máy tính đang trong chế độ sử dụng đơn vị radian thì có thể bỏ qua bước thứ hai (sử dụng đơn vị radian), … .
- Máy tính không có chức năng tìm arccot vì nếu a > 0 thì arccota = arccota-1 , còn nếu a < 0 thì arccota = π + arccota-1 .






