Tóm tắt lý thuyết và giải bài tập bài 1,2,3,4 trang 7 SGK Hình học 10: Các Định nghĩa – Chương 1 Véc tơ.
A. Tóm tắt lý thuyết
1. Định nghĩa
– Vectơ là một đoạn thẳng định hướng.
– Vectơ có điểm đầu là A, điểm cuối B là vectơ AB, kí hiệu ![]() Khi không cần chỉ rõ điểm đầu, điểm cuối vectơ còn được kí hiệu
Khi không cần chỉ rõ điểm đầu, điểm cuối vectơ còn được kí hiệu ![]() …
…
– Đường thẳng đi qua điểm đầu và điểm cuối của vectơ gọi là giá của vectơ.
2. Vec tơ cùng phương, vectơ cùng hướng.
– Hai vec tơ cùng phương nếu giá của chúng song song hoặc trùng nhau.
– Hai vectơ cùng phương thì có thể cùng hướng hoặc ngược hướng nếu chúng cùng phương.
3. Hai vectơ bằng nhau
– Độ dài của vectơ là khoảng cách giữa điểm đầu và điểm cuối của nó hay nói gọn hơn, độ dài của vectơ ![]() là độ dài đoạn thẳng AB, kí hiệu
là độ dài đoạn thẳng AB, kí hiệu ![]()
![]() Độ dài vectơ là một số không âm.
Độ dài vectơ là một số không âm.
Véc tơ có độ dài bằng 1 gọi là vectơ đơn vị.
– Hai vectơ bằng nhau nếu chúng cùng hướng và có cùng độ dài.
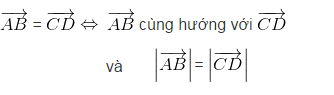 – Khi cho trước một vectơ
– Khi cho trước một vectơ ![]() và một vectơ 0 trong mặt phẳng, ta luôn tìm được một điểm A để có
và một vectơ 0 trong mặt phẳng, ta luôn tìm được một điểm A để có ![]()
Điểm A như vậy là duy nhất.
Advertisements (Quảng cáo)
4. Vec tơ- không
Vectơ- không kí hiệu là ![]() là vectơ có điểm đầu và điểm cuối trùng nhau:
là vectơ có điểm đầu và điểm cuối trùng nhau: ![]()
Vectơ- không có độ dài bằng 0 và hướng tùy ý
B. Hướng dẫn giải bài tập SGK trang 7 hình học lớp 10
Bài 1. Cho ba vectơ a,b,c đều khác vec tơ 0. Các khẳng định sau đây đúng hay sai?

Hướng dẫn bài 1: a) Gọi theo thứ tự ∆1, ∆2, ∆3 là giá của các vectơ ![]()
![]() ⇒ ∆1 //∆3 ( hoặc ∆1 = ∆3 ) (1)
⇒ ∆1 //∆3 ( hoặc ∆1 = ∆3 ) (1)
![]() ⇒ ∆2 // ∆3 ( hoặc ∆2 = ∆3 ) (2)
⇒ ∆2 // ∆3 ( hoặc ∆2 = ∆3 ) (2)
Advertisements (Quảng cáo)
Từ (1), (2) suy ra ∆1 // ∆2 ( hoặc ∆1 = ∆2 ), theo định nghĩa hai vectơ a,b cùng phương.
Vậy câu a) đúng.
b) Đúng.
Bài 2. Trong hình 1.4, hãy chỉ ra các vec tơ cùng phương, cùng hướng, ngược hướng và các vectơ bằng nhau.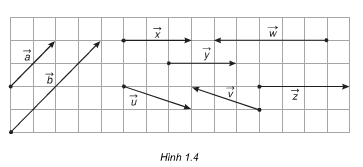
Giải: – Các vectơ cùng phương: ![]() – Các vectơ cùng hướng:
– Các vectơ cùng hướng: ![]() – Các vectơ ngược hướng:
– Các vectơ ngược hướng: ![]() – Các vectơ bằng nhau:
– Các vectơ bằng nhau: ![]()
Bài 3. Cho tứ giác ABCD. Chứng minh rằng tứ giác đó là hình bình hành khi và chỉ khi ![]()
Giải: Ta chứng minh hai mệnh đề:
– Khi ![]() thì ABCD là hình bình hành.
thì ABCD là hình bình hành.
Thật vậy, theo định nghĩa của vec tơ bằng nhau thì:
![]()

=> ![]()
![]() suy ra giá của chúng song song với nhau, hay AB // DC (1)
suy ra giá của chúng song song với nhau, hay AB // DC (1)
Ta lại có ![]() ⇒ AB = DC (2)
⇒ AB = DC (2)
Từ (1) và (2), theo dấu hiệu nhận biết hình bình hành, tứ giác ABCD có một cặp cạnh song song và bằng nhau nên nó là hình bình hành.
– Khi ABCD là hình bình hành thì ![]() Khi ABCD là hình bình hành thì AB // CD. Dễ thấy, từ đây ta suy ra hai vec tơ
Khi ABCD là hình bình hành thì AB // CD. Dễ thấy, từ đây ta suy ra hai vec tơ ![]()
Mặt khác AB = CD ⇒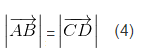 Từ (3) và (4) suy ra
Từ (3) và (4) suy ra ![]()
Bài 4. Cho lục giác đều ABCDEF có tâm o.
a) Tìm các véc tơ khác véc tơ 0 và cùng phương với véc tơ OA
b) Tìm các véc tơ bằng véc tơ AB
Hướng dẫn :
a) Các vec tơ cùng phương với vec tơ OA

b) Các véc tơ bằng véc tơ AB; ![]()






