
1. Cho tam giác ABC vuông tại B có trọng tâm là G. Biết rằng \(AB = 3\) và \(AC = 5\). Tính độ dài của các véctơ \(\overrightarrow {GB} – \overrightarrow {GC} \) và \(\overrightarrow {GB} + \overrightarrow {GC} \).
2. Cho tam giác ABC có trọng tâm G. Gọi E và F là các điểm xác định bởi \(\overrightarrow {AE} = 2\overrightarrow {AB} \) và \(\overrightarrow {AF} = \dfrac{2 }{ 5}\overrightarrow {AC} \)
a.Hãy biểu diễn các véctơ \(\overrightarrow {GE} \) và \(\overrightarrow {GF} \)theo các véctơ \(\overrightarrow {AB} \) và \(\overrightarrow {AC} \).
b.Chứng minh ba điểm G, E, F thẳng hàng.
3. Cho tam giác ABC và một đường thẳng \(\Delta \). Tìm trên \(\Delta \) điểm M sao cho véctơ \(2\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} \)có độ dài ngắn nhất.

1.
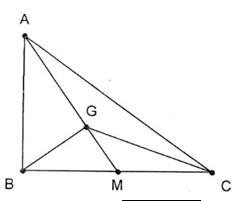
Theo Pitago \(BC = \sqrt {A{C^2} – A{B^2}} = \sqrt {25 – 9} = 4.\)
Gọi M là trung điểm BC. Khi đó \(AM = \sqrt {A{B^2} + B{M^2}} = \sqrt {9 + 4} \)\(\, = \sqrt {13} \) .
Advertisements (Quảng cáo)
Ta có \(\overrightarrow {GB} – \overrightarrow {GC} = \overrightarrow {CB} .\) Suy ra \(\left| {\overrightarrow {GB} – \overrightarrow {GC} } \right| = \left| {\overrightarrow {CB} } \right| = CB = 4\) .
Tương tự \(\overrightarrow {GB} + \overrightarrow {GC} = 2\overrightarrow {GM} \) .
Suy ra \(\left| {\overrightarrow {GB} + \overrightarrow {GC} } \right| = \left| {2\overrightarrow {GM} } \right| = 2GM\)\(\, = \dfrac{2 }{3}AM = \dfrac{2\sqrt {13} } { 3}\) .
2.
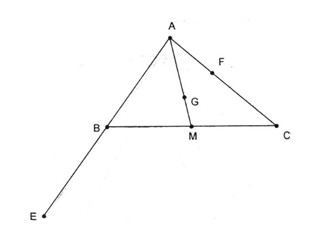
a.Ta có
Advertisements (Quảng cáo)
\(\eqalign{ & \overrightarrow {GE} = \overrightarrow {AE} – \overrightarrow {AG} \cr&\;\;\;\;\;\;\;= 2\overrightarrow {AB} – {2 \over 3}\overrightarrow {AM} \cr & \;\;\;\;\;\;\;= 2\overrightarrow {AB} – {1 \over 3}\left( {\overrightarrow {AB} + \overrightarrow {AC} } \right)\cr& \;\;\;\;\;\;\;= {5 \over 3}\overrightarrow {AM} – {1 \over 3}\overrightarrow {AC} \cr} \)
\(\eqalign{ & \overrightarrow {GF} = \overrightarrow {AF} – \overrightarrow {AG} \cr&\;\;\;\;\;\;\;= {2 \over 5}\overrightarrow {AC} – {2 \over 3}\overrightarrow {AM} \cr & \;\;\;\;\;\;\; = {2 \over 5}\overrightarrow {AC} – {1 \over 3}\left( {\overrightarrow {AB} + \overrightarrow {AC} } \right)\cr&\;\;\;\;\;\;\; = – {1 \over 3}\overrightarrow {AM} + {1 \over {15}}\overrightarrow {AC} \cr} \)
b. Ta có \(\overrightarrow {GE} = – 5\overrightarrow {GF} \) . Suy ra \(\overrightarrow {GE} \) và \(\overrightarrow {GF} \) cùng phương nên G, E, F thẳng hàng.
3.
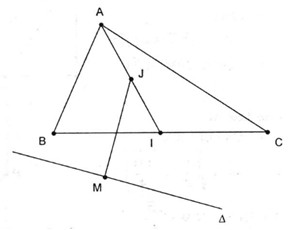
Gọi I là trung điểm BC và J là trung điểm AI.
Ta có
\(2\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} \)
\(= 2\overrightarrow {MA} + 2\overrightarrow {MI} \)
\(= 2\left( {\overrightarrow {MA} + \overrightarrow {MI} } \right) = 4\overrightarrow {MJ} \)
Do đó \(\left| {2\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} } \right|\)\(\, = \left| {4\overrightarrow {MJ} } \right| = 4MJ\)
Suy ra \(2\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} \) có độ dài ngắn nhất khi và chỉ khi 4MJ ngắn nhất. Điều này xảy ra khi M là hình chiếu của J trên \(\Delta \) .

