
Chọn phương án đúng
1. Cho tam giác ABC với M, N, P lần lượt là trung điểm của các cạnh AB, AC, BC. Véc tơ đối của véc tơ \(\overrightarrow {MN} \)là
A.\(\overrightarrow {BP} \)
B.\(\overrightarrow {MA} \)
C.\(\overrightarrow {PC} \)
D.\(\overrightarrow {PB} \)
2. Cho ba điểm A, B, C phân biệt. Đẳng thức nào sau đây là sai ?
A.\(\overrightarrow {AB} – \overrightarrow {BC} = \overrightarrow {AC} \)
B.\(\overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow {AC} \)
C.\(\overrightarrow {BC} + \overrightarrow {AB} = \overrightarrow {AC} \)
D.\(\overrightarrow {BC} – \overrightarrow {BA} = \overrightarrow {AC} \)
3. Cho hình bình hành ABCD có tâm O. Khi đó ta có
A.\(\overrightarrow {AO} – \overrightarrow {BO} = \overrightarrow {BA} \)
B.\(\overrightarrow {OA} – \overrightarrow {OB} = \overrightarrow {BA} \)
C.\(\overrightarrow {OA} – \overrightarrow {OB} = \overrightarrow {AB} \)
D.\(\overrightarrow {AO} + \overrightarrow {BO} = \overrightarrow {AB} \)
4. Cho hình vuông ABCD. Khi đó ta có
A.\(\overrightarrow {AB} = – \overrightarrow {BC} \)
B.\(\overrightarrow {AD} = – \overrightarrow {BC} \)
C.\(\overrightarrow {AC} = – \overrightarrow {BD} \)
D.\(\overrightarrow {AD} = – \overrightarrow {CB} \)
5. Cho hai điểm phân biệt M, N. Điều kiện cần và đủ để P là trung điểm của đoạn MN là
A\(\overrightarrow {PM} = – \overrightarrow {PN} \)
B.\( PM=PN\)
C.\(\overrightarrow {PM} = \overrightarrow {PN} \)
D.\(\overrightarrow {MP} = \overrightarrow {NP} \)
6. Cho G là trọng tâm của tam giác ABC và M là trung điểm của đoạn BC. Đẳng thức nào sau đây sai ?
A.\(\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} = \overrightarrow 0 \)
Advertisements (Quảng cáo)
B.\(\overrightarrow {AB} + \overrightarrow {AC} = 2\overrightarrow {AM} \)
C.\(\overrightarrow {GB} + \overrightarrow {GC} = 2\overrightarrow {GM} \)
D.\(\overrightarrow {BM} + \overrightarrow {MC} = \overrightarrow 0 \)
7. Gọi I là giao điểm của hai đường chéo của hình bình hành ABCD. Khi đó
A.\(\overrightarrow {AI} = \dfrac{1 }{ 2}\overrightarrow {AB} + \dfrac{1 }{ 2}\overrightarrow {AC} \)
B.\(\overrightarrow {AI} = \dfrac{1 }{3}\overrightarrow {AB} + \dfrac{1 }{3}\overrightarrow {AD} \)
C.\(\overrightarrow {AI} = \dfrac{1 }{2}\overrightarrow {AB} + \dfrac{1 }{ 2}\overrightarrow {AD} \)
D.\(\overrightarrow {AI} = \dfrac{1 }{ 2}\overrightarrow {AB} + \overrightarrow {BI} \)
8. Cho tam giác ABC. Gọi M là điểm trên đoạn BC sao cho MB = 2MC.
Khi đó
A.\(\overrightarrow {AM} = dfrac{1 }{ 3}\overrightarrow {AB} + \overrightarrow {AC} \)
B.\(\overrightarrow {AM} = \dfrac{1 }{3}\overrightarrow {AB} + \dfrac{2 }{ 3}\overrightarrow {AC} \)
C.\(\overrightarrow {AM} = \dfrac{1 }{3}\overrightarrow {AB} + \dfrac{1 }{ 3}\overrightarrow {AC} \)
D.\(\overrightarrow {AM} = \dfrac{1 }{3}\overrightarrow {AB} + 2\overrightarrow {AC} \)
9. Cho tam giác đều ABC có cạnh bằng a, M là trung điểm của BC. Véc tơ \(\overrightarrow {CA} – \overrightarrow {MC} \) có độ lớn là
A.\(\dfrac{{3a}}{2}\)
B. \(\dfrac{a}{2}\)
C. \(\dfrac{{2a\sqrt 3 }}{3}\)
Advertisements (Quảng cáo)
D. \(\dfrac{{a\sqrt 7 }}{2}\)
1.0. Cho tam giác ABC vuông tại B có AB = 3cm, BC = 4cm. Độ dài của véctơ tổng \(\overrightarrow {AB} + \overrightarrow {AC} \) là
A.\(\sqrt {13} \)cm
B. \(13\) cm
C. \(2\sqrt {13} \) cm
D. \(26\) cm

1..D

Véctơ đối của véctơ \(\overrightarrow {MN} \) là véctơ \(\overrightarrow {PB} \) .
2..A. Ta có \(\overrightarrow {AB} – \overrightarrow {AC} = \overrightarrow {CB} \)
\(\Rightarrow \overrightarrow {AC} = \overrightarrow {AB} – \overrightarrow {CB} \ne \overrightarrow {AB} – \overrightarrow {BC} \)
3..B
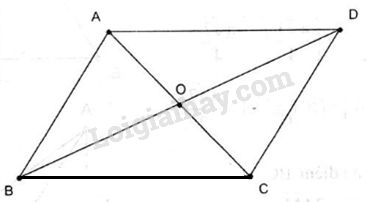
Theo quy tắc của phép trừ ta có \(\overrightarrow {OB} – \overrightarrow {OA} = \overrightarrow {AB} \) .
5..A. Ta có P là trung điểm \(MN \Leftrightarrow \overrightarrow {PM} + \overrightarrow {PN} = 0 \)
\(\Leftrightarrow \overrightarrow {PM} = – \overrightarrow {PN} \) .
6..D
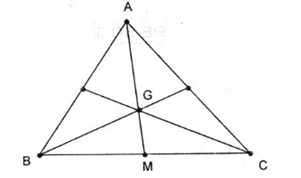
Ta có \(\overrightarrow {BM} + \overrightarrow {MC} = \overrightarrow {BC} \ne \overrightarrow 0 \) .
7..C
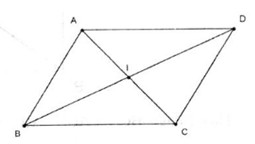
Ta có: \(\overrightarrow {AB} + \overrightarrow {AD} = 2\overrightarrow {AI} = \dfrac{1 }{ 2}\overrightarrow {AB} + \dfrac{1 }{ 2}\overrightarrow {AD} \) .
8..B
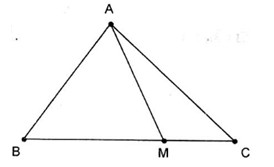
Ta có \(\overrightarrow {BM} = \overrightarrow {AM} – \overrightarrow {AB} ,\) \({\rm{ }}\overrightarrow {CM} = \overrightarrow {AM} – \overrightarrow {AC} \).
Mà \(\overrightarrow {BM} = – 2\overrightarrow {CM} \) .
Suy ra \(\overrightarrow {AM} – \overrightarrow {AB} = – 2\left( {\overrightarrow {AM} – \overrightarrow {AC} } \right)\) .
\( \Rightarrow 3\overrightarrow {AM} = \overrightarrow {AB} + 2\overrightarrow {AC} \)
\( \Rightarrow \overrightarrow {AM} = \dfrac{1 }{ 3}\overrightarrow {AB} +\dfrac{2 }{3}\overrightarrow {AC} \)
9.. D
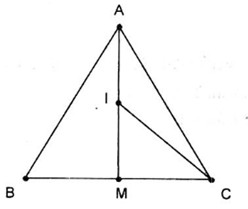
Gọi I là trung điểm AM. Ta có \(\overrightarrow {CA} – \overrightarrow {MC} = \overrightarrow {CA} + \overrightarrow {CM} = 2\overrightarrow {CI} .\)
\(\eqalign{
& CI = \sqrt {C{M^2} + M{I^2}} \cr
& \,\,\,\,\,\,\,\,\,\, = \sqrt {{{\left( {\frac{a}{2}} \right)}^2} + {{\left( {\frac{{a\sqrt 3 }}{4}} \right)}^2}} \cr
& \,\,\,\,\,\,\,\,\,\,= \frac{{a\sqrt 7 }}{2}. \cr} \)
Vậy \(\left| {\overrightarrow {CA} – \overrightarrow {MC} } \right| = \left| {\overrightarrow {CI} } \right| = 2CI = {{a\sqrt 7 } \over 2}.\)
1.0. C
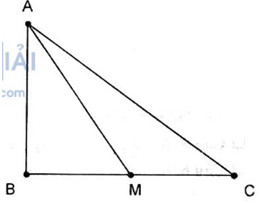
Gọi M là trung điểm BC. Ta có \(\overrightarrow {AB} + \overrightarrow {AC} = 2\overrightarrow {AM} \) .
Mà \(AM = \sqrt {A{B^2} + B{M^2}} \)\(\, = \sqrt {9 + 4} = \sqrt {13} \) cm.
Vậy \(\left| {\overrightarrow {AB} + \overrightarrow {AC} } \right| = \left| {2\overrightarrow {AM} } \right| \)\(\,= 2AM = 2\sqrt {13} \) cm.

