Kiểm tra 15 phút môn Toán lớp 9 Chương 3 Hình học: Chứng minh rằng AB.CD = AD.CE

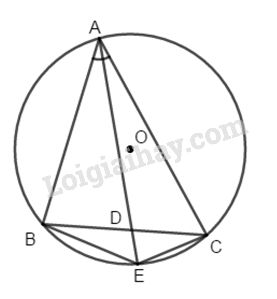
Cho ∆ABC ( AB < AC) nội tiếp trong đường tròn (O). Lấy D trên cạnh BC, AD cắt cung BC ở E. Chứng minh rằng :

a)\(\widehat {AEC} > \widehat {AEB}\)

b) \(AB. CD = AD . CE\)

a) Ta có\(\widehat {AEC} = \widehat {ABC}\) ( góc nội tiếp cùng chắn cung AC) và\(\widehat {AEB} = \widehat {ACB}\) ( góc nội tiếp cùng chắn cung AB) mà \(\widehat {ABC} > \widehat {ACB}\) ( vì \(AB < AC\))

Do đó \(\widehat {AEC} > \widehat {AEB}\).

b) Xét ∆ABD và ∆CED có :

+) \(\widehat {ABD} > \widehat {DEC}\) (cmt)

+) \(\widehat {BAE} = \widehat {BCE}\) ( góc nội tiếp cùng chắn cung BE)

Vậy ∆ABD đồng dạng với ∆CED (g.g)

\(\Rightarrow \dfrac{{AB}}{ {CE}} = \dfrac{{AD} }{{CD}}\)

\(\Rightarrow AB. CD = AD . CE\).