
Bài 1. Không dùng bảng số và máy tính, hãy sắp xếp các tỉ số lượng giác sau đây theo thứ tự giảm dần : sin25˚; cos35˚; sin50˚; cos70˚.
Bài 2. Cho ∆ABC vuông tại A, biết \(\tan B = {3 \over 4}\). Hãy tính các tỉ số lượng giác của góc C.

Bài 1. Ta có:
\(\eqalign{ & \cos 35^\circ = \sin \left( {90^\circ – 35^\circ } \right) = \sin 55^\circ \cr & \cos 70^\circ = \sin \left( {90^\circ – 70^\circ } \right) = \sin 20^\circ . \cr} \)
Mà \(\sin 55^\circ > \sin 50^\circ > \sin 25^\circ > \sin 20^\circ \)
\( \Rightarrow \cos 35^\circ > \sin 50^\circ > \sin 25^\circ \)\(\,> \cos 70^\circ \)
Advertisements (Quảng cáo)
Bài 2.
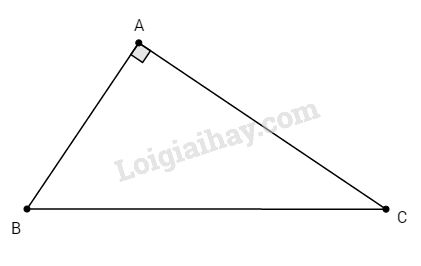
Ta có:
\(\eqalign{ & \tan B = {{AC} \over {AB}} = {3 \over 4} \Rightarrow {{AC} \over 3} = {{AB} \over 4} \cr & \Rightarrow {{A{C^2}} \over 9} = {{A{B^2}} \over {16}} = {{A{C^2} + A{B^2}} \over {9 + 16}}\cr&\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; = {{B{C^2}} \over {25}} \cr & \Rightarrow {{A{C^2}} \over {B{C^2}}} = {9 \over {25}}\,\text{ và }\,{{A{B^2}} \over {B{C^2}}} = {{16} \over {25}} \cr} \)
Advertisements (Quảng cáo)
Theo định nghĩa :
\(\eqalign{ & \sin B = {{AC} \over {BC}} \cr&\Rightarrow {\sin ^2}B = {{A{C^2}} \over {B{C^2}}} = {9 \over {25}} \cr & \Rightarrow \sin B = {3 \over 5}. \cr} \)
Do đó: \(\cos C = {3 \over 5}\)
Tương tự:
\(\eqalign{ & \cos B = {{AB} \over {BC}} \cr& \Rightarrow {\cos ^2}B = {{A{B^2}} \over {B{C^2}}} = {{16} \over {25}} \cr & \Rightarrow \cos B = {4 \over 5}. \cr} \)
Do đó: \(\sin C = {4 \over 5}\)
Vì \(\tan B = {4 \over 5} \Rightarrow \cot C = {3 \over 4} \Rightarrow \tan C = {4 \over 3}\)





